For each alkane,
1. draw all the possible monochlorinated derivatives.
c. 2-methylpentane
d. 2,2,3,3-tetramethyl butane
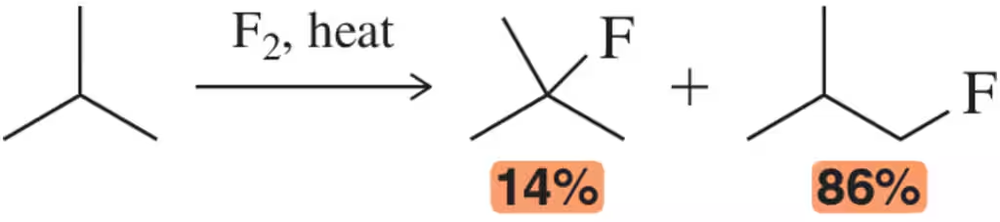
 Verified step by step guidance
Verified step by step guidance Verified video answer for a similar problem:
Verified video answer for a similar problem:

 2:05m
2:05mMaster The one reaction that alkanes will actually undergo. with a bite sized video explanation from Johnny
Start learning