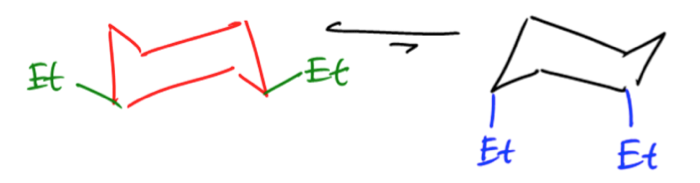
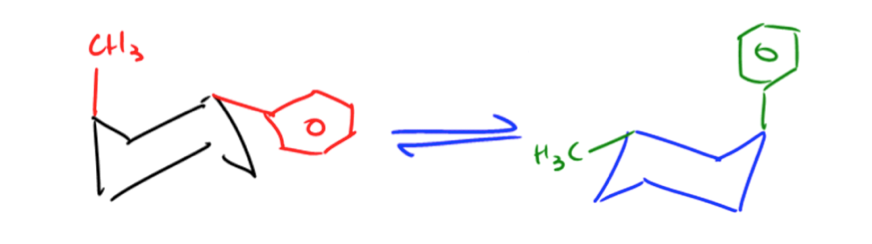
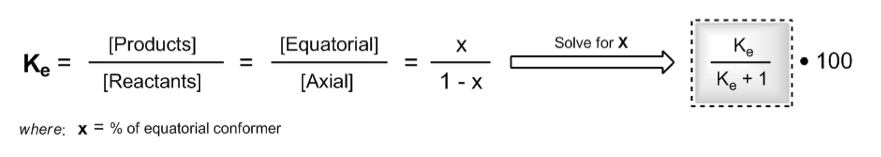Understanding the relationship between free energy and molecular conformations is crucial in chemistry, particularly when analyzing cyclohexane. The Gibbs free energy equation plays a pivotal role in determining the equilibrium constant, which in turn allows us to calculate the exact percentages of different conformations at a given temperature.
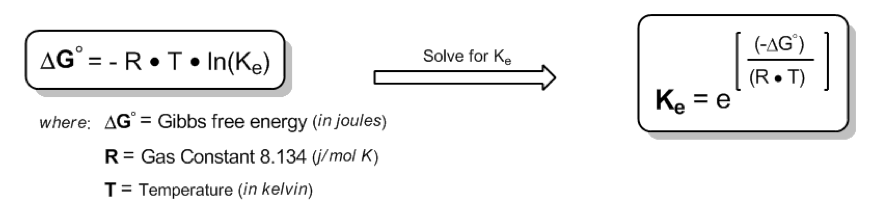
The Gibbs free energy change (\( \Delta G \)) is expressed as:
\[ \Delta G = -RT \ln(K_E) \]
In this equation, \( R \) is the gas constant, specifically \( 8.314 \, \text{J/mol·K} \), and \( T \) is the temperature in Kelvin. Remember that to convert Celsius to Kelvin, you add 273.15. The equilibrium constant (\( K_E \)) is defined as the ratio of products to reactants at equilibrium, which is essential for calculating the percentages of conformations.
To find \( K_E \), we rearrange the equation to:
\[ K_E = e^{-\Delta G / (RT)} \]
Here, \( \Delta G \) is derived from the energy difference between axial and equatorial conformations, where we input the positive value of \( \Delta G \) to reflect the energy required to transition to the less stable axial form.
When \( K_E \) is greater than 1, it indicates that the products (more stable equatorial conformation) are favored over the reactants (less stable axial conformation). The relationship can be expressed as:
\[ K_E = \frac{X}{1 - X} \]
Where \( X \) represents the fraction of the more stable conformation. Solving for \( X \) gives:
\[ X = \frac{K_E}{K_E + 1} \]
To express this as a percentage, multiply by 100:
\[ \text{Percentage of equatorial conformation} = X \times 100 \]
Consequently, the percentage of the axial conformation can be calculated as \( 100 - \text{Percentage of equatorial} \).
While the derivation and application of these equations may seem complex, the key takeaway is to familiarize yourself with the Gibbs free energy equation and the equilibrium constant definition. Mastery of these concepts will enable you to accurately determine the conformational percentages of cyclohexane and similar compounds in your studies.