For each pair, give the relationship between the two compounds. Making models will be helpful.
(g)
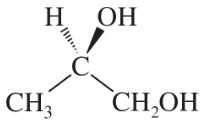
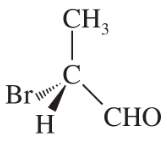
 Verified step by step guidance
Verified step by step guidance Verified video answer for a similar problem:
Verified video answer for a similar problem: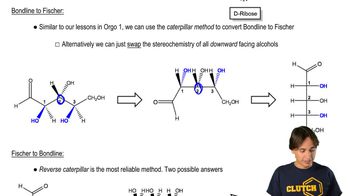
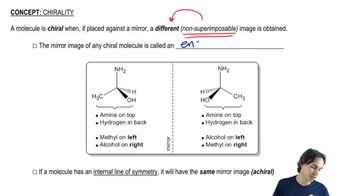


 1:15m
1:15mMaster Introduction to different projections. with a bite sized video explanation from Johnny
Start learning