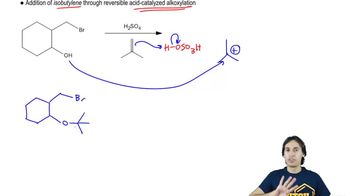
In Chapter 13, we discuss the ring-opening reactions of epoxides, such as the one shown here.
(b) Predict the sign of ∆S°.
 Verified step by step guidance
Verified step by step guidance Verified video answer for a similar problem:
Verified video answer for a similar problem:


 2:46m
2:46mMaster Explaining what entropy is. with a bite sized video explanation from Johnny
Start learning