A marketing manager wants to evaluate whether three different advertising platforms-TV, social media, and print media-lead to different average sales performance across regional stores. She runs a 4-wook advertising campaign, assigning one platform to a group of 5 stores each (15 stores total). After the campaign, she collects the weekly soles (in \$1,000s) for each store during the campaign period. She wants to determine whether there is a statistically significant difference in mean sales among the three advertising platforms. In an ANOVA test a P-value of 0.03 is obtained. What can be concluded about mean weekly sales for different advertising platforms?
Table of contents
- 1. Introduction to Statistics53m
- 2. Describing Data with Tables and Graphs2h 1m
- 3. Describing Data Numerically2h 8m
- 4. Probability2h 26m
- 5. Binomial Distribution & Discrete Random Variables3h 28m
- 6. Normal Distribution & Continuous Random Variables2h 21m
- 7. Sampling Distributions & Confidence Intervals: Mean3h 37m
- Sampling Distribution of the Sample Mean and Central Limit Theorem19m
- Distribution of Sample Mean - Excel23m
- Introduction to Confidence Intervals22m
- Confidence Intervals for Population Mean1h 26m
- Determining the Minimum Sample Size Required12m
- Finding Probabilities and T Critical Values - Excel28m
- Confidence Intervals for Population Means - Excel25m
- 8. Sampling Distributions & Confidence Intervals: Proportion1h 33m
- 9. Hypothesis Testing for One Sample3h 32m
- 10. Hypothesis Testing for Two Samples4h 49m
- Two Proportions1h 12m
- Two Proportions Hypothesis Test - Excel28m
- Two Means - Unknown, Unequal Variance1h 2m
- Two Means - Unknown Variances Hypothesis Test - Excel12m
- Two Means - Unknown, Equal Variance15m
- Two Means - Unknown, Equal Variances Hypothesis Test - Excel9m
- Two Means - Known Variance12m
- Two Means - Sigma Known Hypothesis Test - Excel21m
- Two Means - Matched Pairs (Dependent Samples)42m
- Matched Pairs Hypothesis Test - Excel12m
- 11. Correlation1h 24m
- 12. Regression1h 59m
- 13. Chi-Square Tests & Goodness of Fit2h 31m
- 14. ANOVA2h 1m
14. ANOVA
Introduction to ANOVA
Struggling with Statistics for Business?
Join thousands of students who trust us to help them ace their exams!Watch the first videoMultiple Choice
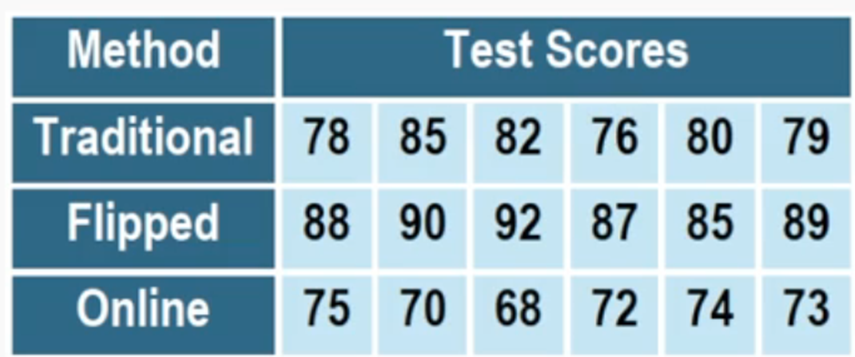
A school administrator wants to examine whether students' academic performance differs based on the type of instructional method used in their classes. A random sample of 18 students is selected and divided evenly among the three teaching methods. After a semester, all students take the same standardized final exam. State the null and alternative hypotheses for a one-way ANOVA test.
A
H0: All means are the same
HA: At least one mean is different, at least one method has a different average test score.
B
H0: All students perform equally well on the final exam, regardless of the instructional method.
H1: At least one group of students performs differently than the others.
C
H0: The three instructional methods lead to different mean exam scores.
H1: All three instructional methods lead to the same mean exam scores.
D
H0: There is a significant difference among the teaching methods.
H1: There is no significant difference among the teaching methods.
 Verified step by step guidance
Verified step by step guidance1
Step 1: Understand the context of the problem. The school administrator wants to determine if students' academic performance differs based on the type of instructional method (Traditional, Flipped, Online). This requires comparing the mean test scores of the three groups using a one-way ANOVA test.
Step 2: Define the null hypothesis (H₀) and the alternative hypothesis (H₁). For a one-way ANOVA test: H₀: All group means are equal (students perform equally well regardless of instructional method). H₁: At least one group mean is different (at least one instructional method leads to different average test scores).
Step 3: Organize the data provided in the table. The test scores for each instructional method are: Traditional: [78, 85, 82, 76, 80, 79], Flipped: [88, 90, 92, 87, 85, 89], Online: [75, 70, 68, 72, 74, 73]. These scores will be used to calculate the group means and variances.
Step 4: Perform the one-way ANOVA test. Calculate the following: (a) The mean test score for each group, (b) The overall mean test score, (c) The between-group variance (how much the group means differ from the overall mean), and (d) The within-group variance (how much individual scores differ within each group).
Step 5: Compare the F-statistic (calculated from the ANOVA test) to the critical value from the F-distribution table at the chosen significance level (e.g., α = 0.05). If the F-statistic exceeds the critical value, reject the null hypothesis (H₀) and conclude that at least one group mean is significantly different.

 6:46m
6:46mWatch next
Master Introduction to ANOVA with a bite sized video explanation from Patrick
Start learningRelated Videos
Related Practice
Multiple Choice
Introduction to ANOVA practice set


