Probabilities & Z-Scores w/ Graphing Calculator: Videos & Practice Problems

In statistical analysis, understanding how to find probabilities associated with z-scores is crucial, especially when dealing with normal distributions. A z-score represents the number of standard deviations a data point is from the mean. To find probabilities from z-scores, one can utilize a z-table or a graphing calculator, such as the TI-84, which simplifies the process significantly.

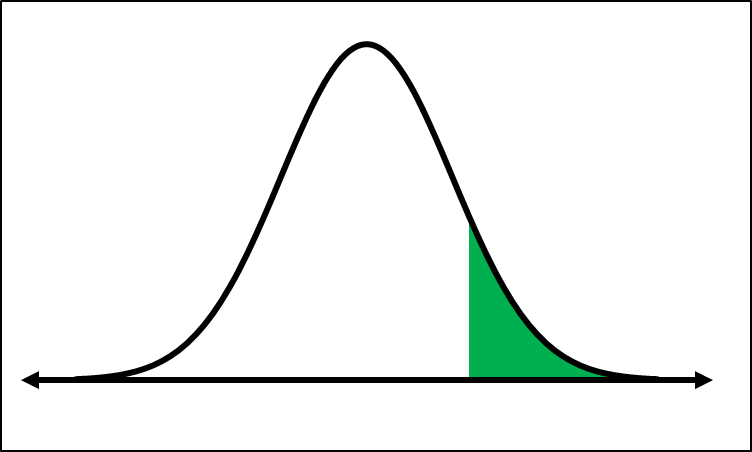
When using a calculator, the first step is to visualize the problem by sketching a graph. For instance, if you want to find the probability that a z-score is less than -0.81, you would draw a normal distribution curve, marking the z-score on the x-axis. The area to the left of this z-score represents the probability.

To calculate this using the TI-84, access the distribution menu by pressing 2nd followed by VARS. From there, select the normalcdf function for numerical output or shade normal for a graphical representation. For a probability that z is less than a specific value, set the lower bound to a very large negative number (e.g., -1E99) and the upper bound to the z-score in question, which in this case is -0.81. The mean (μ) is 0 and the standard deviation (σ) is 1 for a standard normal distribution, so these values remain unchanged. After entering these parameters, hitting the DRAW button will display the graph and the corresponding area, which represents the probability.

For example, the area calculated for z < -0.81 is approximately 0.209, matching the value obtained from the z-table.

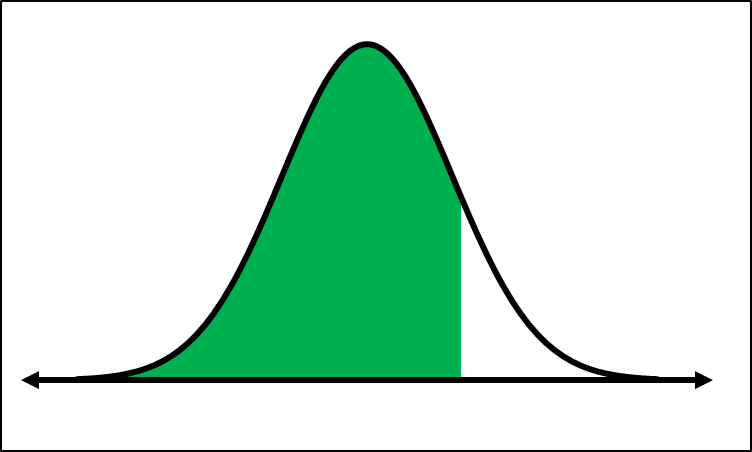
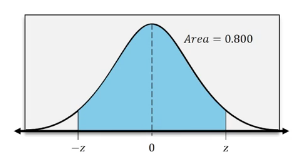
In scenarios where you need to find the probability between two z-scores, such as between -1 and 1, the process is similar. Again, sketch the normal distribution curve, marking both z-scores. This time, when using the calculator, set the lower bound to -1 and the upper bound to 1. The calculator will then compute the area between these two z-scores, which represents the probability of a z-score falling within that range. For this example, the area calculated is approximately 0.6827, confirming the results from previous calculations.

Utilizing a graphing calculator not only streamlines the process of finding probabilities associated with z-scores but also reduces the likelihood of errors that can occur when using a z-table. This method is particularly beneficial for more complex problems involving multiple z-scores or when visual representation aids in understanding the distribution of data.

In statistics, understanding how to find a z-score from a given probability is essential, especially when working with the normal distribution. The z-score represents the number of standard deviations a data point is from the mean. When given a probability, you can use the inverse normal function on a TI-84 calculator to find the corresponding z-score.

To illustrate this process, consider a scenario where you have a probability that z is less than an unknown z-score, specifically \( P(Z < z) = 0.0853 \). This probability indicates a small area under the normal curve, suggesting that the z-score will be negative. To find the z-score, start by sketching a normal distribution graph, marking the area to the left of the unknown z-score. This visual representation helps in understanding the problem context.

Next, access the inverse normal function on your calculator by pressing the 2nd button followed by VARS, and select the invNorm option. Input the probability (0.0853), and for a standard normal distribution, set the mean (\( \mu \)) to 0 and the standard deviation (\( \sigma \)) to 1. Since the area is to the left, select the left tail option. After hitting Paste and then Enter, the calculator will output the z-score, which in this case is approximately -1.37. This aligns with the expectation of a negative value based on the graph.

In another example, suppose you need to find a z-score where the probability that z is greater than some unknown number is given as \( P(Z > z) = 0.3409 \). This indicates an area to the right of the z-score. Again, sketch the normal distribution, noting that this area is larger than the previous example, suggesting a positive z-score. Follow the same steps on the calculator: access the inverse normal function, input the probability (0.3409), and set \( \mu = 0 \) and \( \sigma = 1 \). However, since this probability represents the right tail, you must select the right tail option. The calculator will then provide a z-score of approximately 0.41, which is consistent with the expectation of a small positive number.

For users of the standard TI-84 (not the CE version), it’s important to note that the calculator defaults to assuming left tail probabilities. Therefore, when given a right tail probability, you must convert it by calculating \( 1 - P(Z > z) \) to find the corresponding left tail probability. In this case, you would compute \( 1 - 0.3409 = 0.6591 \) and input that into the calculator to find the z-score.

Understanding these steps and the functionality of the inverse normal function is crucial for accurately determining z-scores from probabilities, enhancing your statistical analysis skills.