Mean: Videos & Practice Problems

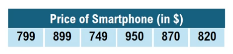
Understanding how to calculate the mean is essential for interpreting data numerically. The mean, often referred to as the average, is a measure of central tendency that summarizes a dataset with a single value. To find the mean, you add all the values in a dataset and then divide by the total number of values.

For example, consider the dataset consisting of the numbers 5, 10, 12, 14, and 3. To calculate the mean, you first sum these values:

5 + 10 + 12 + 14 + 3 = 44

Next, divide this sum by the number of values, which in this case is 5:

Mean = \(\frac{44}{5} = 8.8\)

This result indicates that the mean of this dataset is 8.8, providing a central value around which the other numbers are distributed.

In mathematical notation, the mean is often represented as \(\bar{x}\), where the formula is expressed as:

\(\bar{x} = \frac{\Sigma x}{n}\)

Here, \(\Sigma\) (the Greek capital letter sigma) signifies the sum of all values in the dataset, \(x\) represents each individual value, and \(n\) is the total number of values. This formula encapsulates the process of calculating the mean succinctly.

When dealing with a larger population, the mean is calculated in the same manner, but different symbols may be used. For instance, the population mean is denoted by the Greek letter \(\mu\) and is calculated using:

\(\mu = \frac{\Sigma X}{N}\)

In this case, \(N\) represents the total number of values in the population. Despite the different symbols, the underlying calculation remains consistent.

It is important to note that the mean can be significantly affected by outliers—extreme values that differ greatly from other observations. For instance, if we add the number 76 to our previous dataset, the new sum becomes:

5 + 10 + 12 + 14 + 3 + 76 = 120

Now, dividing by the new total of 6 values gives:

Mean = \(\frac{120}{6} = 20\)

This demonstrates how the inclusion of an outlier can shift the mean from 8.8 to 20, illustrating the sensitivity of the mean to extreme values.

In summary, the mean serves as a valuable statistical tool for summarizing data, but it is crucial to be aware of how outliers can influence its value. Understanding these concepts will enhance your ability to analyze and interpret data effectively.

In analyzing heart rates from a sample of adult males and females, we aim to determine if there is a significant difference in their mean heart rates. To do this, we first calculate the sample means for both groups using the formula for the mean:

Mean (x̄) = \(\frac{\sum x}{n}\)

where \(\sum x\) is the sum of all values and \(n\) is the total number of observations. In this case, both samples consist of 10 individuals.

For the male sample, we sum the heart rates: 84, 70, 68, 59, 61, 77, 90, 65, 56, and 72. The calculation proceeds as follows:

x̄ (males) = \(\frac{84 + 70 + 68 + 59 + 61 + 77 + 90 + 65 + 56 + 72}{10} = \frac{ 84 + 70 + 68 + 59 + 61 + 77 + 90 + 65 + 56 + 72}{10} = 70.2\)

Next, we calculate the mean for the female sample using the heart rates: 80, 73, 88, 91, 69, 85, 91, 81, 79, and 77. The calculation is as follows:

x̄ (females) = \(\frac{80 + 73 + 88 + 91 + 69 + 85 + 91 + 81 + 79 + 77}{10} = \frac{ 80 + 73 + 88 + 91 + 69 + 85 + 91 + 81 + 79 + 77}{10} = 81.4\)

After calculating the means, we find that the mean heart rate for females (81.4 bpm) is higher than that for males (70.2 bpm). This difference suggests a biological variance in heart rates between genders. Therefore, we conclude that there is a significant difference in mean heart rates, expressed as:

x̄ (females) > x̄ (males)

This analysis highlights the importance of statistical calculations in interpreting biological data, allowing us to draw meaningful conclusions from the observed differences in heart rates.