A school administrator wants to examine whether students' academic performance differs based on the type of instructional method used in their classes. A random sample of 18 18 18 students is selected and divided evenly among the three teaching methods. After a semester, all students take the same standardized final exam. State the null and alternative hypotheses for a one-way ANOVA test.

H 0 H_0 H 0 : All students perform equally well on the final exam, regardless of the instructional method. H 1 H_1 H 1 : At least one group of students performs differently than the others.

H 0 H_0 H 0 : The three instructional methods lead to different mean exam scores. H 1 H_1 H 1 : All three instructional methods lead to the same mean exam scores.

H 0 H_0 H 0 : There is a significant difference among the teaching methods. H 1 H_1 H 1 : There is no significant difference among the teaching methods.

14. ANOVA

Introduction to ANOVA

14. ANOVA

Introduction to ANOVA: Videos & Practice Problems

Video Lessons Worksheet

Topic summary

concept

Introduction to ANOVA

Video duration:

Problem

A company wants to determine whether the average monthly sales differ among three different regions: North, South, and West. The company collects monthly sales data (in thousands of dollars) from four randomly selected stores in each region over the same month. Calculate the F-statistic given the Mean Square due to Treatments: MST = $226.6$ (variance between groups) and the Mean Square due to Error: MSE = $7.944$ (variance within groups).

$7.94$

$28.52$

$226.6$

$0.035$

Problem

Four different high schools in local towns took random samples of 100 students in three grades, $10^{\operatorname{th}}-12^{\operatorname{th}}$ and collected data on the weekly time spent studying to see if students in each of these grades study on average for the same amount of time per week. The four schools ran ANOVA tests on their samples, and the F-Statistics were $2.35$ , $2.57$ , $2.81$ , and $3.93$ . Which F-Statistic is most likely to indicate the average study times across grades are not all the same?

$2.35$

$2.57$

$2.81$

$3.93$

concept

ANOVA Test

Video duration:

Problem

A school administrator wants to examine whether students' academic performance differs based on the type of instructional method used in their classes. A random sample of $18$ students is selected and divided evenly among the three teaching methods. After a semester, all students take the same standardized final exam. State the null and alternative hypotheses for a one-way ANOVA test.

$H_0$ : All means are the same

$H_{A}$ : At least one mean is different, at least one method has a different average test score.

$H_0$ : All students perform equally well on the final exam, regardless of the instructional method.

$H_1$ : At least one group of students performs differently than the others.

$H_0$ : The three instructional methods lead to different mean exam scores.

$H_1$ : All three instructional methods lead to the same mean exam scores.

$H_0$ : There is a significant difference among the teaching methods.

$H_1$ : There is no significant difference among the teaching methods.

Problem

A school administrator wants to examine whether students' academic performance differs based on the type of instructional method used in their classes. A random sample of $18$ students is selected and divided evenly among the three teaching methods. After a semester, all students take the same standardized final exam. An ANOVA test is performed and results in a P-value of $1.403\bullet10^{-7}$ . Interpret these results.

The P-value is very high, so there is insufficient evidence to suggest that the type of instructional method has an effect on academic performance.

At least one method has a different average test score. Reject the null hypothesis.

There is no difference in academic performance, but further testing is required to make a definitive conclusion.

The P-value is close to 1, suggesting that the type of instructional method has no impact on students' academic performance.

Problem

A marketing manager wants to evaluate whether three different advertising platforms-TV, social media, and print media-lead to different average sales performance across regional stores. She runs a 4-week advertising campaign, assigning one platform to a group of 5 stores each (15 stores total). After the campaign, she collects the average weekly sales (in $1,000s) for each store during the campaign period. She wants to determine whether there is a statistically significant difference in mean sales among the three advertising platforms. State the null & alternative hypotheses for a one-way ANOVA test.

$H sub 0$ : All means are the same

$H_{a}$ : At least one advertising platform leads to a significant difference in average sales.

$H_0$ : At least one advertising platform leads to a significant difference in average sales.

$H_{a}$ : All means are the same.

$H_0$ : There is a significant difference in the mean sales among the three advertising platforms.

$H_{a}$ : There is no significant difference in the mean sales among the three advertising platforms.

$H_0$ : The mean sales are equal for TV advertising but differ for social media and print media platforms.

$H_{a}$ : The mean sales differ for all three advertising platforms.

Problem

A marketing manager wants to evaluate whether three different advertising platforms-TV, social media, and print media-lead to different average sales performance across regional stores. She runs a 4-wook advertising campaign, assigning one platform to a group of 5 stores each (15 stores total). After the campaign, she collects the weekly soles (in $1,000s) for each store during the campaign period. She wants to determine whether there is a statistically significant difference in mean sales among the three advertising platforms. In an ANOVA test a P-value of 0.03 is obtained. What can be concluded about mean weekly sales for different advertising platforms?

Since the P-value (0.03) is greater than the significance level (typically 0.05), we fail to reject the null hypothesis and conclude that there is no significant difference in mean sales among the platforms. $0.03$

Since the P-value (0.03) is greater than 0.05, we reject the null hypothesis and conclude that there is a significant difference in the mean sales across the platforms.

Since the P-value (0.03) is less than 0.05, we fail to reject the null hypothesis and conclude that there is no significant difference in mean sales across the platforms.

Since the P-value (0.03) is less than the significance level (typically 0.05), at least one advertising platforms leads to a significant difference in average sales.

concept

ANOVA Test Using TI-84

Video duration:

Problem

A regional sales director wants to determine whether different customer service training programs lead to different levels of employee performance across three branches. Each branch uses one of the following training programs: Program A. Program B, or Program C. After one month, the director measures the performance score (out of 100) for 5 randomly selected employees from each branch. Using $\alpha=0.05$ , perform a one-way ANOVA to determine whether there is a statistically significant difference in mean performance among the three training programs.

Since the performance scores for all three programs (A, B, and C) range from 76 to 85, there is no statistically significant difference between the training programs.

The P-value from the one-way ANOVA is greater than 0.05, so we fail to reject the null hypothesis and conclude that the type of training program does not affect employee performance.

The P-value from the one-way ANOVA is less than 0.05, so we reject the $H sub 0$ and suggest $H_{α}$ .

The one-way ANOVA is inappropriate for this study because it compares two groups only, a different statistical test should be used.

example

ANOVA Test Using TI-84 Example 1

Video duration:

ANOVA Test Using TI-84 Example 1 Video Summary

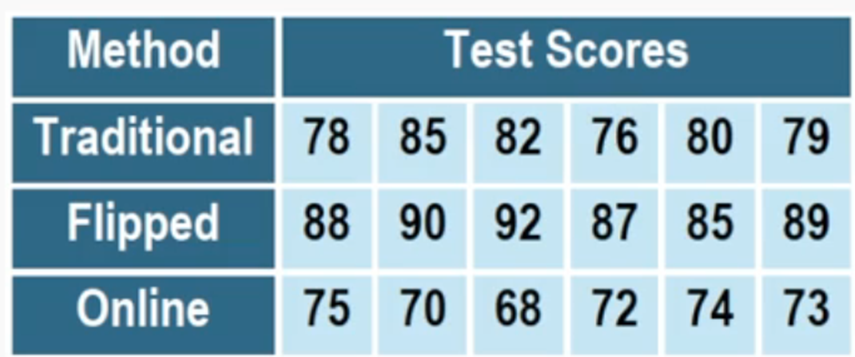
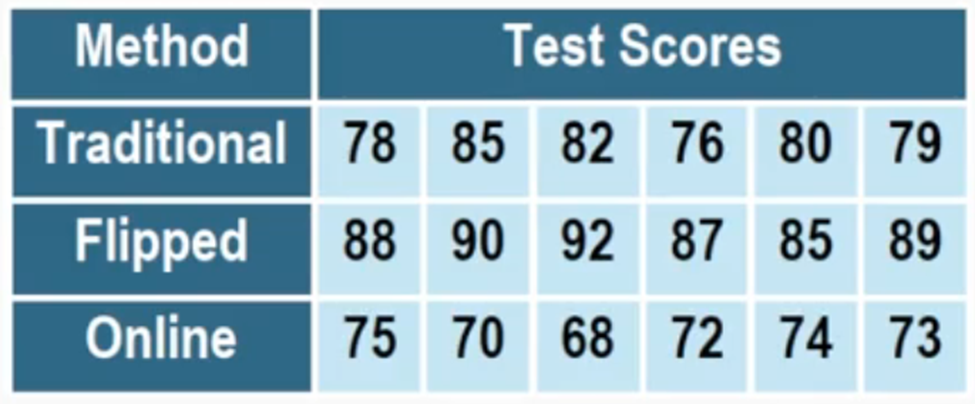
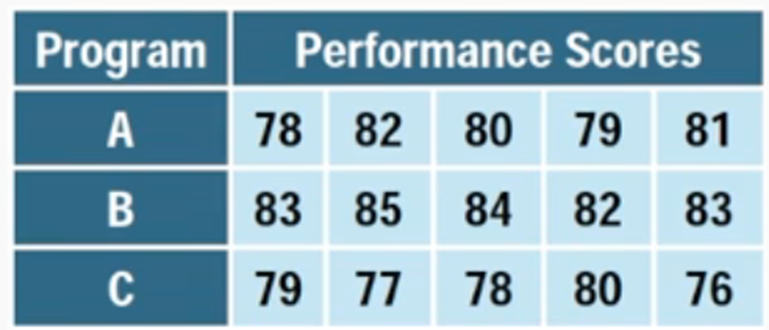
In this scenario, a nutritionist is investigating the effectiveness of three different diet plans (A, B, and C) by conducting an experiment over six weeks with 15 participants, assigning five individuals to each diet plan. The primary goal is to determine if there is a significant difference in mean weight loss among the three diets. To analyze the data, an Analysis of Variance (ANOVA) test is employed, which is suitable for comparing the means of multiple groups.

The first step in the analysis involves formulating the null and alternative hypotheses. The null hypothesis states that the mean weight loss for all three diet plans is equal, expressed mathematically as:

\[ H_0: \mu_A = \mu_B = \mu_C \]

Conversely, the alternative hypothesis posits that at least one diet plan has a different mean weight loss, represented as:

\[ H_a: \text{At least one } \mu \text{ is different} \]

To perform the ANOVA test using a TI-84 calculator, the data for each diet plan is entered into separate lists. After entering the data, the user navigates to the statistical tests menu, selects the ANOVA test option, and inputs the corresponding lists for the three diet plans.

Upon running the test, the calculator provides an F-statistic of 25.298 and a p-value of approximately $4.96 \times 10^{-4}$. This p-value is significantly lower than the common alpha level of 0.05, leading to the rejection of the null hypothesis. Therefore, it can be concluded that at least one of the diet plans results in a significantly different amount of weight loss.

This analysis highlights the importance of using ANOVA for comparing means across multiple groups and demonstrates how statistical tools can aid in making informed decisions based on experimental data.

Your Statistics for Business tutors

Patrick Ford

Physics and Math Lead Instructor

Colleen Daly