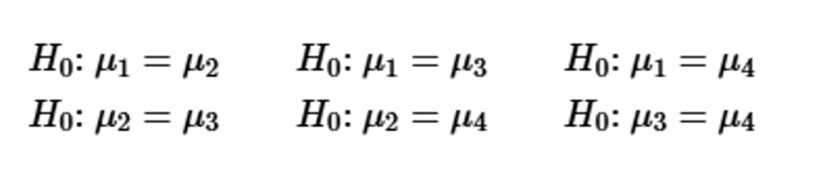Back
BackProblem 12.c.1d
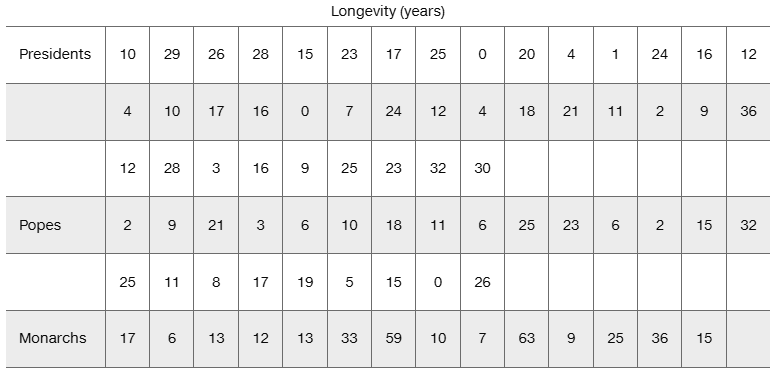
In Exercises 1–5, refer to the following list of numbers of years that deceased U.S. presidents, popes, and British monarchs lived after their inauguration, election, or coronation, respectively. (As of this writing, the last president is George H. W. Bush, the last pope is John Paul II, and the last British monarch is George VI.) Assume that the data are samples from larger populations.
[Image]
Exploring the Data Include appropriate units in all answers.
d. Are there any obvious outliers?
Problem 12.CRE.8
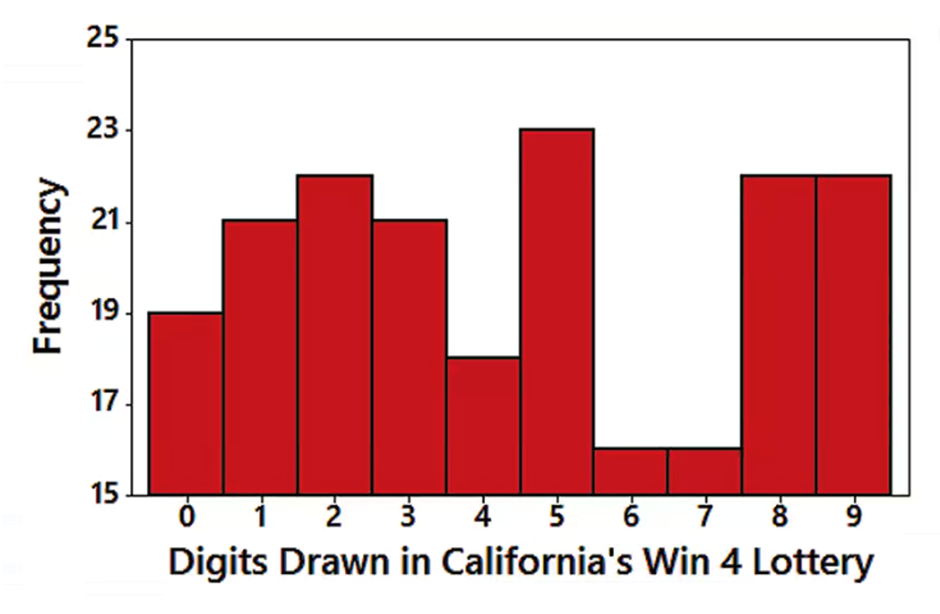
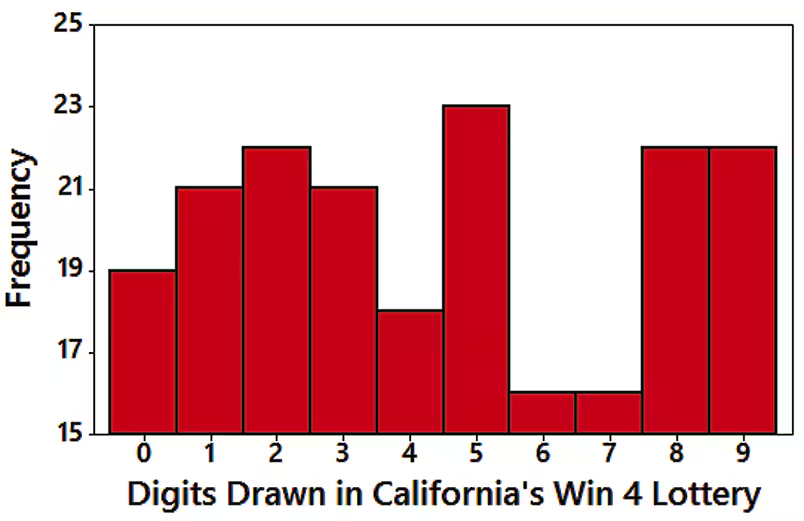
Win 4 Lottery Shown below is a histogram of digits selected in California’s Win 4 lottery. Each drawing involves the random selection (with replacement) of four digits between 0 and 9 inclusive.
b. Does the display depict a normal distribution? Why or why not? What should be the shape of the histogram?
Problem 12.CRE.1e
In Exercises 1–5, refer to the following list of numbers of years that deceased U.S. presidents, popes, and British monarchs lived after their inauguration, election, or coronation, respectively. (As of this writing, the last president is George H. W. Bush, the last pope is John Paul II, and the last British monarch is George VI.) Assume that the data are samples from larger populations.
[Image]
Exploring the Data Include appropriate units in all answers.
e. What is the level of measurement of the data (nominal, ordinal, interval, ratio)?
Problem 12.CRE.8c
Win 4 Lottery Shown below is a histogram of digits selected in California’s Win 4 lottery. Each drawing involves the random selection (with replacement) of four digits between 0 and 9 inclusive.
c. Identify the frequencies, then test the claim that the digits are selected from a population in which the digits are all equally likely. Is there a problem with the lottery?
Problem 12.CR.6b
Quarters Assume that weights of quarters minted after 1964 are normally distributed with a mean of 5.670 g and a standard deviation of 0.062 g (based on U.S. Mint specifications).
b. If 25 quarters are randomly selected, find the probability that their mean weight is greater than 5.675 g.
Problem 12.CR.3
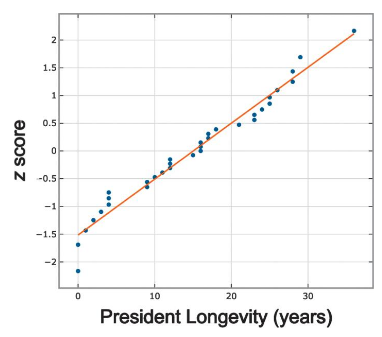
Normal Quantile Plot The accompanying normal quantile plot was obtained from the longevity times of presidents. What does this graph tell us?
Problem 12.CQ.1
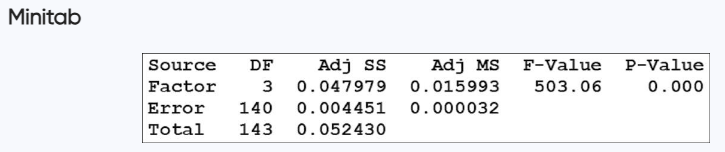
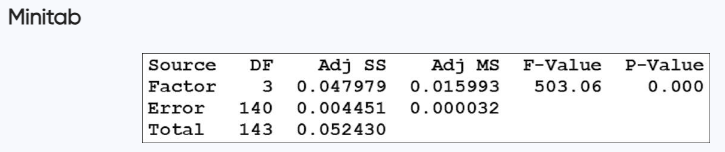
Cola Weights Data Set 37 “Cola Weights and Volumes” in Appendix B lists the weights (lb) of the contents of cans of cola from four different samples: (1) regular Coke, (2) Diet Coke, (3) regular Pepsi, and (4) Diet Pepsi. The results from analysis of variance are shown in the Minitab display below. What is the null hypothesis for this analysis of variance test? Based on the displayed results, what should you conclude about H_knot. What do you conclude about equality of the mean weights from the four samples?
Problem 12.CQ.2
Cola Weights For the four samples described in Exercise 1, the sample of regular Coke has a mean weight of 0.81682 lb, the sample of Diet Coke has a mean weight of 0.78479 lb, the sample of regular Pepsi has a mean weight of 0.82410 lb, and the sample of Diet Pepsi has a mean weight of 0.78386 lb. If we use analysis of variance and reach a conclusion to reject equality of the four sample means, can we then conclude that any of the specific samples have means that are significantly different from the others?
Problem 12.CQ.5
Cola Weights The displayed results from Exercise 1 are from one-way analysis of variance. What is it about this test that characterizes it as one-way analysis of variance instead of two-way analysis of variance?
Problem 12.R.4
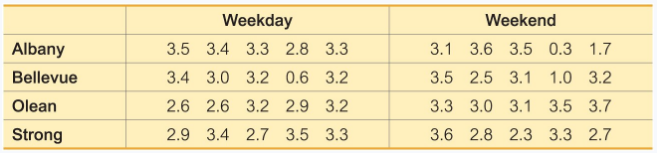
Birth Weights The table below lists some of the same data used in the preceding exercise, but the seven days of the week are combined into weekday (Monday, Tuesday, Wednesday, Thursday, Friday) and weekend days (Saturday, Sunday). Also, the birth weights are converted to kilograms. What do you conclude?
Problem 12.1.3a
Interaction
a. What is an interaction between two factors?
Problem 12.1.3b
Interaction
b. In general, when using two-way analysis of variance, if we find that there is an interaction effect, how does that affect the procedure?
Problem 12.1.9
In Exercises 5–16, use analysis of variance for the indicated test.
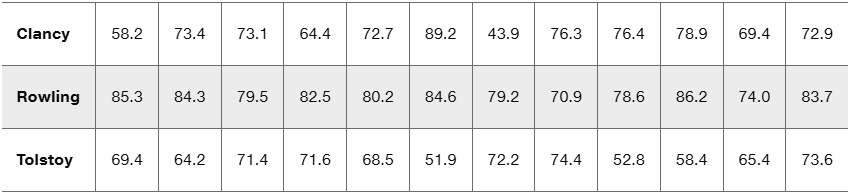
Clancy, Rowling, and Tolstoy Ease of Reading Pages were randomly selected from three books: The Bear and the Dragon by Tom Clancy, Harry Potter and the Sorcerer’s Stone by J.K. Rowling, and War and Peace by Leo Tolstoy. Listed below are Flesch Reading Ease Scores for those pages. Use a 0.05 significance level to test the claim that pages from books by those three authors have the same mean Flesch Reading Ease score. Given that higher scores correspond to text that is easier to read, which author appears to be different, and how is that author different?
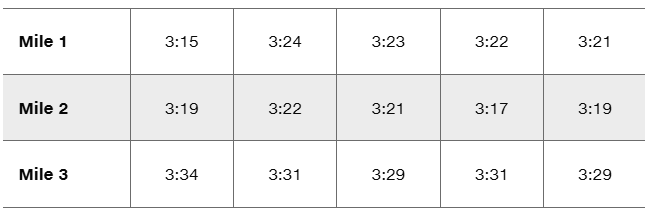
Problem 12.1.11
In Exercises 5–16, use analysis of variance for the indicated test.
Triathlon Times Jeff Parent is a statistics instructor who participates in triathlons. Listed below are times (in minutes and seconds) he recorded while riding a bicycle for five stages through each mile of a 3-mile loop. Use a 0.05 significance level to test the claim that it takes the same time to ride each of the miles. Does one of the miles appear to have a hill?
Problem 12.1.2
Two-Way Anova If we have a goal of using the data given in Exercise 1 to (1) determine whether the femur side (left, right) has an effect on the crash force measurements and (2) to determine whether the vehicle size has an effect on the crash force measurements, should we use one-way analysis of variance for the two individual tests? Why or why not?
Problem 12.1.1a
In Exercises 1–4, use the following listed measured amounts of chest compression (mm) from car crash tests (from Data Set 35 “Car Data” in Appendix B). Also shown are the SPSS results from analysis of variance. Assume that we plan to use a 0.05 significance level to test the claim that the different car sizes have the same mean amount of chest compression.
Anova
a. What characteristic of the data above indicates that we should use one-way analysis of variance?
Problem 12.1.1b
In Exercises 1–4, use the following listed measured amounts of chest compression (mm) from car crash tests (from Data Set 35 “Car Data” in Appendix B). Also shown are the SPSS results from analysis of variance. Assume that we plan to use a 0.05 significance level to test the claim that the different car sizes have the same mean amount of chest compression.
Anova
b. If the objective is to test the claim that the four car sizes have the same mean chest compression, why is the method referred to as analysis of variance?
Problem 12.1.2
In Exercises 1–4, use the following listed measured amounts of chest compression (mm) from car crash tests (from Data Set 35 “Car Data” in Appendix B). Also shown are the SPSS results from analysis of variance. Assume that we plan to use a 0.05 significance level to test the claim that the different car sizes have the same mean amount of chest compression.
Why Not Test Two at a Time? Refer to the sample data given in Exercise 1. If we want to test for equality of the four means, why don’t we use the methods of Section 9-2 “Two Means: Independent Samples” for the following six separate hypothesis tests?
Problem 12.2.11a
Transformations of Data Example 1 illustrated the use of two-way ANOVA to analyze the sample data in Table 12-3. How are the results affected in each of the following cases?
a. The same constant is added to each sample value.
Problem 12.2.11b
Transformations of Data Example 1 illustrated the use of two-way ANOVA to analyze the sample data in Table 12-3. How are the results affected in each of the following cases?
b. Each sample value is multiplied by the same nonzero constant.
Problem 12.2.11c
Transformations of Data Example 1 illustrated the use of two-way ANOVA to analyze the sample data in Table 12-3. How are the results affected in each of the following cases?
c. The format of the table is transposed so that the row and column factors are interchanged.
Problem 12.2.11d
Transformations of Data Example 1 illustrated the use of two-way ANOVA to analyze the sample data in Table 12-3. How are the results affected in each of the following cases?
d. The first sample value in the first cell is changed so that it becomes an outlier.
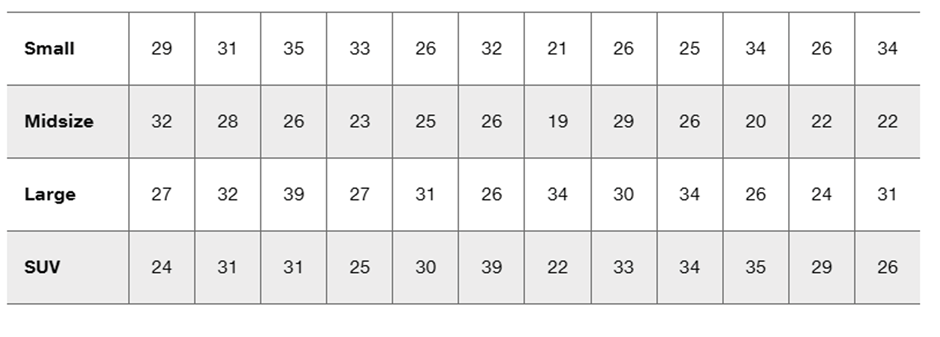
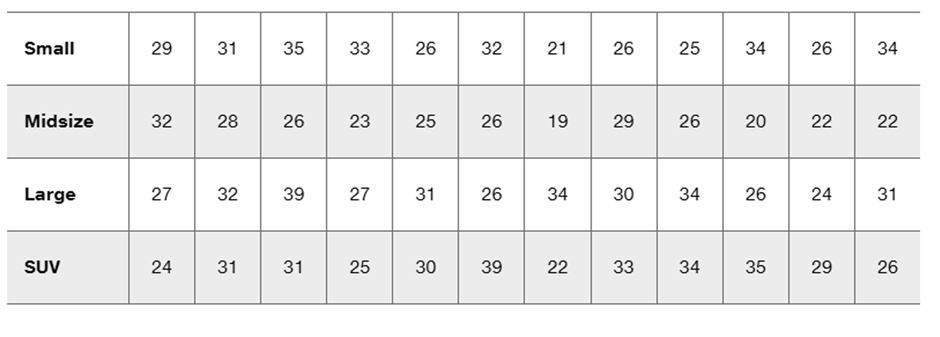
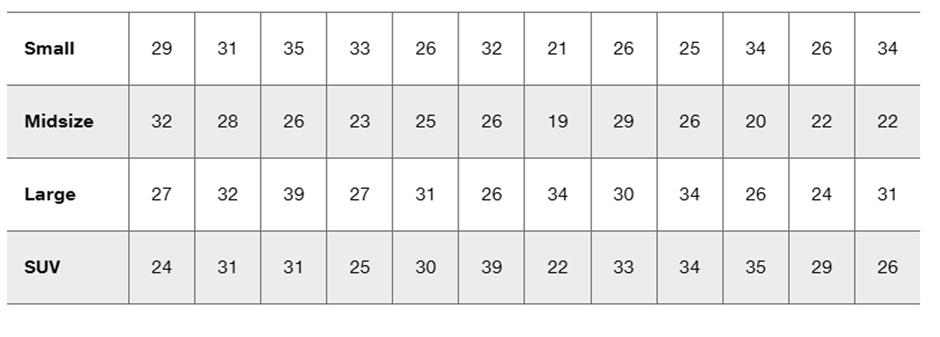
Problem 12.2.1
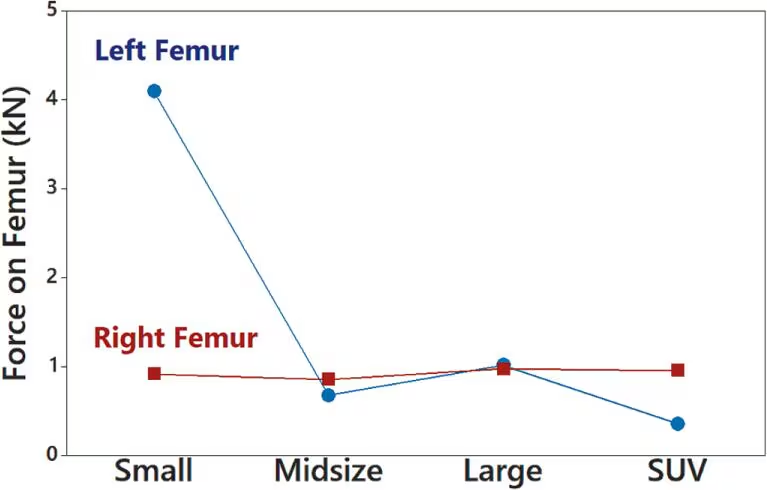
Two-Way Anova The measurements of crash test forces on the femur in Table 12-3 from Example 1 are reproduced below with fabricated measurement data (in red) used for the left femur in a small car. What characteristic of the data suggests that the appropriate method of analysis is two-way analysis of variance? That is, what is “two-way” about the data entered in this table?
Problem 12.2.3c
c. Shown below is an interaction graph constructed from the data in Exercise 1. What does the graph suggest?
Problem 12.2.4
Balanced Design Does the table given in Exercise 1 constitute a balanced design? Why or why not?
Problem 12.2.5
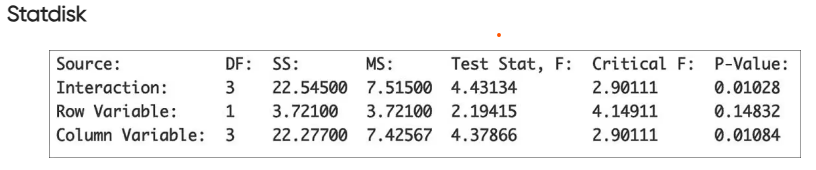
Car Crash Test Measurements If we use the data given in Exercise 1 with two-way analysis of variance and a 0.05 significance level, we get the accompanying display. What do you conclude?
Problem 12.2.7
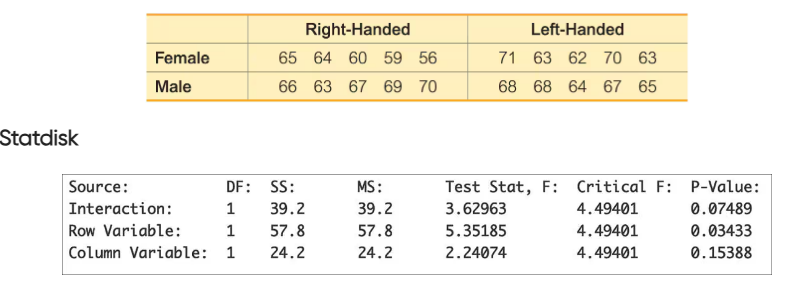
Distance Between Pupils The following table lists distances (mm) between pupils of randomly selected U.S. Army personnel collected as part of the ANSUR II study. Results from two-way analysis of variance are also shown. Use the displayed results and use a 0.05 significance level. What do you conclude? Are the results as you would expect?
Problem 12.2.9
Sitting Heights The sitting height of a person is the vertical distance between the sitting surface and the top of the head. The following table lists sitting heights (mm) of randomly selected U.S. Army personnel collected as part of the ANSUR II study. Using the data with a 0.05 significance level, what do you conclude? Are the results as you would expect?
Problem 12.6
One-Way ANOVA In general, what is one-way analysis of variance used for?