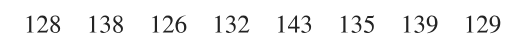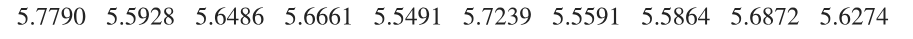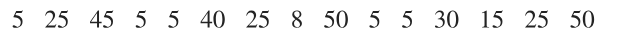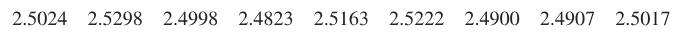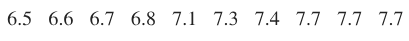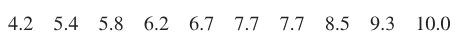Archeology Archeologists have studied sizes of Egyptian skulls in an attempt to determine whether breeding occurred between different cultures. Listed below are the widths (mm) of skulls from 150 A.D. (based on data from Ancient Races of the Thebaid by Thomson and Randall-Maciver). Construct a 99% confidence interval estimate of the mean skull width.

Minting Quarters Listed below are weights (grams) of quarters minted after 1964 (based on Data Set 40 “Coin Weights” in Appendix B). Construct a 95% confidence interval estimate of the mean weight of all quarters minted after 1964. Specifications require that the quarters have a weight of 5.670 g. What does the confidence interval suggest about that specification?

Los Angeles Commute Time Listed below are 15 Los Angeles commute times (based on a sample from Data Set 31 “Commute Times” in Appendix B). Construct a 99% confidence interval estimate of the population mean. Is the confidence interval a good estimate of the population mean?

Genes Samples of DNA are collected, and the four DNA bases of A, G, C, and T are coded as 1, 2, 3, and 4, respectively. The results are listed below. Construct a 95% confidence interval estimate of the mean. What is the practical use of the confidence interval?

2 2 1 4 3 3 3 3 4 1

Mercury in Sushi An FDA guideline is that the mercury in fish should be below 1 part per million (ppm). Listed below are the amounts of mercury (ppm) found in tuna sushi sampled at different stores in New York City. The study was sponsored by the New York Times, and the stores (in order) are D’Agostino, Eli’s Manhattan, Fairway, Food Emporium, Gourmet Garage, Grace’s Marketplace, and Whole Foods. Construct a 98% confidence interval estimate of the mean amount of mercury in the population. Does it appear that there is too much mercury in tuna sushi?

0.56 0.75 0.10 0.95 1.25 0.54 0.88

Mean IQ of Data Scientists See the preceding exercise, in which we can assume that sigma=15 for the IQ scores. Data scientists are a group with IQ scores that vary less than the IQ scores of the general population. Find the sample size needed to estimate the mean IQ of data scientists, given that we want 98% confidence that the sample mean is within 2 IQ points of the population mean. Does the sample size appear to be practical?

Ages of Moviegoers Find the sample size needed to estimate the mean age of movie patrons, given that we want 98% confidence that the sample mean is within 1.5 years of the population mean. Assume that sigma=19.6 years, based on a previous report from the Motion Picture Association of America. Could the sample be obtained from one movie at one theater?

Mean Pulse Rate of Males Data Set 1 “Body Data” in Appendix B includes pulse rates of 153 randomly selected adult males, and those pulse rates vary from a low of 40 bpm to a high of 104 bpm. Find the minimum sample size required to estimate the mean pulse rate of adult males. Assume that we want 99% confidence that the sample mean is within 2 bpm of the population mean.

a. Find the sample size using the range rule of thumb to estimate .

Mean Pulse Rate of Males Data Set 1 “Body Data” in Appendix B includes pulse rates of 153 randomly selected adult males, and those pulse rates vary from a low of 40 bpm to a high of 104 bpm. Find the minimum sample size required to estimate the mean pulse rate of adult males. Assume that we want 99% confidence that the sample mean is within 2 bpm of the population mean.

b. Assume that sigma=11.3 bpm, based on the value of s=11.3 bpm for the sample of 153 male pulse rates.

Mean Pulse Rate of Females Data Set 1 “Body Data” in Appendix B includes pulse rates of 147 randomly selected adult females, and those pulse rates vary from a low of 36 bpm to a high of 104 bpm. Find the minimum sample size required to estimate the mean pulse rate of adult females. Assume that we want 99% confidence that the sample mean is within 2 bpm of the population mean.

b. Assume that sigma=12.5 bpm, based on the value of s=12.5 bpm for the sample of 147 female pulse rates.

Mean Body Temperature Data Set 5 “Body Temperatures” in Appendix B includes 106 body temperatures of adults for Day 2 at 12 AM, and they vary from a low of 96.5F to a high of 99.6F. Find the minimum sample size required to estimate the mean body temperature of all adults. Assume that we want 98% confidence that the sample mean is within 0.1F of the population mean.

b. Assume that sigma=0.62F, based on the value of s=0.62F for the sample of 106 body temperatures.

Second-Hand Smoke Refer to Data Set 15 “Passive and Active Smoke” and construct a 95% confidence interval estimates of the mean cotinine level in each of three samples: (1) people who smoke; (2) people who don’t smoke but are exposed to tobacco smoke at home or work; (3) people who don’t smoke and are not exposed to smoke. Measuring cotinine in people’s blood is the most reliable way to determine exposure to nicotine. What do the confidence intervals suggest about the effects of smoking and second-hand smoke?

Large Data Sets from Appendix B. In Exercises 21 and 22, use the data set in Appendix B. Assume that each sample is a simple random sample obtained from a population with a normal distribution.

Comparing Waiting Lines Refer to Data Set 30 “Queues” in Appendix B. Construct separate 95% confidence interval estimates of using the two-line wait times and the single-line wait times. Do the results support the expectation that the single line has less variation? Do the wait times from both line configurations satisfy the requirements for confidence interval estimates of sigma

Determining Sample Size. Assume that each sample is a simple random sample obtained from a normally distributed population.

You want to estimate for the population of diastolic blood pressures of air traffic controllers in the United States. Find the minimum sample size needed to be 95% confident that the sample standard deviation s is within 1% of σ. Is this sample size practical?

Red Blood Cell Count Here is a 95% confidence interval estimate of obtained by using the red blood cell counts of adult females listed in Data Set 1 “Body Data” in Appendix B:

[Image].

Identify the corresponding confidence interval estimate of and include the appropriate units.

Use the given information to find the number of degrees of freedom, the critical values X2L and X2R, and the confidence interval estimate of σ. It is reasonable to assume that a simple random sample has been selected from a population with a normal distribution:

Nicotine in Menthol Cigarettes 95% confidence; n = 25, s = 0.24 mg

use the given information to find the number of degrees of freedom, the critical values X2L and X2R, and the confidence interval estimate of σ. It is reasonable to assume that a simple random sample has been selected from a population with a normal distribution:

Heights of Men 99% confidence; n=153, s=7.10 cm.

Body Temperature Data Set 5 “Body Temperatures” in Appendix B includes a sample of 106 body temperatures having a mean of and a standard deviation of 0.62F (for day 2 at 12 AM). Construct a 95% confidence interval estimate of the standard deviation of the body temperatures for the entire population.

Atkins Weight Loss Program In a test of weight loss programs, 40 adults used the Atkins weight loss program. After 12 months, their mean weight loss was found to be 2.1 lb, with a standard deviation of 4.8 lb. Construct a 90% confidence interval estimate of the standard deviation of the weight loss for all such subjects. Does the confidence interval give us information about the effectiveness of the diet?

Large Data Sets from Appendix B. In Exercises 21 and 22, use the data set in Appendix B. Assume that each sample is a simple random sample obtained from a population with a normal distribution.

Birth Weights Refer to Data Set 6 “Births” in Appendix B.

a. Use the 205 birth weights of girls to construct a 95% confidence interval estimate of the standard deviation of the population from which the sample was obtained.

FINDING SAMPLE SIZE Instead of using Table 7-2 for determining the sample size required to estimate a population standard deviation σ, the following formula can also be used

$n=\frac{1}{2}{\left(\frac{z_{\alpha /2}}{d}\right)}^2$

where $z_{{}_{}\alpha /2}$ corresponds to the confidence level and d is the decimal form of the percentage error. For example, to be 95% confident that s is within 15% of the value of σ, use zα/2=1.96 and d=0.15 to get a sample size of n=86. Find the sample size required to estimate the standard deviation of IQ scores of data scientists, assuming that we want 98% confidence that s is within 5% of σ.

Mint Specs Listed below are weights (grams) from a simple random sample of pennies produced after 1983 (from Data Set 40 “Coin Weights” in Appendix B). Construct a 95% confidence interval estimate of for the population of such pennies. What does the confidence interval suggest about the U.S. Mint specifications that now require a standard deviation of 0.0230 g for weights of pennies?

Professor Evaluation Scores Listed below are student evaluation scores of professors from Data Set 28 “Course Evaluations” in Appendix B. Construct a 95% confidence interval estimate of for each of the two data sets. Does there appear to be a difference in variation?

Comparing Waiting Lines

The values listed below are waiting times (in minutes) of customers at the Jefferson Valley Bank, where customers enter a single waiting line that feeds three teller windows. Construct a 95% confidence interval for the population standard deviation sigma.

Comparing Waiting Lines

The values listed below are waiting times (in minutes) of customers at the Bank of Providence, where customers may enter any one of three different lines that have formed at three teller windows. Construct a 95% confidence interval for the population standard deviation sigma.

Voting Survey In a survey of 1002 people, 70% said that they voted in a recent presidential election (based on data from ICR Research Group). Voting records show that 61% of eligible voters actually did vote.

a. Among the 1002 people surveyed, what is the actual number of people who said that they voted?

Voting Survey In a survey of 1002 people, 70% said that they voted in a recent presidential election (based on data from ICR Research Group). Voting records show that 61% of eligible voters actually did vote.

b. Find a 95% confidence interval estimate of the percentage of people who say that they voted.

Voting Survey In a survey of 1002 people, 70% said that they voted in a recent presidential election (based on data from ICR Research Group). Voting records show that 61% of eligible voters actually did vote.

d. Are the survey results consistent with the actual voter turnout of 61%? Why or why not?

Mean Assume that we want to use the sample data given in Exercise 1 with the bootstrap method to estimate the population mean. The mean of the values in Exercise 1 is 54.3 seconds, and the mean of all of the tobacco times in Data Set 20 “Alcohol and Tobacco in Movies” from Appendix B is 57.4 seconds. If we use 1000 bootstrap samples and find the corresponding 1000 means, do we expect that those 1000 means will target 54.3 seconds or 57.4 seconds? What does that result suggest about the bootstrap method in this case?

Freshman 15 Here is a sample of amounts of weight change (kg) of college students in their freshman year (from Data Set 13 “Freshman 15” in Appendix B): 11, 3, 0, , where represents a loss of 2 kg and positive values represent weight gained. Here are ten bootstrap samples:

[Image]

a. Using only the ten given bootstrap samples, construct an 80% confidence interval estimate of the mean weight change for the population.