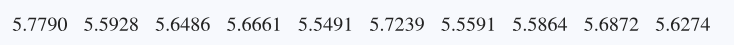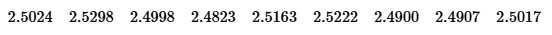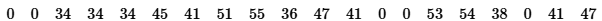Cell Phone Radiation Here is a sample of measured radiation emissions (cW/kg) for cell phones (based on data from the Environmental Working Group): 38, 55, 86, 145. Here are ten bootstrap samples:

[Image]

a. Using only the ten given bootstrap samples, construct an 80% confidence interval estimate of the population mean.

Archeology Archeologists have studied sizes of Egyptian skulls in an attempt to determine whether breeding occurred between different cultures. Listed below are the widths (mm) of skulls from 150 A.D. (based on data from Ancient Races of the Thebaid by Thomson and Randall-Maciver).

a. Use 1000 bootstrap samples to construct a 99% confidence interval estimate of the mean skull width.

Minting Quarters Listed below are weights (grams) of quarters minted after 1964 (based on Data Set 40 “Coin Weights” in Appendix B).

b. Specifications require that the quarters have a weight of 5.670 g. What does the confidence interval suggest about that specification?

Brain Volumes Use these measures of brain volumes from Data Set 12 “IQ and Brain Size” in Appendix B. Use the bootstrap method with 1000 bootstrap samples.

a. Use 1000 bootstrap samples to construct a 90% confidence interval estimate of the population mean.

Analysis of Last Digits Weights of respondents were recorded as part of the California Health Interview Survey. The last digits of weights from 50 randomly selected respondents are listed below.

a. Use the bootstrap method with 1000 bootstrap samples to find a 95% confidence interval estimate of .

7. FRESHMAN 15 Here is a sample of amounts of weight change (kg) of college students in their freshman year (from Data Set 13 “Freshman 15” in Appendix B): 11, 3, 0, –2, where –2 represents a loss of 2 kg and positive values represent weight gained. Here are ten bootstrap samples:

{11, 11, 11, 0}, {11, –2, 0, 11}, {11, –2, 3, 0}, {3, –2, 0, 11}, {0, 0, 0, 3}, {3, –2, 3, –2}, {11, 3, –2, 0}, {–2, 3, –2, 3}, {–2, 0, –2, 3}, {3, 11, 11, 11}.

b. Using only the ten given bootstrap samples, construct an 80% confidence interval estimate of the standard deviation of the weight changes for the population.

15. HEIGHTS OF FEMALE SOCCER PLAYERS Listed below are the heights (in.) of players on the U.S. Women’s National Soccer Team (at the time of this writing). Use those heights as a sample of the heights of all professional women soccer players.

a. Use 1000 bootstrap samples to construct a 95% confidence interval estimate of σ.

Mint Specs Listed below are weights (grams) from a simple random sample of pennies produced after 1983 (from Data Set 40 “Coin Weights” in Appendix B).

b. How does the result compare to the confidence interval found in Exercise 14 in Section 7-3?

Caffeine in Soft Drinks Listed below are measured amounts of caffeine (mg per 12 oz of drink) obtained in one can from each of 20 brands (7UP, A&W Root Beer, Cherry Coke, . . . , TaB).

b. Given that Exercise 20 in Section 7-2 used the same data for a 99% confidence interval based on use of the t distribution, and given that the data do not appear to be from a normally distributed population, which confidence interval is likely to be better: The confidence interval from part (a) or the confidence interval found in Exercise 20 in Section 7-2?

Estimating the Median Use the sample data listed in Exercise 1 “Bootstrap Requirements” to generate 1000 bootstrap samples, and find the median in each of those samples. After obtaining the 1000 sample medians, find the 95% confidence interval estimate of the population median by evaluating p2.5 and p97.5 from the sorted 1000 medians. Given that the sample times in Exercise 1 are from the 50 times in Data Set 20 “Alcohol and Tobacco in Movies” and those 50 times have a median of 5.5, how well did the bootstrap method work to create a “good” confidence interval?

Seating Choice In a 3M Privacy Filters poll, respondents were asked to identify their favorite seat when they fly, and the results include these responses: window, window, other, other. Letting “window” and letting “other”, those four responses can be represented as {1, 1, 0, 0}. Here are ten bootstrap samples for those responses: [Image]

Using only the ten given bootstrap samples, construct an 80% confidence interval estimate of the proportion of respondents who indicated their favorite seat is “window.”

Medical Malpractice In a study of 1228 randomly selected medical malpractice lawsuits, it was found that 856 of them were dropped or dismissed (based on data from the Physicians Insurers Association of America). Use the bootstrap method to construct a 95% confidence interval estimate of the proportion of lawsuits that are dropped or dismissed. Use 1000 bootstrap samples. How does the result compare to the confidence interval found in Exercise 16 “Medical Malpractice” from Section 7-1?

Job Interviews In a Harris poll of 514 human resource professionals, 463 said that the appearance of a job applicant is most important for a good first impression. Use 1000 bootstrap samples to construct a 99% confidence interval estimate of the proportion of all human resource professionals believing that the appearance of a job applicant is most important for a good first impression. How does the result compare to the confidence interval found in Exercise 24 part (b) in Section 7-1?

Sample Size for Proportion Find the sample size required to estimate the percentage of statistics students who take their statistics course online. Assume that we want 95% confidence that the proportion from the sample is within two percentage points of the true population percentage.

Sample Size for Mean Find the sample size required to estimate the mean IQ of airline pilots. Assume that we want 99% confidence that the mean from the sample is within two IQ points of the true population mean. Also assume that sigma=15

Controversial Song The song “Baby It’s Cold Outside” generated much controversy because of its lyrics and tone. CBS New York conducted a survey by asking viewers to use the Internet to respond to a question asking whether that song was really too offensive to play. Among 1043 Internet users who chose to respond, 986 said that the song was not too offensive, and 57 of the respondents said that the song was too offensive.

a. Construct a 95% confidence interval estimate of the proportion of the population having the belief that the song is not too offensive.

Alcohol in Children’s Movies Listed below is a simple random sample of times (seconds) that animated children’s movies showed the use of alcohol (based on Data Set 20 “Alcohol and Tobacco in Movies” in Appendix B).

b. Are the requirements for constructing a 95% confidence interval estimate of the population standard deviation satisfied? If so, construct that confidence interval.