Back
BackProblem 7.1.17
Critical Thinking. In Exercises 17–28, use the data and confidence level to construct a confidence interval estimate of p, then address the given question.
Births A random sample of 860 births in New York State included 426 boys. Construct a 95% confidence interval estimate of the proportion of boys in all births. It is believed that among all births, the proportion of boys is 0.512. Do these sample results provide strong evidence against that belief?
Problem 7.1.21c
Critical Thinking. In Exercises 17–28, use the data and confidence level to construct a confidence interval estimate of p, then address the given question.
Touch Therapy When she was 9 years of age, Emily Rosa did a science fair experiment in which she tested professional touch therapists to see if they could sense her energy field. She flipped a coin to select either her right hand or her left hand, and then she asked the therapists to identify the selected hand by placing their hand just under Emily’s hand without seeing it and without touching it. Among 280 trials, the touch therapists were correct 123 times (based on data in “A Close Look at Therapeutic Touch,” Journal of the American Medical Association, Vol. 279, No. 13).
c. Using Emily’s sample results, construct a 99% confidence interval estimate of the proportion of correct responses made by touch therapists.
Problem 7.1.23a
Critical Thinking. In Exercises 17–28, use the data and confidence level to construct a confidence interval estimate of p, then address the given question.
Job Interviews In a Harris poll of 514 human resource professionals, 45.9% said that body piercings and tattoos were big personal grooming red flags.
a. Among the 514 human resource professionals who were surveyed, how many of them said that body piercings and tattoos were big personal grooming red flags?
Problem 7.1.23c
Critical Thinking. In Exercises 17–28, use the data and confidence level to construct a confidence interval estimate of p, then address the given question.
Job Interviews In a Harris poll of 514 human resource professionals, 45.9% said that body piercings and tattoos were big personal grooming red flags.
c. Repeat part (b) using a confidence level of 80%.
Problem 7.1.24a
Critical Thinking. In Exercises 17–28, use the data and confidence level to construct a confidence interval estimate of p, then address the given question.
Job Interviews In a Harris poll of 514 human resource professionals, 90% said that the appearance of a job applicant is most important for a good first impression.
a. Among the 514 human resource professionals who were surveyed, how many of them said that the appearance of a job applicant is most important for a good first impression?
Problem 7.1.26
Critical Thinking. In Exercises 17–28, use the data and confidence level to construct a confidence interval estimate of p, then address the given question.
Gender Selection Before its clinical trials were discontinued, the Genetics & IVF Institute conducted a clinical trial of the XSORT method designed to increase the probability of conceiving a girl and, among the 945 babies born to parents using the XSORT method, there were 879 girls. The YSORT method was designed to increase the probability of conceiving a boy and, among the 291 babies born to parents using the YSORT method, there were 239 boys. Construct the two 95% confidence interval estimates of the percentages of success. Compare the results. What do you conclude?
Problem 7.1.28
Critical Thinking. In Exercises 17–28, use the data and confidence level to construct a confidence interval estimate of p, then address the given question.
Measured Results vs. Reported Results The same study cited in the preceding exercise produced these results after six months for the 198 patients given sustained care: 25.8% were no longer smoking, and these results were biochemically confirmed, but 40.9% of these patients reported that they were no longer smoking. Construct the two 95% confidence intervals. Compare the results. What do you conclude?
Problem 7.1.29
Heights of Presidents Refer to Data Set 22 “Presidents” in Appendix B. Treat the data as a sample and find the proportion of presidents who were taller than their opponents. Use that result to construct a 95% confidence interval estimate of the population percentage. Based on the result, does it appear that greater height is an advantage for presidential candidates? Why or why not?
Problem 7.1.31b
Wiggle Your Ears Find the sample size needed to estimate the percentage of adults who can wiggle their ears. Use a margin of error of 3 percentage points and use a confidence level of 99%.
b. Assume that 22% of adults can wiggle their ears (based on data from Soul Publishing).
Problem 7.1.32b
Touch Your Nose With Your Tongue Find the sample size needed to estimate the percentage of adults who can touch their nose with their tongue. Use a margin of error of 2 percentage points and use a confidence level of 90%.
b. Assume that a previous study showed that 10% of adults can touch their nose with their tongue (based on data from Onedio).
Problem 7.1.33b
E-Cigarettes A New York Times article reported that a survey conducted in 2014 included 36,000 adults, with 3.7% of them being regular users of e-cigarettes. Because e-cigarette use is relatively new, there is a need to obtain today’s usage rate. How many adults must be surveyed now if we want a confidence level of 95% and a margin of error of 1.5 percentage points?
b. Use the results from the 2014 survey.
Problem 7.1.33c
E-Cigarettes A New York Times article reported that a survey conducted in 2014 included 36,000 adults, with 3.7% of them being regular users of e-cigarettes. Because e-cigarette use is relatively new, there is a need to obtain today’s usage rate. How many adults must be surveyed now if we want a confidence level of 95% and a margin of error of 1.5 percentage points?
c. Does the use of the result from the 2014 survey have much of an effect on the sample size?
Problem 7.1.34a
Astrology A sociologist plans to conduct a survey to estimate the percentage of adults who believe in astrology. How many people must be surveyed if we want a confidence level of 99% and a margin of error of four percentage points?
a. Assume that nothing is known about the percentage to be estimated.
Problem 7.1.34b
Astrology A sociologist plans to conduct a survey to estimate the percentage of adults who believe in astrology. How many people must be surveyed if we want a confidence level of 99% and a margin of error of four percentage points?
b. Use the information from a previous Harris survey in which 26% of respondents said that they believed in astrology.
Problem 7.1.35a
Airline Seating You are the operations manager for American Airlines and you are considering a higher fare level for passengers in aisle seats. You want to estimate the percentage of passengers who now prefer aisle seats. How many randomly selected air passengers must you survey? Assume that you want to be 95% confident that the sample percentage is within 2.5 percentage points of the true population percentage.
a. Assume that nothing is known about the percentage of passengers who prefer aisle seats.
Problem 7.1.36b
Online Gambling Some states now allow online gambling. As a marketing manager for a casino, you need to determine the percentage of adults in those states who gamble online. How many adults must you survey in order to be 99% confident that your estimate is in error by no more than two percentage points?
b. Assume that 18% of all adults gamble online (based on 2017 data from a Gambling Commission study in Great Britain).
Problem 7.1.37a
Smart Phone Apple is planning for the launch of a new and improved iPhone. The marketing team wants to know the worldwide percentage of consumers who intend to purchase the new model, so a survey is being planned. How many people must be surveyed in order to be 90% confident that the estimated percentage is within three percentage points of the true population percentage?
a. Assume that nothing is known about the worldwide percentage of consumers who intend to buy the new model.
Problem 7.1.37b
Smart Phone Apple is planning for the launch of a new and improved iPhone. The marketing team wants to know the worldwide percentage of consumers who intend to purchase the new model, so a survey is being planned. How many people must be surveyed in order to be 90% confident that the estimated percentage is within three percentage points of the true population percentage?
b. Assume that 11% of consumers have a smartphone and plan to upgrade to a new model.
Problem 7.1.37c
Smart Phone Apple is planning for the launch of a new and improved iPhone. The marketing team wants to know the worldwide percentage of consumers who intend to purchase the new model, so a survey is being planned. How many people must be surveyed in order to be 90% confident that the estimated percentage is within three percentage points of the true population percentage?
c. Given that the required sample size is relatively small, could you simply survey the people that you know?
Problem 7.1.38c
Women Who Give Birth An epidemiologist plans to conduct a survey to estimate the percentage of women who give birth. How many women must be surveyed in order to be 99% confident that the estimated percentage is in error by no more than two percentage points?
c. What is wrong with surveying randomly selected adult women?
Problem 7.1.40
One-Sided Confidence Interval A one-sided claim about a population proportion is a claim that the proportion is less than (or greater than) some specific value. Such a claim can be formally addressed using a one-sided confidence interval for p, which can be expressed as p<p+E or p>p-E, where the margin of error E is modified by replacing za/2 with za. (Instead of dividing between two tails of the standard normal distribution, put all of it in one tail.) The Chapter Problem refers to a Sallie Mae survey of 950 undergraduate students, and 53% of the survey subjects take online courses. Use that data to construct a one-sided 95% confidence interval that would be suitable for helping to determine whether the percentage of all undergraduates who take online courses is greater than 50%.
Problem 7.1.33a
E-Cigarettes A New York Times article reported that a survey conducted in 2014 included 36,000 adults, with 3.7% of them being regular users of e-cigarettes. Because e-cigarette use is relatively new, there is a need to obtain today’s usage rate. How many adults must be surveyed now if we want a confidence level of 95% and a margin of error of 1.5 percentage points?
a. Assume that nothing is known about the rate of e-cigarette usage among adults.
Problem 7.1.41a
No Failures According to the Rule of Three, when we have a sample size n with x=0 successes, we have 95% confidence that the true population proportion has an upper bound of 3/n. (See “A Look at the Rule of Three,” by Jovanovic and Levy, American Statistician, Vol. 51, No. 2.)
a. If n independent trials result in no successes, why can’t we find confidence interval limits by using the methods described in this section?
Problem 7.1.42b
No Failures According to the Rule of Three, when we have a sample size n with x=0 successes, we have 95% confidence that the true population proportion has an upper bound of 3/n. (See “A Look at the Rule of Three,” by Jovanovic and Levy, American Statistician, Vol. 51, No. 2.)
b. In a study of failure rates of computer hard drives, 45 Toshiba model MD04ABA500V hard drives were tested and there were no failures. What is the 95% upper bound for the percentage of failures for the population of all such hard drives?
Problem 7.1
Female Motorcycle Owners Here is a 95% confidence interval estimate of the percentage of motorcycle owners who are female: 17.5%<p<20.6% (based on data from the Motorcycle Industry Council). What is the best point estimate of the percentage of motorcycle owners who are women?
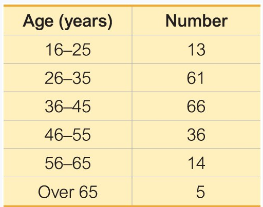
Problem 7.2.33
Ages of Prisoners The accompanying frequency distribution summarizes sample data consisting of ages of randomly selected inmates in federal prisons (based on data from the Federal Bureau of Prisons). Use the data to construct a 95% confidence interval estimate of the mean age of all inmates in federal prisons.
Problem 7.2.34b
Finite Population Correction Factor If a simple random sample of size n is selected without replacement from a finite population of size (n>0.05N), and the sample size is more than 5% of the population size , better results can be obtained by using the finite population correction factor, which involves multiplying the margin of error E by [Image]. Refer to the weights of the M&M candies in Data Set 38 “Candies” in Appendix B.
b. Use only the red M&Ms and treat that sample as a simple random sample selected from the population of the 345 M&Ms listed in the data set. Find the 95% confidence interval estimate of the mean weight of all 345 M&Ms. Compare the result to the actual mean of the population of all 345 M&Ms.
Problem 7.2.7
In Exercises 5–8, (a) identify the critical value ta/2 used for finding the margin of error, (b) find the margin of error, (c) find the confidence interval estimate of u, and (d) write a brief statement that interprets the confidence interval.
Pepsi Weights Here are summary statistics for the weights of Pepsi in randomly selected cans: n=36, x=0.82410 lb, s=0.00570 lb (based on Data Set 37 “Cola Weights and Volumes” in Appendix B). Use a confidence level of 99%.
Problem 7.2.9
Mean Body Temperature Data Set 5 “Body Temperatures” in Appendix B includes a sample of 106 body temperatures having a mean of 98.20 F and a standard deviation of 0.62 F. Construct a 95% confidence interval estimate of the mean body temperature for the entire population. What does the result suggest about the common belief that 98.6 F is the mean body temperature?
Problem 7.2.10
Atkins Weight Loss Program In a test of weight loss programs, 40 adults used the Atkins weight loss program. After 12 months, their mean weight loss was found to be 2.1 lb, with a standard deviation of 4.8 lb. Construct a 90% confidence interval estimate of the mean weight loss for all such subjects. Does the Atkins program appear to be effective? Does it appear to be practical?