Back
BackProblem 6.R.8a
In Exercises 8 and 9, assume that women have standing eye heights that are normally distributed with a mean of 59.7 in. and a standard deviation of 2.5 in. (based on anthropometric survey data from Gordon, Churchill, et al.).
a. If an eye recognition security system is positioned at a height that is uncomfortable for women with standing eye heights less than 54 in., what percentage of women will find that height uncomfortable?
Problem 6.C.1.h
In Exercises 1 and 2, use the following wait times (minutes) at 10:00 AM for the Tower of Terror ride at Disney World (from Data Set 33 “Disney World Wait Times” in Appendix B).
35 35 20 50 95 75 45 50 30 35 30 30
h. Are the wait times discrete data or continuous data?
Problem 6.CRE.2d
In Exercises 1 and 2, use the following wait times (minutes) at 10:00 AM for the Tower of Terror ride at Disney World (from Data Set 33 “Disney World Wait Times” in Appendix B).
35 35 20 50 95 75 45 50 30 35 30 30
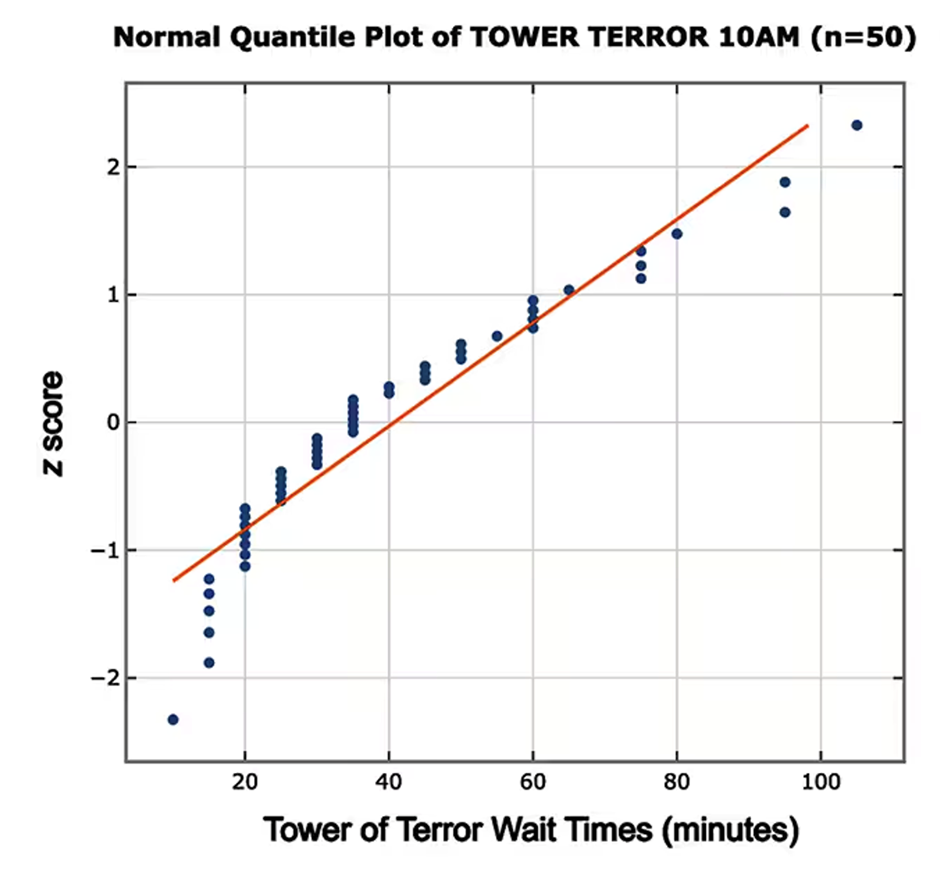
d. The accompanying normal quantile plot is obtained by using all 50 wait times at 10:00 AM for the Tower of Terror ride at Disney World. Based on this normal quantile plot, do the sample data appear to be from a normally distributed population?
Problem 6.CRE.2b
In Exercises 1 and 2, use the following wait times (minutes) at 10:00 AM for the Tower of Terror ride at Disney World (from Data Set 33 “Disney World Wait Times” in Appendix B).
35 35 20 50 95 75 45 50 30 35 30 30
b. Construct a boxplot.
Problem 6.c.2
In Exercises 1 and 2, use the following wait times (minutes) at 10:00 AM for the Tower of Terror ride at Disney World (from Data Set 33 “Disney World Wait Times” in Appendix B).
35 35 20 50 95 75 45 50 30 35 30 30
Tower of Terror Wait Times
a. Find Q1, Q2 and Q3.
Problem 6.CRE.1
In Exercises 1 and 2, use the following wait times (minutes) at 10:00 AM for the Tower of Terror ride at Disney World (from Data Set 33 “Disney World Wait Times” in Appendix B).
35 35 20 50 95 75 45 50 30 35 30 30
a. Find the mean xbar.
Problem 6.CRE.1b
In Exercises 1 and 2, use the following wait times (minutes) at 10:00 AM for the Tower of Terror ride at Disney World (from Data Set 33 “Disney World Wait Times” in Appendix B).
35 35 20 50 95 75 45 50 30 35 30 30
b. Find the median.
Problem 6.c.1c
In Exercises 1 and 2, use the following wait times (minutes) at 10:00 AM for the Tower of Terror ride at Disney World (from Data Set 33 “Disney World Wait Times” in Appendix B).
35 35 20 50 95 75 45 50 30 35 30 30
c. Find the standard deviation s.
Problem 6.c.1d
In Exercises 1 and 2, use the following wait times (minutes) at 10:00 AM for the Tower of Terror ride at Disney World (from Data Set 33 “Disney World Wait Times” in Appendix B).
35 35 20 50 95 75 45 50 30 35 30 30
d. Find the variance.
Problem 6.c.1g
In Exercises 1 and 2, use the following wait times (minutes) at 10:00 AM for the Tower of Terror ride at Disney World (from Data Set 33 “Disney World Wait Times” in Appendix B).
35 35 20 50 95 75 45 50 30 35 30 30
g. What level of measurement (nominal, ordinal, interval, ratio) describes this data set?
Problem 6.CRE.4
Blue Eyes Assume that 35% of us have blue eyes (based on a study by Dr. P. Soria at Indiana University).
b. Find the value of P(B_bar).
Problem 6.CRE.4c
Blue Eyes Assume that 35% of us have blue eyes (based on a study by Dr. P. Soria at Indiana University).
c. Find the probability of randomly selecting three different people and finding that all of them have blue eyes.
Problem 6.CRE.1e
In Exercises 1 and 2, use the following wait times (minutes) at 10:00 AM for the Tower of Terror ride at Disney World (from Data Set 33 “Disney World Wait Times” in Appendix B).
35 35 20 50 95 75 45 50 30 35 30 30
e. Convert the longest wait time to a z score.
f. Based on the result from part (e), is the longest wait time significantly high?
Problem 6.R.1e
Bone Density Test A bone mineral density test is used to identify a bone disease. The result of a bone density test is commonly measured as a z score, and the population of z scores is normally distributed with a mean of 0 and a standard deviation of 1.
e. If the mean bone density test score is found for 9 randomly selected subjects, find the probability that the mean is greater than 0.23.
Problem 6.R.5b
Birth Weights Based on Data Set 6 “Births” in Appendix B, birth weights of girls are normally distributed with a mean of 3037.1 g and a standard deviation of 706.3 g.
b. What is the value of the median?
Problem 6.R.5c
Birth Weights Based on Data Set 6 “Births” in Appendix B, birth weights of girls are normally distributed with a mean of 3037.1 g and a standard deviation of 706.3 g.
c. What is the value of the mode?
Problem 6.R.6a
Mensa Membership in Mensa requires a score in the top 2% on a standard intelligence test. The Wechsler IQ test is designed for a mean of 100 and a standard deviation of 15, and scores are normally distributed.
a. Find the minimum Wechsler IQ test score that satisfies the Mensa requirement.
Problem 6.R.6b
Mensa Membership in Mensa requires a score in the top 2% on a standard intelligence test. The Wechsler IQ test is designed for a mean of 100 and a standard deviation of 15, and scores are normally distributed.
b. If 4 randomly selected adults take the Wechsler IQ test, find the probability that their mean score is at least 131.
Problem 6.R.9
In Exercises 8 and 9, assume that women have standing eye heights that are normally distributed with a mean of 59.7 in. and a standard deviation of 2.5 in. (based on anthropometric survey data from Gordon, Churchill, et al.).
Significance Instead of using 0.05 for identifying significant values, use the criteria that a value x is significantly high if P(x or greater) ≤ 0.01 and a value is significantly low if P(x or less) ≤ 0.01. Find the standing eye heights of women that separate significant values from those that are not significant. Using these criteria, is a woman’s standing eye height of 67 in. significantly high?
Problem 6.CR.3a
Foot Lengths of Women Assume that foot lengths of adult females are normally distributed with a mean of 246.3 mm and a standard deviation of 12.4 mm (based on Data Set 3 “ANSUR II 2012” in Appendix B).
a. Find the probability that a randomly selected adult female has a foot length less than 221.5 mm.
Problem 6.CR.3c
Foot Lengths of Women Assume that foot lengths of adult females are normally distributed with a mean of 246.3 mm and a standard deviation of 12.4 mm (based on Data Set 3 “ANSUR II 2012” in Appendix B).
c. Find P95.
Problem 6.CR.7a
Normal Distribution Using a larger data set than the one given for the preceding exercises, assume that cell phone radiation amounts are normally distributed with a mean of 1.17 W/kg and a standard deviation of 0.29 W/kg.
a. Find the probability that a randomly selected cell phone has a radiation amount that exceeds the U.S. standard of 1.6 W/kg or less.
Problem 6.q.2
Bone Density Test. In Exercises 1–4, assume that scores on a bone mineral density test are normally distributed with a mean of 0 and a standard deviation of 1.
Bone Density Find the bone density score that is the 90th percentile, which is the score separating the lowest 90% from the top 10%.
Problem 6.q.4
Bone Density Test. In Exercises 1–4, assume that scores on a bone mineral density test are normally distributed with a mean of 0 and a standard deviation of 1.
Bone Density For a randomly selected subject, find the probability of a bone density score between and 2.00.
Problem 6.q.7
Seat Designs. In Exercises 7–9, assume that when seated, adult males have back-to-knee lengths that are normally distributed with a mean of 23.5 in. and a standard deviation of 1.1 in. (based on anthropometric survey data from Gordon, Churchill, et al.). These data are used often in the design of different seats, including aircraft seats, train seats, theater seats, and classroom seats.
Find the probability that a male has a back-to-knee length greater than 25.0 in.
Problem 6.q.9
Seat Designs. In Exercises 7–9, assume that when seated, adult males have back-to-knee lengths that are normally distributed with a mean of 23.5 in. and a standard deviation of 1.1 in. (based on anthropometric survey data from Gordon, Churchill, et al.). These data are used often in the design of different seats, including aircraft seats, train seats, theater seats, and classroom seats.
Find the probability that nine males have back-to-knee lengths with a mean greater than 23.0 in.
Problem 6.r.1a
Bone Density Test A bone mineral density test is used to identify a bone disease. The result of a bone density test is commonly measured as a z score, and the population of z scores is normally distributed with a mean of 0 and a standard deviation of 1.
a. For a randomly selected subject, find the probability of a bone density test score greater than -1.37.
Problem 6.r.1c
Bone Density Test A bone mineral density test is used to identify a bone disease. The result of a bone density test is commonly measured as a z score, and the population of z scores is normally distributed with a mean of 0 and a standard deviation of 1.
c. For a randomly selected subject, find the probability of a bone density test score between -0.67 and 1.29.
Problem 6.R.4b
Arm Circumferences Arm circumferences of adult men are normally distributed with a mean of 33.64 cm and a standard deviation of 4.14 cm (based on Data Set 1 “Body Data” in Appendix B). A sample of 25 men is randomly selected and the mean of the arm circumferences is obtained.
b. What is the mean of all such sample means?
Problem 6.CRE.3d
Foot Lengths of Women Assume that foot lengths of adult females are normally distributed with a mean of 246.3 mm and a standard deviation of 12.4 mm (based on Data Set 3 “ANSUR II 2012” in Appendix B).
d. Find the probability that 16 adult females have foot lengths with a mean greater than 250 mm.