Here are the essential concepts you must grasp in order to answer the question correctly.
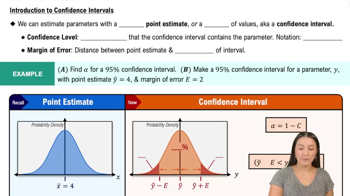
Confidence Interval
A confidence interval is a range of values, derived from sample statistics, that is likely to contain the true population parameter. In this context, a 98% confidence level indicates that if we were to take many samples, approximately 98% of the calculated intervals would contain the true mean IQ of data scientists. This concept is crucial for understanding how sample size affects the precision of our estimates.
Recommended video:
Introduction to Confidence Intervals
Sample Size Calculation
Sample size calculation involves determining the number of observations needed to achieve a desired level of precision in estimating a population parameter. The formula typically incorporates the desired confidence level, the population standard deviation (sigma), and the margin of error. In this case, we need to calculate how many data scientists' IQ scores are required to ensure that our estimate is within 2 IQ points of the true mean with 98% confidence.
Recommended video:
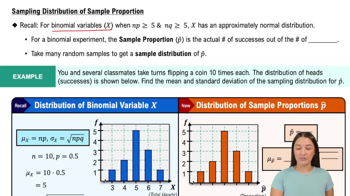
Sampling Distribution of Sample Proportion
Standard Deviation
Standard deviation is a measure of the amount of variation or dispersion in a set of values. In this scenario, the population standard deviation (sigma = 15) indicates how much individual IQ scores of data scientists deviate from the mean. Understanding standard deviation is essential for calculating the sample size, as it influences the width of the confidence interval and the required sample size for a given margin of error.
Recommended video:
Calculating Standard Deviation