Construct a 95% confidence interval for the mean difference of the population given the following information. Would you reject or fail to reject the claim that there is no difference in the mean?
Table of contents
- 1. Introduction to Statistics53m
- 2. Describing Data with Tables and Graphs2h 1m
- 3. Describing Data Numerically2h 8m
- 4. Probability2h 26m
- 5. Binomial Distribution & Discrete Random Variables3h 28m
- 6. Normal Distribution & Continuous Random Variables2h 21m
- 7. Sampling Distributions & Confidence Intervals: Mean3h 37m
- Sampling Distribution of the Sample Mean and Central Limit Theorem19m
- Distribution of Sample Mean - Excel23m
- Introduction to Confidence Intervals22m
- Confidence Intervals for Population Mean1h 26m
- Determining the Minimum Sample Size Required12m
- Finding Probabilities and T Critical Values - Excel28m
- Confidence Intervals for Population Means - Excel25m
- 8. Sampling Distributions & Confidence Intervals: Proportion1h 33m
- 9. Hypothesis Testing for One Sample3h 32m
- 10. Hypothesis Testing for Two Samples4h 49m
- Two Proportions1h 12m
- Two Proportions Hypothesis Test - Excel28m
- Two Means - Unknown, Unequal Variance1h 2m
- Two Means - Unknown Variances Hypothesis Test - Excel12m
- Two Means - Unknown, Equal Variance15m
- Two Means - Unknown, Equal Variances Hypothesis Test - Excel9m
- Two Means - Known Variance12m
- Two Means - Sigma Known Hypothesis Test - Excel21m
- Two Means - Matched Pairs (Dependent Samples)42m
- Matched Pairs Hypothesis Test - Excel12m
- 11. Correlation1h 24m
- 12. Regression1h 59m
- 13. Chi-Square Tests & Goodness of Fit2h 31m
- 14. ANOVA2h 1m
10. Hypothesis Testing for Two Samples
Two Means - Matched Pairs (Dependent Samples)
Struggling with Statistics for Business?
Join thousands of students who trust us to help them ace their exams!Watch the first videoMultiple Choice
A personal trainer is studying whether a new stretching routine improves flexibility. She records the forward reach (in cm) of 6 clients before and after a 4-week program. Calculate the difference (after - before) for each client, the mean difference, and standard deviation.
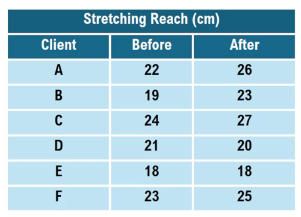
A
Difference for each client: A=4,B=4,C=3,D=−1,E=0,F=2; The Mean Difference = 2; and Standard Deviation = 1.91
B
Difference for each client: A=4,B=4,C=3,D=−1,E=0,F=2; The Mean Difference = 2.5; and Standard Deviation = 1.91
C
Difference for each client: A=4,B=4,C=3,D=−1,E=0,F=2; The Mean Difference = 2.5; and Standard Deviation = 2.10
D
Difference for each client: A=4,B=4,C=3,D=−1,E=0,F=2; The Mean Difference = 2; and Standard Deviation = 2.10
 Verified step by step guidance
Verified step by step guidance1
Step 1: Calculate the difference (After - Before) for each client. Use the values from the table: Client A: 26 - 22 = 4, Client B: 23 - 19 = 4, Client C: 27 - 24 = 3, Client D: 20 - 21 = -1, Client E: 18 - 18 = 0, Client F: 25 - 23 = 2.
Step 2: Compute the mean difference. Add all the differences calculated in Step 1 (4 + 4 + 3 - 1 + 0 + 2) and divide by the number of clients (6). The formula for mean difference is: , where d represents the differences and n is the number of clients.
Step 3: Calculate the squared deviations from the mean for each difference. For each client, subtract the mean difference from their individual difference, then square the result. The formula is: .
Step 4: Compute the variance. Add all the squared deviations calculated in Step 3 and divide by the number of clients minus 1 (n - 1). The formula for variance is: .
Step 5: Calculate the standard deviation. Take the square root of the variance calculated in Step 4. The formula for standard deviation is: .

 8:33m
8:33mWatch next
Master Introduction to Matched Pairs with a bite sized video explanation from Patrick
Start learningRelated Videos
Related Practice
Two Means - Matched Pairs (Dependent Samples) practice set


