Multiple Choice
Find the area under the standard normal distribution to the left of a z-score of .
6. Normal Distribution & Continuous Random Variables
Standard Normal Distribution
Struggling with Statistics for Business?
Join thousands of students who trust us to help them ace their exams!Watch the first videoMultiple Choice
Find the z-score corresponding to the probability/area shown under the standard normal curve below.
A
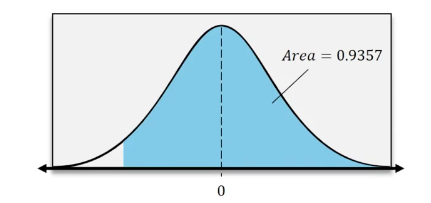
-1.52
B
1.52
C
0.82
D
-0.82
Verified step by step guidance1
Understand that the z-score is a measure of how many standard deviations an element is from the mean. In a standard normal distribution, the mean is 0 and the standard deviation is 1.
Recognize that the area under the standard normal curve represents the cumulative probability. The area given is 0.9357, which is the probability that a value is less than the z-score we are looking for.
To find the z-score corresponding to a cumulative probability of 0.9357, you can use a standard normal distribution table (z-table) or a statistical software that provides the inverse cumulative distribution function.
Locate the probability value of 0.9357 in the z-table. The z-score is the value that corresponds to this cumulative probability. If using software, input the cumulative probability to get the z-score.
Interpret the z-score: If the z-score is positive, it indicates the value is above the mean; if negative, it indicates the value is below the mean. The options provided suggest possible z-scores, and you can match the calculated z-score to these options.
9:47mWatch next
Master Finding Standard Normal Probabilities using z-Table with a bite sized video explanation from Patrick
Start learningRelated Videos
Related Practice