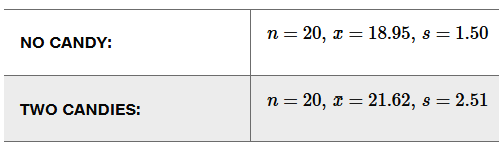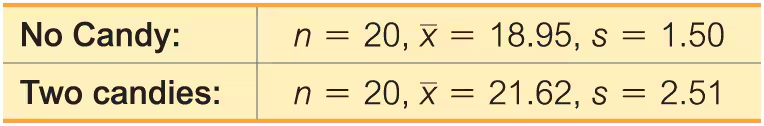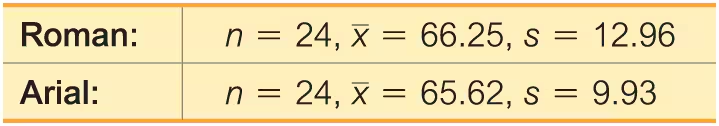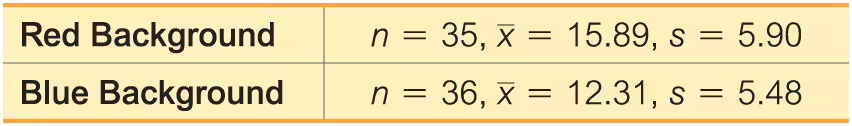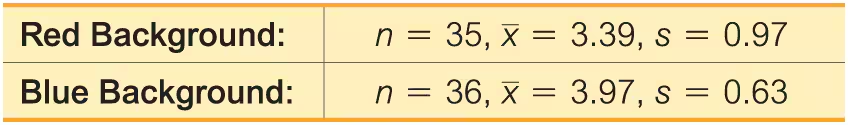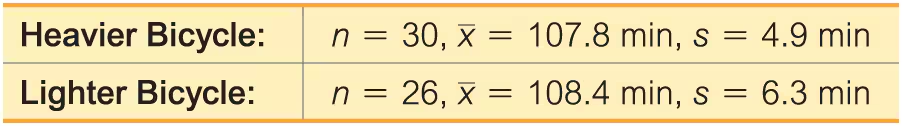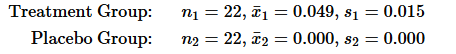Clinical Trials of OxyContin OxyContin (oxycodone) is a drug used to treat pain, but it is well known for its addictiveness and danger. In a clinical trial, among subjects treated with OxyContin, 52 developed nausea and 175 did not develop nausea. Among other subjects given placebos, 5 developed nausea and 40 did not develop nausea (based on data from Purdue Pharma L.P.). Use a 0.05 significance level to test for a difference between the rates of nausea for those treated with OxyContin and those given a placebo.

c. Does nausea appear to be an adverse reaction resulting from OxyContin?

Pulse Rates of Women and Men Using the samples of women and men included in Data Set 1 “Body Data,” we get this 95% confidence interval estimate of the difference between the population mean of pulse rates (bpm) of women and the population mean of pulse rates (bpm) of men: 1.7 bpm < u1-u2 < 7.2bpm. In this confidence interval, women correspond to population 1 and men correspond to population 2.

a. What does the confidence interval suggest about equality of the mean pulse rate of women and the mean pulse rate of men?

Degrees of Freedom For Example 1, we used df=smaller of n1-1 and n2-1 we got df=11 and the corresponding critical value is t=-1.796 (found from Table A-4). If we calculate df using Formula 9-1, we get df=19.370 and the corresponding critical value is t=-1.727 How is using the critical value of t=-1.796 “more conservative” than using the critical value of t=-1.727

In Exercises 5–20, assume that the two samples are independent simple random samples selected from normally distributed populations, and do not assume that the population standard deviations are equal. (Note: Answers in Appendix D include technology answers based on Formula 9-1 along with “Table” answers based on Table A-3 with df equal to the smaller of n1-1 and n2-1)

Better Tips by Giving Candy An experiment was conducted to determine whether giving candy to dining parties resulted in greater tips. The mean tip percentages and standard deviations are given below along with the sample sizes (based on data from “Sweetening the Till: The Use of Candy to Increase Restaurant Tipping,” by Strohmetz et al., Journal of Applied Social Psychology, Vol. 32, No. 2).

a. Use a 0.05 significance level to test the claim that giving candy does result in greater tips.

[Image]

Independent Samples Which of the following involve independent samples?

a. Data Set 4 “Measured and Reported” includes measured heights matched with the heights that were reported when the subjects were asked for those values.

Independent Samples Which of the following involve independent samples?

b. Data Set 6 “Births” includes birth weights of a sample of baby boys and a sample of baby girls.

Independent Samples Which of the following involve independent samples?

c. Data Set 1 “Body Data” includes a sample of pulse rates of 147 women and a sample of pulse rates of 153 men.

Degrees of Freedom In Exercise 20 “Blanking Out on Tests,” using the “smaller of n1-1 and n2-1” for the number of degrees of freedom results in df=15 Find the number of degrees of freedom using Formula 9-1. In general, how are hypothesis tests and confidence intervals affected by using Formula 9-1 instead of the “smaller of n1-1 and n2-1 ”?

In Exercises 5–20, assume that the two samples are independent simple random samples selected from normally distributed populations, and do not assume that the population standard deviations are equal. (Note: Answers in Appendix D include technology answers based on Formula 9-1 along with “Table” answers based on Table A-3 with df equal to the smaller of n1-1 and n2-1)

Better Tips by Giving Candy An experiment was conducted to determine whether giving candy to dining parties resulted in greater tips. The mean tip percentages and standard deviations are given below along with the sample sizes (based on data from “Sweetening the Till: The Use of Candy to Increase Restaurant Tipping,” by Strohmetz et al., Journal of Applied Social Psychology, Vol. 32, No. 2).

b. Construct the confidence interval suitable for testing the claim in part (a).

In Exercises 5–20, assume that the two samples are independent simple random samples selected from normally distributed populations, and do not assume that the population standard deviations are equal. (Note: Answers in Appendix D include technology answers based on Formula 9-1 along with “Table” answers based on Table A-3 with df equal to the smaller of n1-1 and n2-1)

Readability of Font On a Computer Screen The statistics shown below were obtained from a standard test of readability of fonts on a computer screen (based on data from “Reading on the Computer Screen: Does Font Type Have Effects on Web Text Readability?” by Ali et al., International Education Studies, Vol. 6, No. 3). Reading speed and accuracy were combined into a readability performance score (x), where a higher score represents better font readability.

a. Use a 0.05 significance level to test the claim that there is no significant difference in readability between Roman and Arial fonts.

In Exercises 5–20, assume that the two samples are independent simple random samples selected from normally distributed populations, and do not assume that the population standard deviations are equal. (Note: Answers in Appendix D include technology answers based on Formula 9-1 along with “Table” answers based on Table A-3 with df equal to the smaller of n1-1 and n2-1)

Readability of Font On a Computer Screen The statistics shown below were obtained from a standard test of readability of fonts on a computer screen (based on data from “Reading on the Computer Screen: Does Font Type Have Effects on Web Text Readability?” by Ali et al., International Education Studies, Vol. 6, No. 3). Reading speed and accuracy were combined into a readability performance score (x), where a higher score represents better font readability.

b. Construct the confidence interval suitable for testing the claim in part (a).

In Exercises 5–20, assume that the two samples are independent simple random samples selected from normally distributed populations, and do not assume that the population standard deviations are equal. (Note: Answers in Appendix D include technology answers based on Formula 9-1 along with “Table” answers based on Table A-3 with df equal to the smaller of n1-1 and n2-1)

Color and Cognition Researchers from the University of British Columbia conducted a study to investigate the effects of color on cognitive tasks. Words were displayed on a computer screen with background colors of red and blue. Results from scores on a test of word recall are given below. Higher scores correspond to greater word recall.

a. Use a 0.05 significance level to test the claim that the samples are from populations with the same mean.

In Exercises 5–20, assume that the two samples are independent simple random samples selected from normally distributed populations, and do not assume that the population standard deviations are equal. (Note: Answers in Appendix D include technology answers based on Formula 9-1 along with “Table” answers based on Table A-3 with df equal to the smaller of n1-1 and n2-1)

Color and Cognition Researchers from the University of British Columbia conducted a study to investigate the effects of color on cognitive tasks. Words were displayed on a computer screen with background colors of red and blue. Results from scores on a test of word recall are given below. Higher scores correspond to greater word recall.

b. Construct a confidence interval appropriate for the hypothesis test in part (a). What is it about the confidence interval that causes us to reach the same conclusion from part (a)?

In Exercises 5–20, assume that the two samples are independent simple random samples selected from normally distributed populations, and do not assume that the population standard deviations are equal. (Note: Answers in Appendix D include technology answers based on Formula 9-1 along with “Table” answers based on Table A-3 with df equal to the smaller of n1-1 and n2-1)

Color and Cognition Researchers from the University of British Columbia conducted a study to investigate the effects of color on cognitive tasks. Words were displayed on a computer screen with background colors of red and blue. Results from scores on a test of word recall are given below. Higher scores correspond to greater word recall.

c. Does the background color appear to have an effect on word recall scores? If so, which color appears to be associated with higher word memory recall scores?

In Exercises 5–20, assume that the two samples are independent simple random samples selected from normally distributed populations, and do not assume that the population standard deviations are equal. (Note: Answers in Appendix D include technology answers based on Formula 9-1 along with “Table” answers based on Table A-3 with df equal to the smaller of n1-1 and n2-1)

Color and Creativity Researchers from the University of British Columbia conducted trials to investigate the effects of color on creativity. Subjects with a red background were asked to think of creative uses for a brick; other subjects with a blue background were given the same task. Responses were scored by a panel of judges and results from scores of creativity are given below. Higher scores correspond to more creativity. The researchers make the claim that “blue enhances performance on a creative task.”

a. Use a 0.01 significance level to test the claim that blue enhances performance on a creative task.

In Exercises 5–20, assume that the two samples are independent simple random samples selected from normally distributed populations, and do not assume that the population standard deviations are equal. (Note: Answers in Appendix D include technology answers based on Formula 9-1 along with “Table” answers based on Table A-3 with df equal to the smaller of n1-1 and n2-1)

Color and Creativity Researchers from the University of British Columbia conducted trials to investigate the effects of color on creativity. Subjects with a red background were asked to think of creative uses for a brick; other subjects with a blue background were given the same task. Responses were scored by a panel of judges and results from scores of creativity are given below. Higher scores correspond to more creativity. The researchers make the claim that “blue enhances performance on a creative task.”

b. Construct the confidence interval appropriate for the hypothesis test in part (a). What is it about the confidence interval that causes us to reach the same conclusion from part (a)?

In Exercises 5–20, assume that the two samples are independent simple random samples selected from normally distributed populations, and do not assume that the population standard deviations are equal. (Note: Answers in Appendix D include technology answers based on Formula 9-1 along with “Table” answers based on Table A-3 with df equal to the smaller of n1-1 and n2-1)

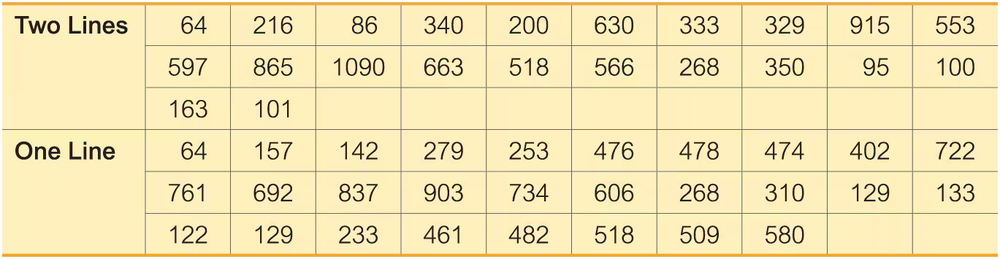
Queues Listed on the next page are waiting times (seconds) of observed cars at a Delaware inspection station. The data from two waiting lines are real observations, and the data from the single waiting line are modeled from those real observations. These data are from Data Set 30 “Queues” in Appendix B. The data were collected by the author.

b. Construct the confidence interval suitable for testing the claim in part (a).

In Exercises 5–20, assume that the two samples are independent simple random samples selected from normally distributed populations, and do not assume that the population standard deviations are equal. (Note: Answers in Appendix D include technology answers based on Formula 9-1 along with “Table” answers based on Table A-3 with df equal to the smaller of n1-1 and n2-1)

Queues Listed on the next page are waiting times (seconds) of observed cars at a Delaware inspection station. The data from two waiting lines are real observations, and the data from the single waiting line are modeled from those real observations. These data are from Data Set 30 “Queues” in Appendix B. The data were collected by the author.

a. Use a 0.01 significance level to test the claim that cars in two queues have a mean waiting time equal to that of cars in a single queue.

In Exercises 5–20, assume that the two samples are independent simple random samples selected from normally distributed populations, and do not assume that the population standard deviations are equal. (Note: Answers in Appendix D include technology answers based on Formula 9-1 along with “Table” answers based on Table A-3 with df equal to the smaller of n1-1 and n2-1)

Bicycle Commuting A researcher used two different bicycles to commute to work. One bicycle was steel and weighed 30.0 lb; the other was carbon and weighed 20.9 lb. The commuting times (minutes) were recorded with the results shown below (based on data from “Bicycle Weights and Commuting Time,” by Jeremy Groves, British Medical Journal).

b. Construct the confidence interval suitable for testing the claim in part (a).

In Exercises 5–20, assume that the two samples are independent simple random samples selected from normally distributed populations, and do not assume that the population standard deviations are equal. (Note: Answers in Appendix D include technology answers based on Formula 9-1 along with “Table” answers based on Table A-3 with df equal to the smaller of n1-1 and n2-1)

Bicycle Commuting A researcher used two different bicycles to commute to work. One bicycle was steel and weighed 30.0 lb; the other was carbon and weighed 20.9 lb. The commuting times (minutes) were recorded with the results shown below (based on data from “Bicycle Weights and Commuting Time,” by Jeremy Groves, British Medical Journal).

a. Use a 0.05 significance level to test the claim that the mean commuting time with the heavier bicycle is the same as the mean commuting time with the lighter bicycle.

In Exercises 5–20, assume that the two samples are independent simple random samples selected from normally distributed populations, and do not assume that the population standard deviations are equal. (Note: Answers in Appendix D include technology answers based on Formula 9-1 along with “Table” answers based on Table A-3 with df equal to the smaller of n1-1 and n2-1)

Magnet Treatment of Pain People spend around $5 billion annually for the purchase of magnets used to treat a wide variety of pains. Researchers conducted a study to determine whether magnets are effective in treating back pain. Pain was measured using the visual analog scale, and the results given below are among the results obtained in the study (based on data from “Bipolar Permanent Magnets for the Treatment of Chronic Lower Back Pain: A Pilot Study,” by Collacott, Zimmerman, White, and Rindone, Journal of the American Medical Association, Vol. 283, No. 10). Higher scores correspond to greater pain levels.

c. Does it appear that magnets are effective in treating back pain? Is it valid to argue that magnets might appear to be effective if the sample sizes are larger?

In Exercises 5–20, assume that the two samples are independent simple random samples selected from normally distributed populations, and do not assume that the population standard deviations are equal. (Note: Answers in Appendix D include technology answers based on Formula 9-1 along with “Table” answers based on Table A-3 with df equal to the smaller of n1-1 and n2-1)

Magnet Treatment of Pain People spend around $5 billion annually for the purchase of magnets used to treat a wide variety of pains. Researchers conducted a study to determine whether magnets are effective in treating back pain. Pain was measured using the visual analog scale, and the results given below are among the results obtained in the study (based on data from “Bipolar Permanent Magnets for the Treatment of Chronic Lower Back Pain: A Pilot Study,” by Collacott, Zimmerman, White, and Rindone, Journal of the American Medical Association, Vol. 283, No. 10). Higher scores correspond to greater pain levels.

b. Construct the confidence interval appropriate for the hypothesis test in part (a).

In Exercises 5–20, assume that the two samples are independent simple random samples selected from normally distributed populations, and do not assume that the population standard deviations are equal. (Note: Answers in Appendix D include technology answers based on Formula 9-1 along with “Table” answers based on Table A-3 with df equal to the smaller of n1-1 and n2-1)

Magnet Treatment of Pain People spend around $5 billion annually for the purchase of magnets used to treat a wide variety of pains. Researchers conducted a study to determine whether magnets are effective in treating back pain. Pain was measured using the visual analog scale, and the results given below are among the results obtained in the study (based on data from “Bipolar Permanent Magnets for the Treatment of Chronic Lower Back Pain: A Pilot Study,” by Collacott, Zimmerman, White, and Rindone, Journal of the American Medical Association, Vol. 283, No. 10). Higher scores correspond to greater pain levels.

a. Use a 0.05 significance level to test the claim that those treated with magnets have a greater mean reduction in pain than those given a sham treatment (similar to a placebo).

No Variation in a Sample An experiment was conducted to test the effects of alcohol. Researchers measured the breath alcohol levels for a treatment group of people who drank ethanol and another group given a placebo. The results are given below (based on data from “Effects of Alcohol Intoxication on Risk Taking, Strategy, and Error Rate in Visuomotor Performance,” by Streufert et al., Journal of Applied Psychology, Vol. 77, No. 4). Use a 0.05 significance level to test the claim that the two sample groups come from populations with the same mean.

Confidence Interval Assume that we want to use the sample data in Exercise 1 for constructing a confidence interval to be used for testing the given claim.

c. If the resulting confidence interval is -5.8 admissions <ud < -0.9 admissions, what do you conclude?

In Exercises 5–16, use the listed paired sample data, and assume that the samples are simple random samples and that the differences have a distribution that is approximately normal.

Heights of Presidents A popular theory is that presidential candidates have an advantage if they are taller than their main opponents. Listed are heights (cm) of presidents along with the heights of their main opponents (from Data Set 22 “Presidents” in Appendix B).

a. Use the sample data with a 0.05 significance level to test the claim that for the population of heights of presidents and their main opponents, the differences have a mean greater than 0 cm.

In Exercises 5–16, use the listed paired sample data, and assume that the samples are simple random samples and that the differences have a distribution that is approximately normal.

The Freshman 15 The “Freshman 15” refers to the belief that college students gain 15 lb (or 6.8 kg) during their freshman year. Listed below are weights (kg) of randomly selected male college freshmen (from Data Set 13 “Freshman 15” in Appendix B). The weights were measured in September and later in April.

c. What do you conclude about the Freshman 15 belief?

In Exercises 5–16, use the listed paired sample data, and assume that the samples are simple random samples and that the differences have a distribution that is approximately normal.

The Freshman 15 The “Freshman 15” refers to the belief that college students gain 15 lb (or 6.8 kg) during their freshman year. Listed below are weights (kg) of randomly selected male college freshmen (from Data Set 13 “Freshman 15” in Appendix B). The weights were measured in September and later in April.

b. Construct the confidence interval that could be used for the hypothesis test described in part (a). What feature of the confidence interval leads to the same conclusion reached in part (a)?

In Exercises 5–16, use the listed paired sample data, and assume that the samples are simple random samples and that the differences have a distribution that is approximately normal.

The Freshman 15 The “Freshman 15” refers to the belief that college students gain 15 lb (or 6.8 kg) during their freshman year. Listed below are weights (kg) of randomly selected male college freshmen (from Data Set 13 “Freshman 15” in Appendix B). The weights were measured in September and later in April.

a. Use a 0.01 significance level to test the claim that for the population of freshman male college students, the weights in September are less than the weights in the following April.

In Exercises 5–16, use the listed paired sample data, and assume that the samples are simple random samples and that the differences have a distribution that is approximately normal.

Do Men Talk Less than Women? Listed below are word counts of males and females in couple relationships (from Data Set 14 “Word Counts” in Appendix B).

b. Construct the confidence interval that could be used for the hypothesis test described in part (a). What feature of the confidence interval leads to the same conclusion reached in part (a)?