Good Sample? An economist is investigating the incomes of college students. Because she lives in Maine, she obtains sample data from that state. Is the resulting mean income of college students a good estimator of the mean income of college students in the United States? Why or why not?
Table of contents
- 1. Intro to Stats and Collecting Data1h 14m
- 2. Describing Data with Tables and Graphs1h 55m
- 3. Describing Data Numerically2h 5m
- 4. Probability2h 16m
- 5. Binomial Distribution & Discrete Random Variables3h 6m
- 6. Normal Distribution and Continuous Random Variables2h 11m
- 7. Sampling Distributions & Confidence Intervals: Mean3h 23m
- Sampling Distribution of the Sample Mean and Central Limit Theorem19m
- Distribution of Sample Mean - Excel23m
- Introduction to Confidence Intervals15m
- Confidence Intervals for Population Mean1h 18m
- Determining the Minimum Sample Size Required12m
- Finding Probabilities and T Critical Values - Excel28m
- Confidence Intervals for Population Means - Excel25m
- 8. Sampling Distributions & Confidence Intervals: Proportion1h 12m
- 9. Hypothesis Testing for One Sample3h 29m
- 10. Hypothesis Testing for Two Samples4h 50m
- Two Proportions1h 13m
- Two Proportions Hypothesis Test - Excel28m
- Two Means - Unknown, Unequal Variance1h 3m
- Two Means - Unknown Variances Hypothesis Test - Excel12m
- Two Means - Unknown, Equal Variance15m
- Two Means - Unknown, Equal Variances Hypothesis Test - Excel9m
- Two Means - Known Variance12m
- Two Means - Sigma Known Hypothesis Test - Excel21m
- Two Means - Matched Pairs (Dependent Samples)42m
- Matched Pairs Hypothesis Test - Excel12m
- 11. Correlation1h 6m
- 12. Regression1h 50m
- 13. Chi-Square Tests & Goodness of Fit1h 57m
- 14. ANOVA1h 57m
7. Sampling Distributions & Confidence Intervals: Mean
Introduction to Confidence Intervals
Problem 9.2.4
Textbook Question
Degrees of Freedom For Example 1, we used df=smaller of n1-1 and n2-1 we got df=11 and the corresponding critical value is t=-1.796 (found from Table A-4). If we calculate df using Formula 9-1, we get df=19.370 and the corresponding critical value is t=-1.727 How is using the critical value of t=-1.796 “more conservative” than using the critical value of t=-1.727
 Verified step by step guidance
Verified step by step guidance1
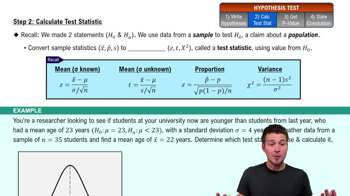
Step 1: Understand the concept of degrees of freedom (df). Degrees of freedom represent the number of independent values or quantities that can vary in a statistical calculation. In this problem, df is calculated using two methods: the smaller of n1-1 and n2-1, and Formula 9-1.
Step 2: Recognize the relationship between degrees of freedom and the critical value of t. A smaller df typically results in a larger critical value of t, which corresponds to a wider confidence interval or stricter threshold for rejecting the null hypothesis.
Step 3: Compare the two critical values provided: t = -1.796 (using df = 11) and t = -1.727 (using df = 19.370). The critical value of t = -1.796 is larger in magnitude, meaning it sets a stricter threshold for statistical significance.
Step 4: Understand the term 'more conservative.' In statistics, a 'more conservative' approach means being less likely to reject the null hypothesis. Using the larger critical value (t = -1.796) requires stronger evidence to reject the null hypothesis, making this approach more conservative.
Step 5: Conclude that using the smaller df (df = 11) and the corresponding critical value of t = -1.796 is more conservative because it increases the likelihood of retaining the null hypothesis, reducing the risk of Type I error (false positive).
 Verified video answer for a similar problem:
Verified video answer for a similar problem:This video solution was recommended by our tutors as helpful for the problem above
Video duration:
4mPlay a video:
Was this helpful?
Key Concepts
Here are the essential concepts you must grasp in order to answer the question correctly.
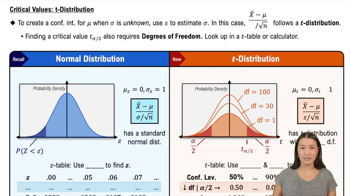
Degrees of Freedom
Degrees of freedom (df) refer to the number of independent values or quantities that can vary in a statistical calculation. In hypothesis testing, df is crucial for determining the appropriate distribution to use, as it affects the shape of the t-distribution. The smaller the df, the wider the t-distribution, which can lead to more conservative estimates in statistical tests.
Recommended video:
Critical Values: t-Distribution
Critical Value
A critical value is a threshold that determines the boundary for rejecting the null hypothesis in hypothesis testing. It is derived from the chosen significance level (alpha) and the relevant statistical distribution, such as the t-distribution. In this context, a more conservative critical value means that it is less likely to reject the null hypothesis, thus reducing the risk of Type I errors.
Recommended video:

Critical Values: t-Distribution
Conservativeness in Statistical Testing
In statistical testing, a conservative approach refers to using stricter criteria for making decisions, such as requiring stronger evidence to reject the null hypothesis. This is often achieved by using a higher critical value, which leads to a lower probability of falsely rejecting the null hypothesis. In the given example, using the critical value of t=-1.796 is more conservative than t=-1.727, as it requires more substantial evidence to conclude a significant effect.
Recommended video:
Guided course
Step 2: Calculate Test Statistic

 6:33m
6:33mWatch next
Master Introduction to Confidence Intervals with a bite sized video explanation from Patrick
Start learningRelated Videos
Related Practice
Textbook Question
