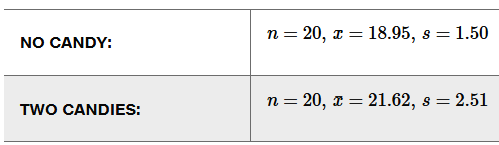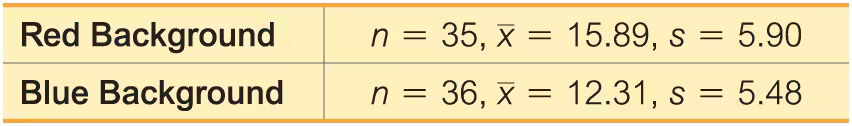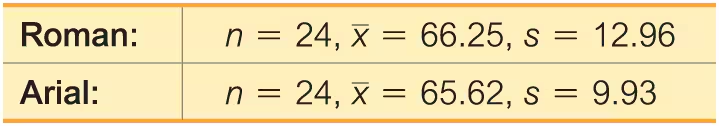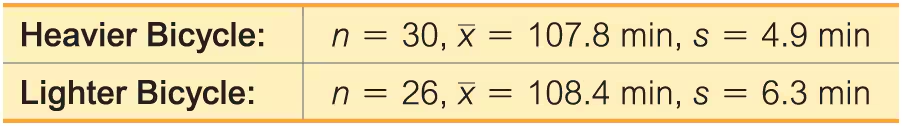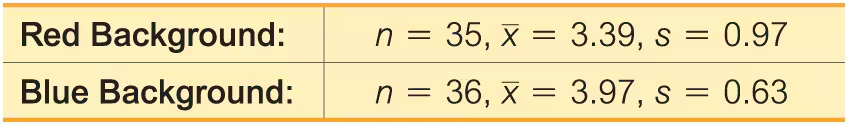Smoking Cessation Programs Among 198 smokers who underwent a “sustained care” program, 51 were no longer smoking after six months. Among 199 smokers who underwent a “standard care” program, 30 were no longer smoking after six months (based on data from “Sustained Care Intervention and Postdischarge Smoking Cessation Among Hospitalized Adults,” by Rigotti et al., Journal of the American Medical Association, Vol. 312, No. 7). We want to use a 0.01 significance level to test the claim that the rate of success for smoking cessation is greater with the sustained care program. Test the claim using a hypothesis test.

Variation of Hospital Times Use the sample data given in Exercise 7 “Seat Belts” and test the claim that for children hospitalized after motor vehicle crashes, the numbers of days in intensive care units for those wearing seat belts and for those not wearing seat belts have the same variation. Use a 0.05 significance level.

Are Seat Belts Effective? A simple random sample of front-seat occupants involved in car crashes is obtained. Among 2823 occupants not wearing seat belts, 31 were killed. Among 7765 occupants wearing seat belts, 16 were killed (based on data from “Who Wants Airbags?” by Meyer and Finney, Chance, Vol. 18, No. 2). We want to use a 0.05 significance level to test the claim that seat belts are effective in reducing fatalities.

a. Test the claim using a hypothesis test.

Independent Samples Which of the following involve independent samples?

a. Data Set 4 “Measured and Reported” includes measured heights matched with the heights that were reported when the subjects were asked for those values.

Overlap of Confidence Intervals In the article “On Judging the Significance of Differences by Examining the Overlap Between Confidence Intervals,” by Schenker and Gentleman (American Statistician, Vol. 55, No. 3), the authors consider sample data in this statement: “Independent simple random samples, each of size 200, have been drawn, and 112 people in the first sample have the attribute, whereas 88 people in the second sample have the attribute.”

a. Use the methods of this section to construct a 95% confidence interval estimate of the difference p1-p2. What does the result suggest about the equality of p1 and p2

.

In Exercises 5–20, assume that the two samples are independent simple random samples selected from normally distributed populations, and do not assume that the population standard deviations are equal. (Note: Answers in Appendix D include technology answers based on Formula 9-1 along with “Table” answers based on Table A-3 with df equal to the smaller of n1-1 and n2-1)

Better Tips by Giving Candy An experiment was conducted to determine whether giving candy to dining parties resulted in greater tips. The mean tip percentages and standard deviations are given below along with the sample sizes (based on data from “Sweetening the Till: The Use of Candy to Increase Restaurant Tipping,” by Strohmetz et al., Journal of Applied Social Psychology, Vol. 32, No. 2).

a. Use a 0.05 significance level to test the claim that giving candy does result in greater tips.

[Image]

Cigarette Pack Warnings A study was conducted to find the effects of cigarette pack warnings that consisted of text or pictures. Among 1078 smokers given cigarette packs with text warnings, 366 tried to quit smoking. Among 1071 smokers given cigarette packs with warning pictures, 428 tried to quit smoking. (Results are based on data from “Effect of Pictorial Cigarette Pack Warnings on Changes in Smoking Behavior,” by Brewer et al., Journal of the American Medical Association.) Use a 0.01 significance level to test the claim that the proportion of smokers who tried to quit in the text warning group is less than the proportion in the picture warning group.

a. Test the claim using a hypothesis test.

In Exercises 5–16, use the listed paired sample data, and assume that the samples are simple random samples and that the differences have a distribution that is approximately normal.

Heights of Presidents A popular theory is that presidential candidates have an advantage if they are taller than their main opponents. Listed are heights (cm) of presidents along with the heights of their main opponents (from Data Set 22 “Presidents” in Appendix B).

a. Use the sample data with a 0.05 significance level to test the claim that for the population of heights of presidents and their main opponents, the differences have a mean greater than 0 cm.

Can Dogs Detect Malaria? A study was conducted to determine whether dogs could detect malaria from socks worn by malaria patients and socks worn by patients without malaria. Among 175 socks worn by malaria patients, the dogs made correct identifications 123 times. Among 145 socks worn by patients without malaria, the dogs made correct identifications 131 times (based on data presented at an annual meeting of the American Society of Tropical Medicine, by principal investigator Steve Lindsay). Use a 0.05 significance level to test the claim of no difference between the two rates of correct responses.

a. Test the claim using a hypothesis test.

Friday the 13th Refer to the sample data from Exercise 1.

a. Find the differences d, then find the values of d_bar and sd

In Exercises 5–20, assume that the two samples are independent simple random samples selected from normally distributed populations, and do not assume that the population standard deviations are equal. (Note: Answers in Appendix D include technology answers based on Formula 9-1 along with “Table” answers based on Table A-3 with df equal to the smaller of n1-1 and n2-1)

Magnet Treatment of Pain People spend around $5 billion annually for the purchase of magnets used to treat a wide variety of pains. Researchers conducted a study to determine whether magnets are effective in treating back pain. Pain was measured using the visual analog scale, and the results given below are among the results obtained in the study (based on data from “Bipolar Permanent Magnets for the Treatment of Chronic Lower Back Pain: A Pilot Study,” by Collacott, Zimmerman, White, and Rindone, Journal of the American Medical Association, Vol. 283, No. 10). Higher scores correspond to greater pain levels.

a. Use a 0.05 significance level to test the claim that those treated with magnets have a greater mean reduction in pain than those given a sham treatment (similar to a placebo).

Second-Hand Smoke Samples from Data Set 15 “Passive and Active Smoke” include cotinine levels measured in a group of smokers ( n = 40, x_bar = 172.48 ng/mL, 119.50 ng/mL ) and a group of nonsmokers not exposed to tobacco smoke ( n = 40, x_bar = 16.35 ng/mL, 62.53 ng/mL ). Cotinine is a metabolite of nicotine, meaning that when nicotine is absorbed by the body, cotinine is produced.

a. Use a 0.05 significance level to test the claim that the variation of cotinine in smokers is greater than the variation of cotinine in nonsmokers not exposed to tobacco smoke.

In Exercises 5–16, use the listed paired sample data, and assume that the samples are simple random samples and that the differences have a distribution that is approximately normal.

The Freshman 15 The “Freshman 15” refers to the belief that college students gain 15 lb (or 6.8 kg) during their freshman year. Listed below are weights (kg) of randomly selected male college freshmen (from Data Set 13 “Freshman 15” in Appendix B). The weights were measured in September and later in April.

a. Use a 0.01 significance level to test the claim that for the population of freshman male college students, the weights in September are less than the weights in the following April.

In Exercises 5–20, assume that the two samples are independent simple random samples selected from normally distributed populations, and do not assume that the population standard deviations are equal. (Note: Answers in Appendix D include technology answers based on Formula 9-1 along with “Table” answers based on Table A-3 with df equal to the smaller of n1-1 and n2-1)

Color and Cognition Researchers from the University of British Columbia conducted a study to investigate the effects of color on cognitive tasks. Words were displayed on a computer screen with background colors of red and blue. Results from scores on a test of word recall are given below. Higher scores correspond to greater word recall.

a. Use a 0.05 significance level to test the claim that the samples are from populations with the same mean.

Count Five Test for Comparing Variation in Two Populations Repeat Exercise 16 “Blanking Out on Tests,” but instead of using the F test, use the following procedure for the “count five” test of equal variations (which is not as complicated as it might appear).

a. For each value x in the first sample, find the absolute deviation |x-x_bar| then sort the absolute deviation values. Do the same for the second sample.

In Exercises 5–16, use the listed paired sample data, and assume that the samples are simple random samples and that the differences have a distribution that is approximately normal.

Do Men Talk Less than Women? Listed below are word counts of males and females in couple relationships (from Data Set 14 “Word Counts” in Appendix B).

a. Use a 0.05 significance level to test the claim that men talk less than women.

Confidence Interval Assume that we want to use the sample data in Exercise 1 for constructing a confidence interval to be used for testing the given claim.

a. What is the confidence level that should be used for the confidence interval?

In Exercises 5–20, assume that the two samples are independent simple random samples selected from normally distributed populations, and do not assume that the population standard deviations are equal. (Note: Answers in Appendix D include technology answers based on Formula 9-1 along with “Table” answers based on Table A-3 with df equal to the smaller of n1-1 and n2-1)

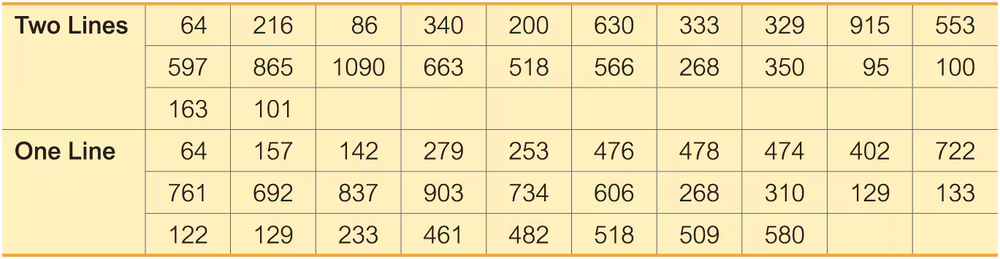
Queues Listed on the next page are waiting times (seconds) of observed cars at a Delaware inspection station. The data from two waiting lines are real observations, and the data from the single waiting line are modeled from those real observations. These data are from Data Set 30 “Queues” in Appendix B. The data were collected by the author.

a. Use a 0.01 significance level to test the claim that cars in two queues have a mean waiting time equal to that of cars in a single queue.

In Exercises 5–20, assume that the two samples are independent simple random samples selected from normally distributed populations, and do not assume that the population standard deviations are equal. (Note: Answers in Appendix D include technology answers based on Formula 9-1 along with “Table” answers based on Table A-3 with df equal to the smaller of n1-1 and n2-1)

Readability of Font On a Computer Screen The statistics shown below were obtained from a standard test of readability of fonts on a computer screen (based on data from “Reading on the Computer Screen: Does Font Type Have Effects on Web Text Readability?” by Ali et al., International Education Studies, Vol. 6, No. 3). Reading speed and accuracy were combined into a readability performance score (x), where a higher score represents better font readability.

a. Use a 0.05 significance level to test the claim that there is no significant difference in readability between Roman and Arial fonts.

In Exercises 5–20, assume that the two samples are independent simple random samples selected from normally distributed populations, and do not assume that the population standard deviations are equal. (Note: Answers in Appendix D include technology answers based on Formula 9-1 along with “Table” answers based on Table A-3 with df equal to the smaller of n1-1 and n2-1)

Bicycle Commuting A researcher used two different bicycles to commute to work. One bicycle was steel and weighed 30.0 lb; the other was carbon and weighed 20.9 lb. The commuting times (minutes) were recorded with the results shown below (based on data from “Bicycle Weights and Commuting Time,” by Jeremy Groves, British Medical Journal).

a. Use a 0.05 significance level to test the claim that the mean commuting time with the heavier bicycle is the same as the mean commuting time with the lighter bicycle.

Pulse Rates of Women and Men Using the samples of women and men included in Data Set 1 “Body Data,” we get this 95% confidence interval estimate of the difference between the population mean of pulse rates (bpm) of women and the population mean of pulse rates (bpm) of men: 1.7 bpm < u1-u2 < 7.2bpm. In this confidence interval, women correspond to population 1 and men correspond to population 2.

a. What does the confidence interval suggest about equality of the mean pulse rate of women and the mean pulse rate of men?

F Test Statistic

a. If s2,1 represents the larger of two sample variances, can the F test statistic ever be less than 1?

In Exercises 5–16, use the listed paired sample data, and assume that the samples are simple random samples and that the differences have a distribution that is approximately normal.

Measured and Reported Weights Listed below are measured and reported weights (lb) of random female subjects (from Data Set 4 “Measured and Reported” in Appendix B).

a. Use a 0.05 significance level to test the claim that for females, the measured weights tend to be higher than the reported weights.

In Exercises 5–20, assume that the two samples are independent simple random samples selected from normally distributed populations, and do not assume that the population standard deviations are equal. (Note: Answers in Appendix D include technology answers based on Formula 9-1 along with “Table” answers based on Table A-3 with df equal to the smaller of n1-1 and n2-1)

Color and Creativity Researchers from the University of British Columbia conducted trials to investigate the effects of color on creativity. Subjects with a red background were asked to think of creative uses for a brick; other subjects with a blue background were given the same task. Responses were scored by a panel of judges and results from scores of creativity are given below. Higher scores correspond to more creativity. The researchers make the claim that “blue enhances performance on a creative task.”

a. Use a 0.01 significance level to test the claim that blue enhances performance on a creative task.

Hypotheses and Conclusions Refer to the hypothesis test described in Exercise 1.

a. Identify the null hypothesis and the alternative hypothesis.

Second-Hand Smoke Samples from Data Set 15 “Passive and Active Smoke” include cotinine levels measured in a group of smokers ( n = 40, x_bar = 172.48 ng/mL, 119.50 ng/mL ) and a group of nonsmokers not exposed to tobacco smoke ( n = 40, x_bar = 16.35 ng/mL, 62.53 ng/mL ). Cotinine is a metabolite of nicotine, meaning that when nicotine is absorbed by the body, cotinine is produced.

b. The 40 cotinine measurements from the nonsmoking group consist of these values (all in ng/mL): 1, 1, 90, 244, 309, and 35 other values that are all 0. Does this sample appear to be from a normally distributed population? If not, how are the results from part (a) affected?

F Test Statistic

b. Can the F test statistic ever be a negative number?

In Exercises 5–20, assume that the two samples are independent simple random samples selected from normally distributed populations, and do not assume that the population standard deviations are equal. (Note: Answers in Appendix D include technology answers based on Formula 9-1 along with “Table” answers based on Table A-3 with df equal to the smaller of n1-1 and n2-1)

Color and Cognition Researchers from the University of British Columbia conducted a study to investigate the effects of color on cognitive tasks. Words were displayed on a computer screen with background colors of red and blue. Results from scores on a test of word recall are given below. Higher scores correspond to greater word recall.

b. Construct a confidence interval appropriate for the hypothesis test in part (a). What is it about the confidence interval that causes us to reach the same conclusion from part (a)?

Count Five Test for Comparing Variation in Two Populations Repeat Exercise 16 “Blanking Out on Tests,” but instead of using the F test, use the following procedure for the “count five” test of equal variations (which is not as complicated as it might appear).

b. Let c1 be the count of the number of absolute deviation values in the first sample that are greater than the largest absolute deviation value in the other sample. Also, let C2 be the count of the number of absolute deviation values in the second sample that are greater than the largest absolute deviation value in the other sample. (One of these counts will always be zero.)

In Exercises 5–16, use the listed paired sample data, and assume that the samples are simple random samples and that the differences have a distribution that is approximately normal.

The Freshman 15 The “Freshman 15” refers to the belief that college students gain 15 lb (or 6.8 kg) during their freshman year. Listed below are weights (kg) of randomly selected male college freshmen (from Data Set 13 “Freshman 15” in Appendix B). The weights were measured in September and later in April.

b. Construct the confidence interval that could be used for the hypothesis test described in part (a). What feature of the confidence interval leads to the same conclusion reached in part (a)?