Back
BackProblem 2.T.9
Use the frequency distribution in Exercise 4 to estimate the sample mean and sample standard deviation of the data. Do the formulas for grouped data give results that are as accurate as the individual entry formulas? Explain.
Problem 2.CR.6b
The mean annual salary for a sample of electrical engineers is $86,500, with a standard deviation of $1500. The data set has a bell-shaped distribution.
b. The salaries of three randomly selected electrical engineers are $93,500, $85,600, and $82,750. Find the z-score that corresponds to each salary. Determine whether any of these salaries are unusual.
Problem 2.R.46
The towing capacities (in pounds) of all the pickup trucks at a dealership have a bell-shaped distribution, with a mean of 11,830 pounds and a standard deviation of 2370 pounds. In Exercises 45– 48, use the corresponding z-score to determine whether the towing capacity is unusual. Explain your reasoning.
5,500 pounds
Problem 2.T.8b
The mean gestational length of a sample of 208 horses is 343.7 days, with a standard deviation of 10.4 days. The data set has a bell-shaped distribution.
b. Determine whether a gestational length of 318.4 days is unusual.
Problem 2.Q.1d
The data set represents the number of minutes a sample of 27 people exercise each week.
108 139 120 123 120 132 123 131 131
157 150 124 111 101 135 119 116 117
127 128 139 119 118 114 127 142 130
d. Describe the shape of the distribution as symmetric, uniform, skewed left, skewed right, or none of these.
Problem 2.R.22
In Exercises 21 and 22, determine whether the approximate shape of the distribution in the histogram is symmetric, uniform, skewed left, skewed right, or none of these.
Problem 2.R.19
Describe the shape of the distribution for the histogram you made in Exercise 3 as symmetric, uniform, skewed left, skewed right, or none of these.
Problem 2.T.5
"According to data from the city of Toronto, Ontario, Canada, there were nearly 112,000 parking infractions in the city for December 2020, with fines totaling over 5,500,000 Canadian dollars. The fines (in Canadian dollars) for a random sample of 105 parking infractions in Toronto, Ontario, Canada, for December 2020 are listed below. (Source: City of Toronto)
In Exercises 1–5, use technology. If possible, print your results.
Draw a histogram for the data. Does the distribution appear to be bell-shaped?"
Problem 2.1.45b
What Would You Do? You work at a bank and are asked to recommend the amount of cash to put in an ATM each day. You do not want to put in too much (which would cause security concerns) or too little (which may create customer irritation). The daily withdrawals (in hundreds of dollars) for 30 days are listed. 72 84 61 76 104 76 86 92 80 88 98 76 97 82 84 67 70 81 82 89 74 73 86 81 85 78 82 80 91 83
If you put $9000 in the ATM each day, what percent of the days in a month should you expect to run out of cash? Explain.
Problem 2.1.45c
What Would You Do? You work at a bank and are asked to recommend the amount of cash to put in an ATM each day. You do not want to put in too much (which would cause security concerns) or too little (which may create customer irritation). The daily withdrawals (in hundreds of dollars) for 30 days are listed. 72 84 61 76 104 76 86 92 80 88 98 76 97 82 84 67 70 81 82 89 74 73 86 81 85 78 82 80 91 83
If you are willing to run out of cash on 10% of the days, how much cash should you put in the ATM each day? Explain.
Problem 2.1.46c
What Would You Do? The admissions department for a college is asked to recommend the minimum SAT scores that the college will accept for full-time students. The SAT scores of 50 applicants are listed. 1170 1000 910 870 1070 1290 920 1470 1080 1180 770 900 1120 1070 1370 1160 970 930 1240 1270 1250 1330 1010 1010 1410 1130 1210 1240 960 820 650 1010 1190 1500 1400 1270 1310 1050 950 1150 1450 1290 1310 1100 1330 1410 840 1040 1090 1080
If you want to accept the top 88% of the applicants, what should the minimum score be? Explain.
Problem 2.1.3
What is the difference between class limits and class boundaries?
Problem 2.1.6
What is the difference between a frequency polygon and an ogive?
Problem 2.1.13
use the given information about the data set and the number of classes to find the class width, the lower class limits, and the upper class limits.
min=17, range=118, 8 classes
Problem 2.1.16
use the frequency distribution to find the (a) class width, (b) class midpoints, and (c) class boundaries.
Toledo, OH, Average Normal Temperatures (F)
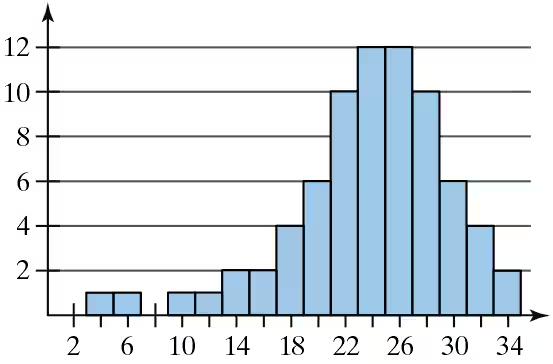
Problem 2.1.26a
use the ogive to approximate
the number in the sample.
Problem 2.1.27c
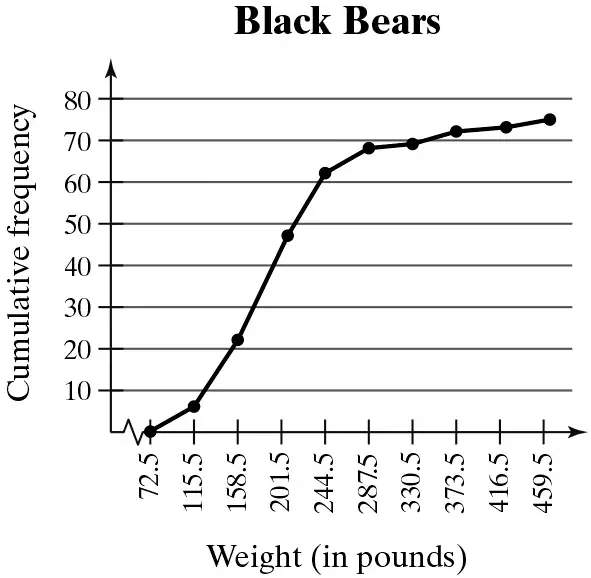
Use the ogive to approximate the
the number of black bears that weigh between 158.5 pounds and 244.5 pounds.
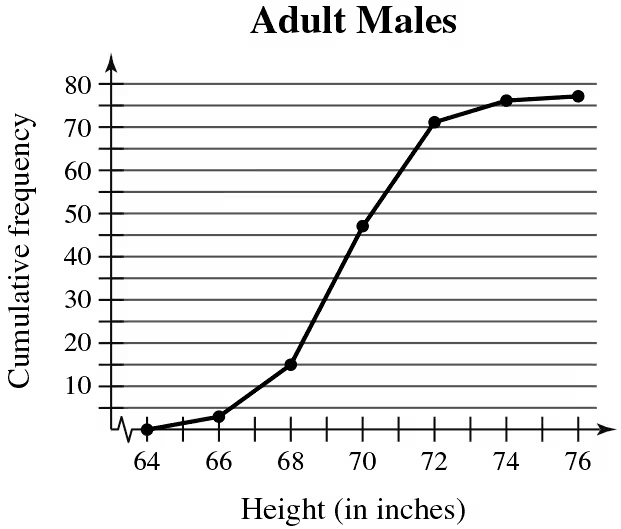
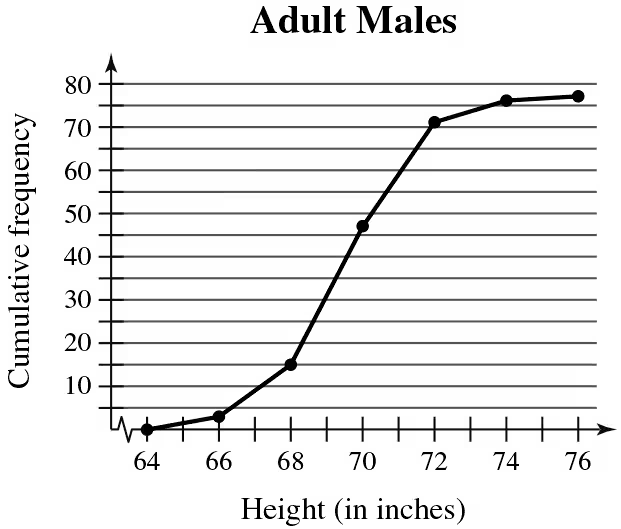
Problem 2.1.28b
Use the ogive to approximate
the height for which the cumulative frequency is 15.
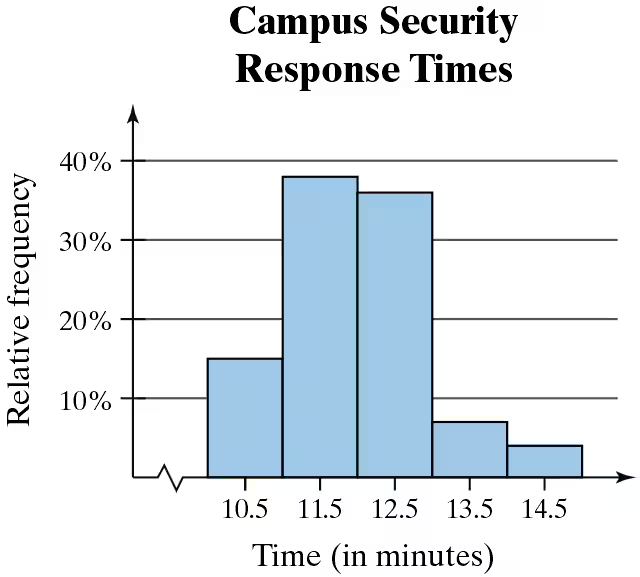
Problem 2.1.24c
Use the relative frequency histogram to describe any patterns with the data.
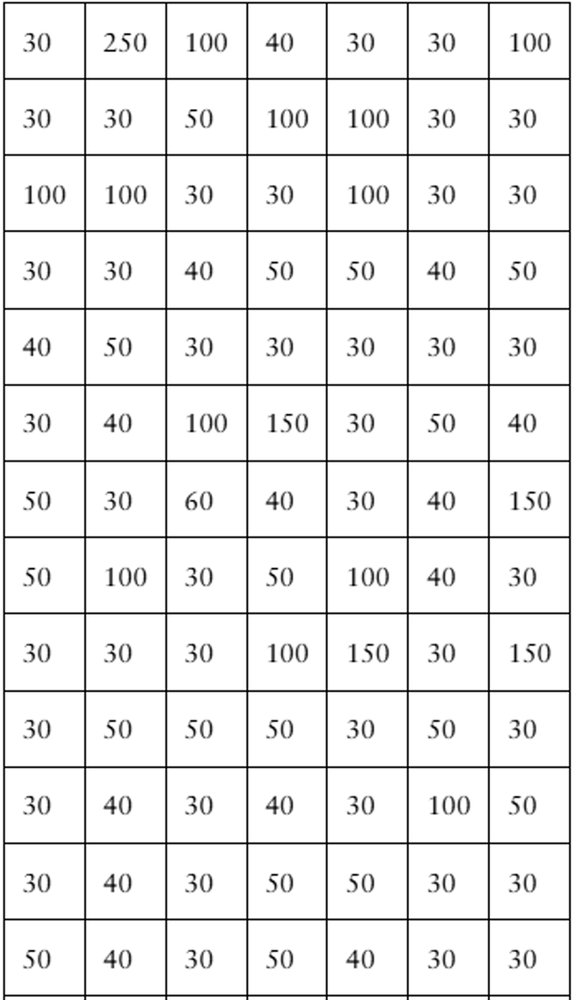
Problem 2.1.37
Constructing a Frequency Distribution and a Relative Frequency Histogram In Exercises 37–40, construct a frequency distribution and a relative frequency histogram for the data set using five classes. Which class has the greatest relative frequency and which has the least relative frequency?
Taste Test
Data set: Ratings from 1 (lowest) to 10 (highest) provided by 36 people after taste-testing a new flavor of protein bar 2 6 9 2 9 9 6 10 5 8 7 6 5 10 1 4 9 3 4 5 3 6 5 2 4 9 2 9 3 3 6 5 1 9 4 2
Problem 2.1.41
Construct a cumulative frequency distribution and an ogive for the data set using six classes. Then describe the location of the greatest increase in frequency.
Retirement Ages
Data set: Retirement ages of 35 English professors 72 62 55 61 53 62 65 66 69 55 66 63 67 69 55 65 67 57 67 68 73 75 65 54 71 57 52 58 58 71 72 67 63 65 61
Problem 2.1.45a
What Would You Do? You work at a bank and are asked to recommend the amount of cash to put in an ATM each day. You do not want to put in too much (which would cause security concerns) or too little (which may create customer irritation). The daily withdrawals (in hundreds of dollars) for 30 days are listed. 72 84 61 76 104 76 86 92 80 88 98 76 97 82 84 67 70 81 82 89 74 73 86 81 85 78 82 80 91 83
Construct a relative frequency histogram for the data. Use 8 classes.
Problem 2.1.30
Construct a frequency distribution for the data set using the indicated number of classes. In the table, include the midpoints, relative frequencies, and cumulative frequencies. Which class has the greatest class frequency and which has the least class frequency.
Textbook Spending
Number of classes: 6
Data set: Amounts (in dollars) spent on textbooks for a semester 91 472 279 249 530 376 188 341 266 199 142 273 189 130 489 266 248 101 375 486 190 398 188 269 43 30 127 354 84 319
Problem 2.1.33
Construct a frequency distribution and a frequency histogram for the data set using the indicated number of classes. Describe any patterns.
Reaction Times
Number of classes: 8
Data set: Reaction times (in milliseconds) of 30 adult females to an auditory stimulus 507 389 305 291 336 310 514 442 373 428 387 454 323 441 388 426 411 382 320 450 309 416 359 388 307 337 469 351 422 413
Problem 2.1.10
Determine whether the statement is true or false. If it is false, rewrite it as a true statement.
Class boundaries ensure that consecutive bars of a histogram touch.
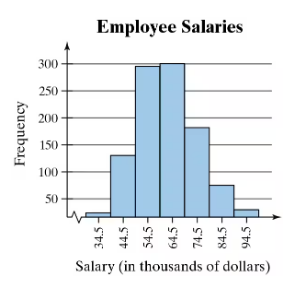
Problem 2.1.19a
Use the frequency histogram
a. to determine the number of classes.
Problem 2.1.19d
Use the frequency histogram
d. describe any patterns with the data..
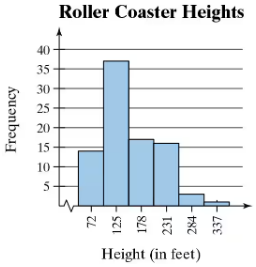
Problem 2.1.20d
Use the frequency histogram
describe any patterns with the data..
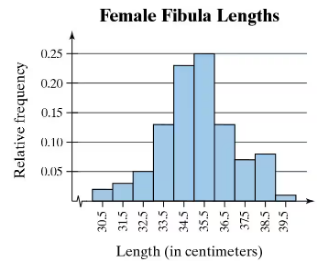
Problem 2.1.23b
Use the relative frequency histogram to
approximate the greatest and least relative frequencies.
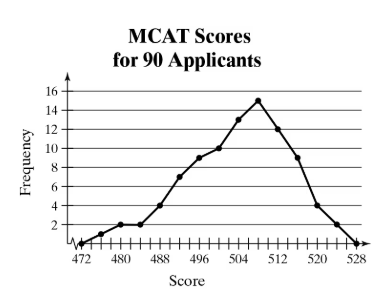
Problem 2.1.21
use the frequency polygon to identify the class with the greatest, and the class with the least, frequency.