Table of contents

1. Intro to Stats and Collecting Data55m
2. Describing Data with Tables and Graphs1h 55m
3. Describing Data Numerically1h 45m
4. Probability2h 16m
5. Binomial Distribution & Discrete Random Variables2h 33m
6. Normal Distribution and Continuous Random Variables1h 38m
7. Sampling Distributions & Confidence Intervals: Mean1h 53m
8. Sampling Distributions & Confidence Intervals: Proportion1h 12m
- Sampling Distribution of Sample Proportion
  29m
- Confidence Intervals for Population Proportion
  42m
9. Hypothesis Testing for One Sample2h 19m
10. Hypothesis Testing for Two Samples3h 22m
11. Correlation1h 6m
12. Regression1h 4m
13. Chi-Square Tests & Goodness of Fit1h 20m
14. ANOVA1h 0m

2. Describing Data with Tables and Graphs

Frequency Distributions

Statistics

2. Describing Data with Tables and Graphs

Frequency Distributions

Previous problemNext problem

1:14 minutes

Problem 2.1.26a

Textbook Question

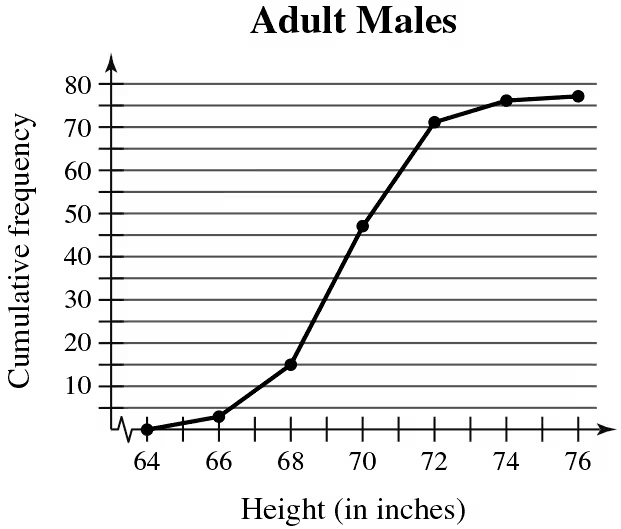
use the ogive to approximate
the number in the sample.

Verified step by step guidance

Step 1: Understand the ogive graph. An ogive is a cumulative frequency graph that shows the total number of observations below a certain value. In this case, the graph represents the cumulative frequency of adult males' heights in inches.

Step 2: Identify the highest cumulative frequency on the graph. The highest point on the ogive corresponds to the total number of observations in the sample. In this graph, the cumulative frequency reaches 80 at the height of 76 inches.

Step 3: Approximate the total sample size. Since the cumulative frequency at the highest point represents the total number of individuals in the sample, the total sample size is approximately 80.

Step 4: Verify the interpretation. Ensure that the cumulative frequency values increase consistently and that the graph ends at the total sample size. This confirms the ogive is correctly interpreted.

Step 5: Use the ogive for further analysis. You can use the graph to determine the number of individuals below specific height thresholds or calculate proportions within certain ranges.

Verified video answer for a similar problem:

This video solution was recommended by our tutors as helpful for the problem above

Video duration:

Play a video:

Was this helpful?

Key Concepts

Here are the essential concepts you must grasp in order to answer the question correctly.

Ogive

An ogive is a graphical representation of cumulative frequency, which shows the number of observations that fall below a particular value in a dataset. It is constructed by plotting cumulative frequencies against the upper boundaries of the class intervals. The resulting curve helps in understanding the distribution of data and can be used to estimate the number of observations within specific ranges.

Cumulative Frequency

Cumulative frequency is the running total of frequencies in a dataset, which indicates how many observations fall below or at a certain value. It is calculated by adding the frequency of each class interval to the sum of the frequencies of all preceding intervals. This concept is essential for constructing ogives and helps in analyzing the distribution of data over a range.

Interpreting Graphs

Interpreting graphs involves analyzing visual data representations to extract meaningful information. In the context of an ogive, one must understand how to read the axes, identify key points, and determine cumulative frequencies at specific heights. This skill is crucial for making approximations and drawing conclusions based on the graphical data presented.

Watch next

Master Intro to Frequency Distributions with a bite sized video explanation from Patrick

Start learning

Related Videos

Related Practice

Textbook Question

Hershey Kisses Refer to Data Set 38 “Candies” and use the weights (grams) of Hershey’s Kisses. Begin with a lower class limit of 4.300 g and use a class width of 0.100 g. Does this distribution appear to be a normal distribution?

Textbook Question

Testing Goodness-of-Fit with a Normal Distribution Refer to Data Set 1 “Body Data” in Appendix B for the heights of females.

" style="" width="600">

a. Enter the observed frequencies in the table above.

Textbook Question

What is the difference between a frequency polygon and an ogive?

Textbook Question

use the frequency distribution to find the (a) class width, (b) class midpoints, and (c) class boundaries.

Toledo, OH, Average Normal Temperatures (F)

Textbook Question

Use the ogive to approximate

the height for which the cumulative frequency is 15.

Textbook Question

Use the ogive to approximate the

the number of black bears that weigh between 158.5 pounds and 244.5 pounds.

Textbook Question

In Exercises 17–19, use the data set, which represents the points recorded by each player on the Winnipeg Jets in the 2019–2020 NHL season. (Source: National Hockey League)

8 8 8 6 0 73 26 1

0 5 58 1 7 5 10 63

0 5 10 0 31 5 15 45

16 29 10 73 5 3 0 65

Construct a frequency distribution for the data set using eight classes. Include class limits, midpoints, boundaries, frequencies, relative frequencies, and cumulative frequencies.

Textbook Question

Construct a frequency distribution for the data set using the indicated number of classes. In the table, include the midpoints, relative frequencies, and cumulative frequencies. Which class has the greatest class frequency and which has the least class frequency.

Textbook Spending

Number of classes: 6

Data set: Amounts (in dollars) spent on textbooks for a semester 91 472 279 249 530 376 188 341 266 199 142 273 189 130 489 266 248 101 375 486 190 398 188 269 43 30 127 354 84 319

Show more practices

Download the Mobile app

Privacy

Do not sell my personal information

Accessibility

Patent notice

Sitemap

use the ogive to approximatethe number in the sample.

Key Concepts

Ogive

Cumulative Frequency

Interpreting Graphs

Watch next

use the ogive to approximate
the number in the sample.