Using Probabilities for Significant Events

c. Which probability is relevant for determining whether 1 is a significantly low number of matches: the result from part (a) or part (b)?

Using Probabilities for Significant Events

d. Is 1 a significantly low number of matches? Why or why not?

Biometric Security In a USA Today survey of 510 people, 270 (or 53%) said that we should replace passwords with biometric security, such as fingerprints. Use the following probabilities related to determining whether the result of 270 is significantly high (assuming the true rate is 50%). Is 270 significantly high? What should be concluded about the claim that the majority of the population says that we should replace passwords with biometric security? Explain.

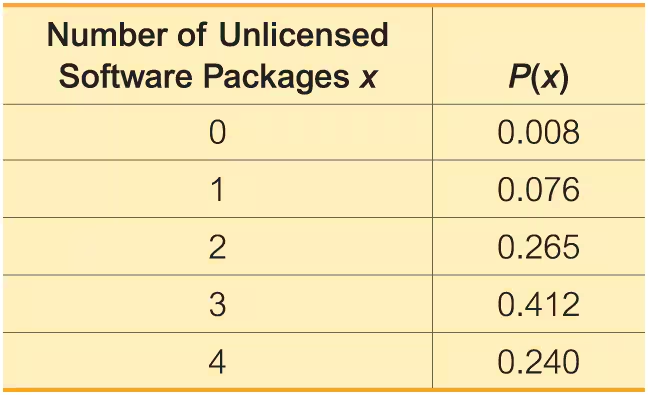
Random Variable The accompanying table lists probabilities for the corresponding numbers of unlicensed software packages when four software packages are randomly selected in China. What is the random variable, what are its possible values, and are its values numerical?

Identifying Discrete and Continuous Random Variables. In Exercises 5 and 6, refer to the given values, then identify which of the following is most appropriate: discrete random variable, continuous random variable, or not a random variable.

a. IQ scores of statistics students

b. Exact heights of statistics students

c. Shoe sizes (such as 8 or 8½) of statistics students

d. Majors (such as history) of statistics students

e. The number of rolls of a die required for a statistics student to get the number 4

Stem Cell Survey In a Newsweek poll of 882 adults, 481 (or 55%) said that they were in favor of using federal tax money to fund medical research using stem cells obtained from human embryos. A politician claims that people don’t really understand the stem cell issue and their responses to such questions are random responses equivalent to a coin toss. Use the following probabilities related to determining whether the result of 481 is significantly high (assuming the true rate is 50%). Is 481 significantly high? What should be concluded about the politician’s claim? Explain.

P(respondent says to use the federal tax money) = 0.5

P(among 882, exactly 481 says to use federal tax money) = 0.000713

P(among 882,481 or more say to use federal tax money) = 0.00389

Expected Value for the Florida Pick 3 Lottery In the Florida Pick 3 lottery, you can bet $1 by selecting three digits, each between 0 and 9 inclusive. If the same three numbers are drawn in the same order, you win and collect $500.

d. Find the expected value for a $1 bet.

Expected Value in North Carolina’s Pick 4 Game In North Carolina’s Pick 4 lottery game, you can pay $1 to select a four-digit number from 0000 through 9999. If you select the same sequence of four digits that are drawn, you win and collect $5000.

d. Find the expected value.

Expected Value in North Carolina’s Pick 4 Game In North Carolina’s Pick 4 lottery game, you can pay $1 to select a four-digit number from 0000 through 9999. If you select the same sequence of four digits that are drawn, you win and collect $5000.

e. If you bet $1 in North Carolina’s Pick 3 game, the expected value is Which bet is better in the sense of a producing a higher expected value: A $1 bet in the North Carolina Pick 4 game or a $1 bet in the North Carolina Pick 3 game?

Discrete or Continuous? Is the random variable given in the table from Exercise 1 discrete or continuous? Explain.

Identifying Probability Distributions. In Exercises 7–14, determine whether a probability distribution is given. If a probability distribution is given, find its mean and standard deviation. If a probability distribution is not given, identify the requirements that are not satisfied.

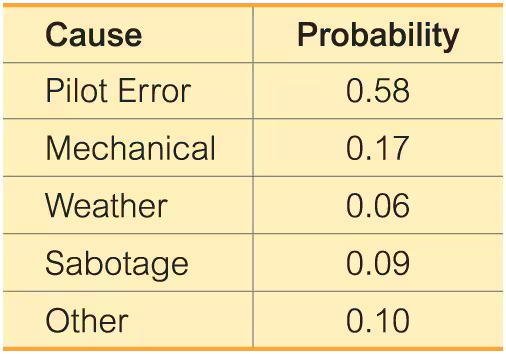
Plane Crashes The table lists causes of fatal plane crashes with their corresponding probabilities.

Identifying Probability Distributions. In Exercises 7–14, determine whether a probability distribution is given. If a probability distribution is given, find its mean and standard deviation. If a probability distribution is not given, identify the requirements that are not satisfied.

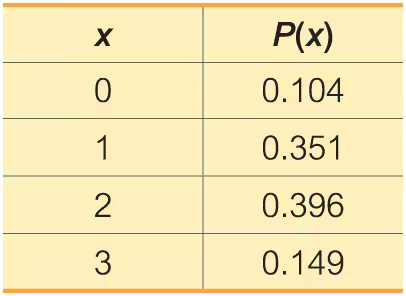
Online Courses College students are randomly selected and arranged in groups of three. The random variable x is the number in the group who say that they take one or more online courses (based on data from Sallie Mae).

Identifying Probability Distributions. In Exercises 7–14, determine whether a probability distribution is given. If a probability distribution is given, find its mean and standard deviation. If a probability distribution is not given, identify the requirements that are not satisfied.

Fear of Heights The table lists results from a survey of 285 subjects who were asked, “Are you afraid of heights in tall buildings?” The results are from USA Today.

Binomial Probability Formula. In Exercises 13 and 14, answer the questions designed to help understand the rationale for the binomial probability formula.

Guessing Answers Standard tests, such as the SAT, ACT, or Medical College Admission Test (MCAT), typically use multiple choice questions, each with five possible answers (a, b, c, d, e), one of which is correct. Assume that you guess the answers to the first three questions.

b. Beginning with WWC, make a complete list of the different possible arrangements of two wrong answers and one correct answer, and then find the probability for each entry in the list.

Binomial Probability Formula. In Exercises 13 and 14, answer the questions designed to help understand the rationale for the binomial probability formula.

Guessing Answers Standard tests, such as the SAT, ACT, or Medical College Admission Test (MCAT), typically use multiple choice questions, each with five possible answers (a, b, c, d, e), one of which is correct. Assume that you guess the answers to the first three questions.

c. Based on the preceding results, what is the probability of getting exactly one correct answer when three guesses are made?

40% of consumers believe that cash will be obsolete in the next 20 years (based on a survey by J.P. Morgan Chase). In each of Exercises 15–20, assume that 8 consumers are randomly selected. Find the indicated probability.

Find the probability that exactly 6 of the selected consumers believe that cash will be obsolete in the next 20 years.

40% of consumers believe that cash will be obsolete in the next 20 years (based on a survey by J.P. Morgan Chase). In each of Exercises 15–20, assume that 8 consumers are randomly selected. Find the indicated probability.

Find the probability that at least 6 of the selected consumers believe that cash will be obsolete in the next 20 years.

40% of consumers believe that cash will be obsolete in the next 20 years (based on a survey by J.P. Morgan Chase). In each of Exercises 15–20, assume that 8 consumers are randomly selected. Find the indicated probability.

Find the probability that fewer than 3 of the selected consumers believe that cash will be obsolete in the next 20 years.

40% of consumers believe that cash will be obsolete in the next 20 years (based on a survey by J.P. Morgan Chase). In each of Exercises 15–20, assume that 8 consumers are randomly selected. Find the indicated probability.

Find the probability that no more than 3 of the selected consumers believe that cash will be obsolete in the next 20 years.

In Exercises 25–28, find the probabilities and answer the questions.

Whitus v. Georgia In the classic legal case of Whitus v. Georgia, a jury pool of 90 people was supposed to be randomly selected from a population in which 27% were minorities. Among the 90 people selected, 7 were minorities. Find the probability of getting 7 or fewer minorities if the jury pool was randomly selected. Is the result of 7 minorities significantly low? What does the result suggest about the jury selection process?

Politics The County Clerk in Essex, New Jersey, was accused of cheating by not using randomness in assigning the order in which candidates’ names appeared on voting ballots. Among 41 different ballots, Democrats were assigned the desirable first line 40 times. Assume that Democrats and Republicans are assigned the first line using a method of random selection so that they are equally likely to get that first line.

.

d. Which probability is relevant for determining whether 40 first lines for Democrats is significantly high: the probability from part (b) or part (c)? Based on the relevant probability, is the result of 40 first lines for Democrats significantly high?

Politics The County Clerk in Essex, New Jersey, was accused of cheating by not using randomness in assigning the order in which candidates’ names appeared on voting ballots. Among 41 different ballots, Democrats were assigned the desirable first line 40 times. Assume that Democrats and Republicans are assigned the first line using a method of random selection so that they are equally likely to get that first line.

e. What do the results suggest about how the clerk met the requirement of using a random method to assign the order of candidates’ names on voting ballots?

One of Mendel’s famous experiments with peas resulted in 580 offspring, and 152 of them were yellow peas. Mendel claimed that under the same conditions, 25% of offspring peas would be yellow. Assume that Mendel’s claim of 25% is true, and assume that a sample consists of 580 offspring peas.

a. Use the range rule of thumb to identify the limits separating values that are significantly low and those that are significantly high. Based on the results, is the result of 152 yellow peas either significantly low or significantly high?

One of Mendel’s famous experiments with peas resulted in 580 offspring, and 152 of them were yellow peas. Mendel claimed that under the same conditions, 25% of offspring peas would be yellow. Assume that Mendel’s claim of 25% is true, and assume that a sample consists of 580 offspring peas.

b. Find the probability of exactly 152 yellow peas.

One of Mendel’s famous experiments with peas resulted in 580 offspring, and 152 of them were yellow peas. Mendel claimed that under the same conditions, 25% of offspring peas would be yellow. Assume that Mendel’s claim of 25% is true, and assume that a sample consists of 580 offspring peas.

c. Find the probability of 152 or more yellow peas.

In Exercises 25–28, find the probabilities and answer the questions.

Internet Voting Based on a Consumer Reports survey, 39% of likely voters would be willing to vote by Internet instead of the in-person traditional method of voting. For each of the following, assume that 15 likely voters are randomly selected.

a. What is the probability that exactly 12 of those selected would do Internet voting?

In Exercises 29 and 30, assume that different groups of couples use the XSORT method of gender selection and each couple gives birth to one baby. The XSORT method is designed to increase the likelihood that a baby will be a girl, but assume that the method has no effect, so the probability of a girl is 0.5.

Gender Selection Assume that the groups consist of 36 couples.

b. Use the range rule of thumb to find the values separating results that are significantly low or significantly high.

In Exercises 31 and 32, assume that hybridization experiments are conducted with peas having the property that for offspring, there is a 0.75 probability that a pea has green pods (as in one of Mendel’s famous experiments).

Hybrids Assume that offspring peas are randomly selected in groups of 16.

a. Find the mean and standard deviation for the numbers of peas with green pods in the groups of 16.

In Exercises 31 and 32, assume that hybridization experiments are conducted with peas having the property that for offspring, there is a 0.75 probability that a pea has green pods (as in one of Mendel’s famous experiments).

Hybrids Assume that offspring peas are randomly selected in groups of 16.

b. Use the range rule of thumb to find the values separating results that are significantly low or significantly high.

In Exercises 31 and 32, assume that hybridization experiments are conducted with peas having the property that for offspring, there is a 0.75 probability that a pea has green pods (as in one of Mendel’s famous experiments).

Hybrids Assume that offspring peas are randomly selected in groups of 16.

c. Is a result of 7 peas with green pods a result that is significantly low? Why or why not?