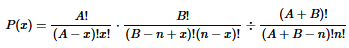In Exercises 29 and 30, assume that different groups of couples use the XSORT method of gender selection and each couple gives birth to one baby. The XSORT method is designed to increase the likelihood that a baby will be a girl, but assume that the method has no effect, so the probability of a girl is 0.5.

Gender Selection Assume that the groups consist of 36 couples.

c. Is the result of 26 girls a result that is significantly high? What does it suggest about the effectiveness of the XSORT method?

Politics The County Clerk in Essex, New Jersey, was accused of cheating by not using randomness in assigning the order in which candidates’ names appeared on voting ballots. Among 41 different ballots, Democrats were assigned the desirable first line 40 times. Assume that Democrats and Republicans are assigned the first line using a method of random selection so that they are equally likely to get that first line.

a. Use the range rule of thumb to identify the limits separating values that are significantly low and those that are significantly high. Based on the results, is the result of 40 first lines for Democrats significantly high?

Politics The County Clerk in Essex, New Jersey, was accused of cheating by not using randomness in assigning the order in which candidates’ names appeared on voting ballots. Among 41 different ballots, Democrats were assigned the desirable first line 40 times. Assume that Democrats and Republicans are assigned the first line using a method of random selection so that they are equally likely to get that first line.

b. Find the probability of exactly 40 first lines for Democrats.

Politics The County Clerk in Essex, New Jersey, was accused of cheating by not using randomness in assigning the order in which candidates’ names appeared on voting ballots. Among 41 different ballots, Democrats were assigned the desirable first line 40 times. Assume that Democrats and Republicans are assigned the first line using a method of random selection so that they are equally likely to get that first line.

c. Find the probability of 40 or more first lines for Democrats.

In Exercises 5–8, assume that the Poisson distribution applies; assume that the mean number of Atlantic hurricanes in the United States is 5.5 per year, as in Example 1; and proceed to find the indicated probability.

a. Find the probability that in a year, there will be no hurricanes.

In Exercises 5–8, assume that the Poisson distribution applies; assume that the mean number of Atlantic hurricanes in the United States is 5.5 per year, as in Example 1; and proceed to find the indicated probability.

b. In a 118-year period, how many years are expected to have no hurricanes?

In Exercises 5–8, assume that the Poisson distribution applies; assume that the mean number of Atlantic hurricanes in the United States is 5.5 per year, as in Example 1; and proceed to find the indicated probability.

a. Find the probability that in a year, there will be 10 hurricanes.

In Exercises 5–8, assume that the Poisson distribution applies; assume that the mean number of Atlantic hurricanes in the United States is 5.5 per year, as in Example 1; and proceed to find the indicated probability.

b. In a 118-year period, how many years are expected to have 10 hurricanes?

In Exercises 9–16, use the Poisson distribution to find the indicated probabilities.

Births In a recent year (365 days), NYU-Langone Medical Center had 5942 births.

a. Find the mean number of births per day.

In Exercises 9–16, use the Poisson distribution to find the indicated probabilities.

Births In a recent year (365 days), NYU-Langone Medical Center had 5942 births.

b. Find the probability that in a single day, there are 16 births.

In Exercises 9–16, use the Poisson distribution to find the indicated probabilities.

Births In a recent year (365 days), NYU-Langone Medical Center had 5942 births.

c. Find the probability that in a single day, there are no births. Would 0 births in a single day be a significantly low number of births?

 In Exercises 5–8, assume that the Poisson distribution applies; assume that the mean number of Atlantic hurricanes in the United States is 5.5 per year, as in Example 1; and proceed to find the indicated probability.

Hurricanes

a. Find the probability that in a year, there will be no hurricanes.

 In Exercises 5–8, assume that the Poisson distribution applies; assume that the mean number of Atlantic hurricanes in the United States is 5.5 per year, as in Example 1; and proceed to find the indicated probability.

Hurricanes

b. In a 118-year period, how many years are expected to have no hurricanes?

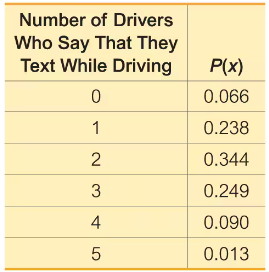
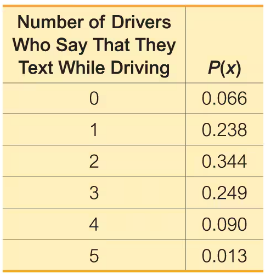
Texting and Driving. In Exercises 21–26, refer to the accompanying table, which describes probabilities for groups of five drivers. The random variable x is the number of drivers in a group who say that they text while driving (based on data from an Arity survey of drivers).

For groups of five drivers, find the mean and standard deviation for the numbers of drivers who say that they text while driving.

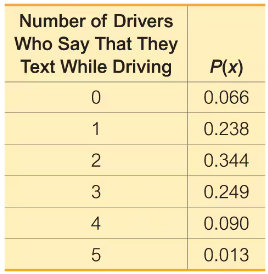
Texting and Driving. In Exercises 21–26, refer to the accompanying table, which describes probabilities for groups of five drivers. The random variable x is the number of drivers in a group who say that they text while driving (based on data from an Arity survey of drivers).

Range Rule of Thumb for Significant Events

Use the range rule of thumb to determine whether 1 is a significantly low number of drivers who say that they text while driving.

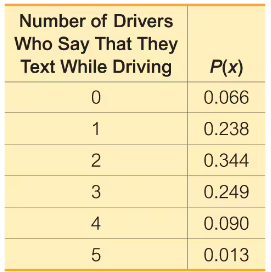
Texting and Driving. In Exercises 21–26, refer to the accompanying table, which describes probabilities for groups of five drivers. The random variable x is the number of drivers in a group who say that they text while driving (based on data from an Arity survey of drivers).

Using Probabilities for Significant Events

b. Find the probability of getting 3 or more drivers who say that they text while driving.

Texting and Driving. In Exercises 21–26, refer to the accompanying table, which describes probabilities for groups of five drivers. The random variable x is the number of drivers in a group who say that they text while driving (based on data from an Arity survey of drivers).

Using Probabilities for Significant Events

d. Is 3 a significantly high number of drivers who say that they text while driving? Why or why not?