Multiple Choice
A student is analyzing different types of variables in a statistics class. Which of the following below is a discrete random variable?
5. Binomial Distribution & Discrete Random Variables
Discrete Random Variables
2:58 minutesProblem 5.1.2
Textbook Question
Discrete or Continuous? Is the random variable given in the table from Exercise 1 discrete or continuous? Explain.
Verified step by step guidance1
Understand the definitions: A discrete random variable takes on a countable number of distinct values (e.g., integers, finite or countably infinite), while a continuous random variable can take on any value within a given range or interval (e.g., real numbers).
Examine the random variable provided in Exercise 1. Determine whether the values it can take are countable (e.g., 0, 1, 2, ...) or if they can take on any value within a range (e.g., 1.5, 2.3, etc.).
If the random variable represents something like the number of occurrences of an event (e.g., number of cars, number of students), it is likely discrete. If it represents measurements (e.g., height, weight, time), it is likely continuous.
Check whether the random variable is described in terms of intervals or specific points. Discrete variables are often associated with specific points, while continuous variables are associated with ranges or intervals.
Based on the analysis, classify the random variable as either discrete or continuous and provide a brief explanation of why it fits that classification.
Verified video answer for a similar problem:This video solution was recommended by our tutors as helpful for the problem above
Video duration:
2mWas this helpful?
Key Concepts
Here are the essential concepts you must grasp in order to answer the question correctly.
Discrete Random Variables
Discrete random variables are those that can take on a countable number of distinct values. Examples include the number of students in a classroom or the outcome of rolling a die. These variables often arise in situations where the data can be enumerated, and they typically involve whole numbers.
Recommended video:
Guided course
04:48
Variance & Standard Deviation of Discrete Random Variables
Continuous Random Variables
Continuous random variables, in contrast, can take on an infinite number of values within a given range. They are often associated with measurements, such as height, weight, or temperature. These variables can be represented on a number line and can include fractions and decimals, making them uncountable.
Recommended video:
Guided course
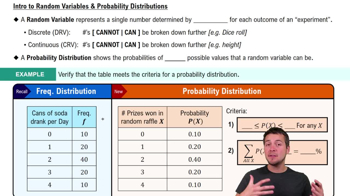
07:09Intro to Random Variables & Probability Distributions
Identifying Random Variables
To determine whether a random variable is discrete or continuous, one must analyze the nature of the data it represents. If the values can be listed or counted, it is discrete; if the values can vary continuously and include fractions, it is continuous. This distinction is crucial for selecting appropriate statistical methods for analysis.
Recommended video:
Guided course
07:09Intro to Random Variables & Probability Distributions
7:09mWatch next
Master Intro to Random Variables & Probability Distributions with a bite sized video explanation from Patrick
Start learningRelated Videos
Related Practice