Probabilities & Z-Scores w/ Graphing Calculator: Videos & Practice Problems

In probability and statistics, understanding how to find probabilities associated with z-scores is essential, especially when dealing with the standard normal distribution. A z-score indicates how many standard deviations an element is from the mean. To find probabilities from z-scores, one can utilize a z-table or a graphing calculator, which can simplify the process significantly.

When using a graphing calculator, such as the TI-84, the normalcdf and shade normal functions are particularly useful. The normalcdf function calculates the cumulative distribution function, which gives the probability that a standard normal random variable is less than a specified value. The shade normal function visually represents the area under the curve, making it easier to understand the probabilities involved.

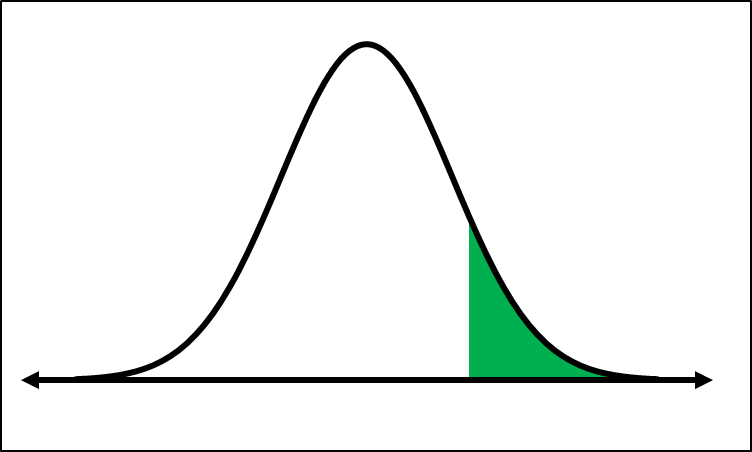
To find the probability that a z-score is less than a specific value, such as -0.81, you would set the lower bound to negative infinity (which can be approximated as -1E99) and the upper bound to the z-score in question. The calculator will then provide the area to the left of that z-score, which corresponds to the probability. For example, using the calculator, you would input:

lower bound: -1E99upper bound: -0.81mean (μ): 0standard deviation (σ): 1

After executing the function, the calculator will display the area, which in this case is approximately 0.2090, matching the value obtained from the z-table.

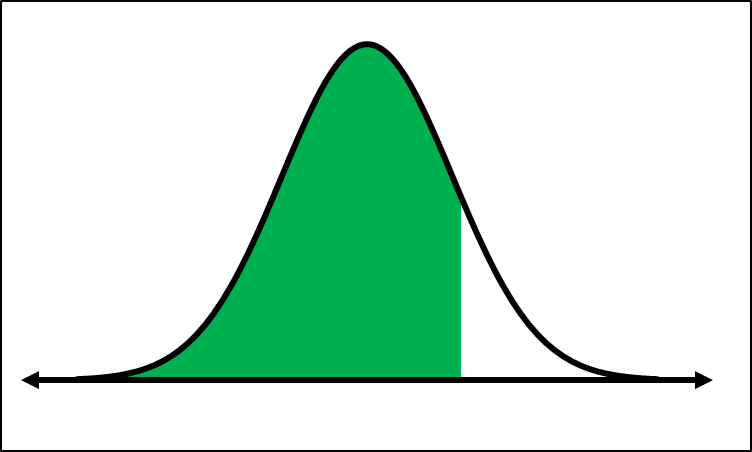
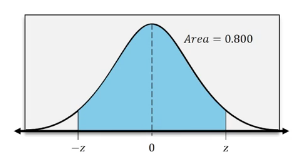
For scenarios where you need to find the probability between two z-scores, such as between -1 and 1, the process is similar but requires adjusting the bounds. Here, the lower bound would be -1 and the upper bound would be 1. This setup instructs the calculator to compute the area between these two z-scores. The resulting area, which represents the probability of a z-score falling within this range, is approximately 0.6827.

Utilizing a graphing calculator not only streamlines the process of finding probabilities associated with z-scores but also enhances accuracy by providing a visual representation of the data. This method is particularly beneficial for more complex problems where manual calculations may become cumbersome.

To find a z-score from a given probability using a TI-84 graphing calculator, you can utilize the inverse normal function. This process is essential when you have a probability and need to determine the corresponding z-score, particularly in the context of a standard normal distribution where the mean (μ) is 0 and the standard deviation (σ) is 1.

Start by sketching a normal distribution graph to visualize the area represented by the given probability. For instance, if you have a probability that z is less than some unknown z-score equal to 0.0853, this indicates a small area to the left of the z-score on the graph. Since this area is small, the z-score will be negative.

To calculate the z-score, follow these steps:

1. Open your calculator and press 2nd followed by VARS to access the distribution menu.
2. Select the inverse normal option (usually the third option).
3. Input the area (probability) you have, in this case, 0.0853. For a standard normal distribution, keep μ as 0 and σ as 1.
4. Choose the appropriate tail option. Since the area is to the left, select the left tail.
5. Press Paste and then Enter to obtain the z-score, which should be approximately -1.37.

In another scenario, if you have a probability that z is greater than some unknown number, such as 0.3409, you will need to adjust your approach. This probability represents an area to the right of the z-score. To visualize this, you would shade the area to the right on your graph, indicating that the z-score will be a small positive number.

For this calculation, repeat the steps above, but remember to change the tail option to the right since the area is to the right of the z-score. Input 0.3409 directly if you have a TI-84 Plus CE. If you are using a regular TI-84, you must first convert this probability to a left-tail probability by calculating 1 - 0.3409, which equals 0.6591. Then, input this value into the inverse normal function, select the left tail, and proceed to find the z-score, which should be around 0.41.

Understanding how to navigate these calculations with your TI-84 calculator is crucial for accurately interpreting probabilities and z-scores in statistics. Practice these steps to become proficient in using the inverse normal function for various probability scenarios.