Two Means - Matched Pairs (Dependent Samples): Videos & Practice Problems

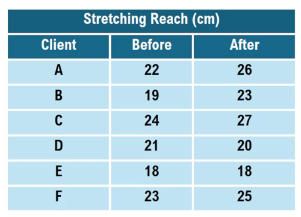
In statistical analysis, understanding the concept of matched pairs is crucial when conducting hypothesis tests involving two samples. Matched pairs occur when two samples are related in a specific way, allowing for a one-to-one pairing of values. This relationship can manifest in various forms, such as before-and-after comparisons of the same individual, comparisons between related individuals (like siblings or coworkers), or comparisons between self-reported data and measured data.

To determine if two samples are matched pairs, there are several criteria to consider. First, the sample sizes must be equal, as each value from one sample must correspond to a value in the other sample. Second, the samples must be related according to one of the established relationships mentioned earlier. Lastly, the values must be paired in a one-to-one relationship, meaning that it should make logical sense to compare specific values from each sample.

For example, if we analyze heart rates of individuals before and after sleeping, we can see that each individual's heart rate before sleep can be directly compared to their heart rate after sleep. This establishes a clear matched pair relationship. Conversely, if we compare heart rates between two different groups, such as males and females, the samples are not matched pairs because there is no direct relationship between the individuals in each group.

When working with matched pairs, one common calculation is to find the difference between the paired values, denoted as \(d\). This is done by subtracting one value from the other in a consistent order. For instance, if we subtract the after-sleep heart rate from the before-sleep heart rate, we can calculate the differences for each individual. The mean of these differences is represented as \(\bar{d}\), which can be calculated by summing all the differences and dividing by the number of pairs.

Additionally, the standard deviation of these differences, denoted as \(SD_d\), can be calculated to understand the variability of the differences. This statistical approach allows researchers to analyze the effects of interventions or changes over time effectively.

In summary, recognizing matched pairs is essential for accurate hypothesis testing. By ensuring that samples are related and appropriately paired, researchers can draw meaningful conclusions from their data.

Determining whether two samples are independent or matched pairs is crucial for selecting the appropriate hypothesis test. This distinction hinges on several key factors, including sample size, relationships between samples, and the pairing of values.

In the first scenario, a nutritionist measures the blood pressure of 30 patients before and after they start a new diet. Here, the sample sizes are equal, with 30 measurements taken before and 30 after the diet. The relationship between the samples is evident, as the same individuals are measured at two different times, creating a clear before-and-after relationship. This indicates that the values are paired one-to-one, as each patient's before measurement corresponds directly to their after measurement. Thus, this scenario represents matched pairs.

In the second scenario, a teacher administers a practice exam to 40 students and then gives a different group of 40 students the same exam a week later. Although the sample sizes are equal, the key difference lies in the lack of a direct relationship between the two groups. Each student's score cannot be paired with a specific score from the other group, as they are different students. Therefore, this scenario consists of independent samples.

The third scenario involves the same teacher giving the same 40 students a similar graded exam a week after the initial practice exam. Again, the sample sizes are equal, and there is a clear relationship since the same students are being tested twice. Each student's score from the first exam can be directly compared to their score on the second exam, establishing a one-to-one pairing. Consequently, this scenario is classified as matched pairs.

In summary, recognizing whether samples are independent or matched pairs is essential for hypothesis testing. Matched pairs involve related samples with a direct pairing, while independent samples consist of distinct groups without such relationships. Understanding these distinctions will enhance your ability to conduct appropriate statistical analyses.

Matched pairs hypothesis testing is a statistical method used to compare two related samples, often in a before-and-after scenario. This approach simplifies the process of hypothesis testing by focusing on the differences between paired observations rather than the individual means. In this context, we replace standard variables with their difference equivalents: the sample mean difference is denoted as \( \bar{d} \), the population mean difference as \( \mu_d \), and the sample standard deviation of the differences as \( s_d \).

To illustrate this, consider a study evaluating a new medication's effectiveness in reducing blood pressure. Researchers collected data from 37 patients, measuring their blood pressure before and 15 days after taking the medication. The sample mean difference in blood pressure was found to be \( \bar{d} = 3.2 \) mmHg, with a standard deviation of \( s_d = 6.7 \) mmHg. The goal is to determine if the medication significantly reduces blood pressure, using a significance level of \( \alpha = 0.05 \).

The first step in hypothesis testing is to establish the null and alternative hypotheses. The null hypothesis (\( H_0 \)) posits that there is no difference in blood pressure, or \( \mu_d = 0 \). Conversely, the alternative hypothesis (\( H_a \)) suggests that the medication does reduce blood pressure, represented as \( \mu_d > 0 \). This indicates that a positive mean difference supports the claim of reduced blood pressure.

Next, we calculate the test statistic using the formula for the t-score, which is given by:

\( t = \frac{\bar{d} - \mu_d}{s_d / \sqrt{n}} \)

In this case, substituting the known values yields:

\( t = \frac{3.2 - 0}{6.7 / \sqrt{37}} \approx 2.91 \)

With the t-score calculated, we determine the degrees of freedom, which for matched pairs is \( n - 1 \). Here, \( n = 37 \), so the degrees of freedom is \( 36 \). Using a t-distribution table or calculator, we find the p-value corresponding to \( t = 2.91 \) with 36 degrees of freedom. This results in a p-value of approximately \( 0.0031 \).

Finally, we compare the p-value to the significance level \( \alpha \). Since \( 0.0031 < 0.05 \), we reject the null hypothesis. This outcome indicates sufficient evidence to conclude that the medication is effective in reducing blood pressure.

In summary, matched pairs hypothesis testing allows for a straightforward analysis of differences between related samples, following a systematic approach to establish hypotheses, calculate test statistics, and interpret results. This method is particularly useful in clinical studies where the same subjects are measured before and after an intervention.

In hypothesis testing, particularly with matched pairs, the goal is to determine if there is a significant difference between two related groups. In this scenario, a professor randomly selects 12 students to compare their scores on a pop quiz and a scheduled quiz. Each student's scores are paired, and the difference between the two scores is calculated. The mean difference, denoted as \( \bar{d} \), is found to be -1.1, with a standard deviation of 1.8.

To begin the hypothesis test, we establish the null and alternative hypotheses. The null hypothesis (\( H_0 \)) typically states that there is no difference in the means, which in this case translates to \( \mu_d = 0 \). The alternative hypothesis (\( H_a \)) reflects the claim being tested. Here, the claim is that students perform worse on the pop quizzes than on the scheduled quizzes, indicating that the mean difference is less than zero. Thus, the alternative hypothesis is \( \mu_d < 0 \), signifying a left-tailed test.

Next, we calculate the test statistic using the formula for matched pairs. The test statistic \( t \) is calculated as follows:

\( t = \frac{\bar{d} - \mu_d}{s_d / \sqrt{n}} \)

In this formula, \( \bar{d} \) is the mean difference (-1.1), \( \mu_d \) is the mean difference under the null hypothesis (0), \( s_d \) is the standard deviation of the differences (1.8), and \( n \) is the number of pairs (12). Plugging in these values, we have:

\( t = \frac{-1.1 - 0}{1.8 / \sqrt{12}} \)

Calculating this gives a test statistic of approximately -2.12. This value indicates how many standard deviations the sample mean difference is from the hypothesized population mean difference under the null hypothesis.

In summary, we have established our null hypothesis \( H_0: \mu_d = 0 \) and alternative hypothesis \( H_a: \mu_d < 0 \), and calculated the test statistic \( t \approx -2.12 \). These steps are crucial in determining whether to reject the null hypothesis in favor of the alternative hypothesis based on further analysis, such as calculating the p-value.

In statistical analysis, matched pairs are used to compare two related samples, and creating a confidence interval for the mean difference is a common task. When constructing a confidence interval for matched pairs, the focus is on the difference between two values, specifically the population difference denoted as \( \mu_d \). The sample mean difference serves as the point estimator, which is the best estimate of this population parameter.

To illustrate this, consider a study evaluating the effectiveness of a new blood pressure medication. In this study, blood pressure readings were taken from 37 patients before and 15 days after medication. The sample mean difference (\( \bar{d} \)) was found to be 3.2, with a standard deviation of the differences (\( s_d \)) equal to 6.7. To create a 90% confidence interval, we first verify that the data consists of matched pairs and that the sample size is adequate (in this case, \( n = 37 \), which is greater than 30, allowing us to assume normality).

The next step involves determining the critical value from the t-distribution, which is necessary for calculating the margin of error. For a 90% confidence level, the critical value \( t_{\alpha/2} \) is found using the degrees of freedom, calculated as \( n - 1 \) (which equals 36 here). The critical t-value for 36 degrees of freedom at a 90% confidence level is approximately 1.688.

With the point estimator \( \bar{d} = 3.2 \) established, we can now calculate the margin of error using the formula:

\[ \text{Margin of Error} = t_{\alpha/2} \times \frac{s_d}{\sqrt{n}} \]

Substituting the values, we find:

\[ \text{Margin of Error} = 1.688 \times \frac{6.7}{\sqrt{37}} \approx 1.85 \]

To construct the confidence interval, we add and subtract the margin of error from the point estimator:

\[ \text{Lower Bound} = \bar{d} - \text{Margin of Error} = 3.2 - 1.85 = 1.35 \]

\[ \text{Upper Bound} = \bar{d} + \text{Margin of Error} = 3.2 + 1.85 = 5.05 \]

Thus, the 90% confidence interval for the mean difference in blood pressure before and after taking the medication is \( (1.35, 5.05) \).

Interpreting this result in the context of hypothesis testing, we assess the claim that there is no difference in blood pressure after medication. Since the confidence interval does not include zero, we reject the null hypothesis, indicating that there is significant evidence to suggest a difference in blood pressure before and after taking the medication. Therefore, we conclude that the medication has a statistically significant effect on blood pressure.