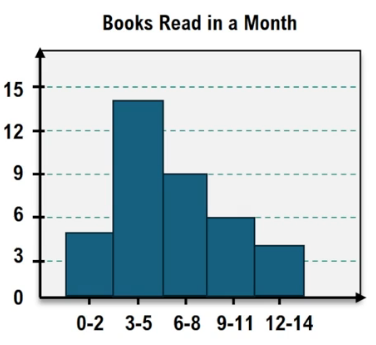
Histograms: Videos & Practice Problems

Histograms are a powerful tool for visualizing quantitative data, serving as a graphical representation of frequency distributions. A frequency distribution organizes data into classes or bins, allowing for easier identification of patterns and trends compared to raw numerical tables. To create a histogram, one must first establish a frequency distribution table, which lists the classes and their corresponding frequencies.

In constructing a histogram, the x-axis represents the class midpoints, calculated by averaging the upper and lower limits of each class. For example, for a class range of 20 to 29, the midpoint would be \( \frac{20 + 29}{2} = 24.5 \). The y-axis displays the frequencies, denoted as \( f \), which indicate how many data points fall within each class. Bars are then drawn for each class, with heights corresponding to their frequencies. It is important that these bars touch, as this visually emphasizes the continuous nature of the data.

When analyzing the shape of a histogram, there are four common distribution types to consider: normal, skewed right, skewed left, and uniform. A normal distribution is characterized by a bell-shaped curve, where data is symmetrically distributed around the mean, with most values clustering around the center. In contrast, a skewed right distribution has a peak on the left and a tail extending to the right, often seen in income data where a few high earners skew the average. Conversely, a skewed left distribution peaks on the right and trails off to the left, commonly observed in life expectancy data. Lastly, a uniform distribution occurs when all classes have approximately equal frequencies, such as in the case of rolling dice.

By examining the shape of a histogram, one can determine the underlying distribution of the data. For instance, if a histogram peaks in the middle and tapers off symmetrically, it indicates a normal distribution. Understanding these concepts is crucial for effectively interpreting data and making informed decisions based on statistical analysis.

In data analysis, transforming a dataset into a frequency distribution and then visualizing it with a histogram can be a tedious process, especially with larger datasets. However, using a TI-84 graphing calculator can significantly streamline this process, allowing for quicker insights into the shape of the distribution, such as whether it is normal or skewed.

To begin, input your dataset into the calculator. Access the statistics menu by pressing the STAT button, then select EDIT. Here, you can enter your data points into a list. For instance, if you have study times for students, simply type each number followed by ENTER. After entering all data points, you should see a confirmation indicating the total number of entries.

Next, to create a histogram, access the STAT PLOT by pressing 2nd followed by the Y= button. Turn on the plot and select the histogram option, which is a bar graph. The calculator will automatically reference the list you populated. After setting this up, exit to the main screen by pressing 2nd and then MODE.

To ensure the histogram accurately represents your data, adjust the viewing window. Press the ZOOM button and select 9: ZoomStat, which automatically optimizes the window for your data. You can further refine the histogram by adjusting the class width. Access the WINDOW settings and set the XSCL (x scale) to your desired class width, such as 15. Additionally, set the Xmin to the minimum value of your dataset and the Xmax to a value slightly above the maximum.

After these adjustments, return to the graph function to view your updated histogram. Utilize the TRACE function to examine the frequencies and class limits. This will help you analyze the distribution's characteristics. For instance, if the histogram shows a peak towards the left and a tail extending to the right, the distribution is skewed to the right. Conversely, if it peaks to the right, it would be skewed to the left.

In summary, using a TI-84 calculator to create histograms allows for efficient data visualization and analysis. By following these steps, you can quickly determine the nature of your dataset's distribution, whether it is normal, skewed, or uniform, enhancing your understanding of the underlying data trends.