Family/Partner Groups of people aged 15–65 are randomly select...

Question

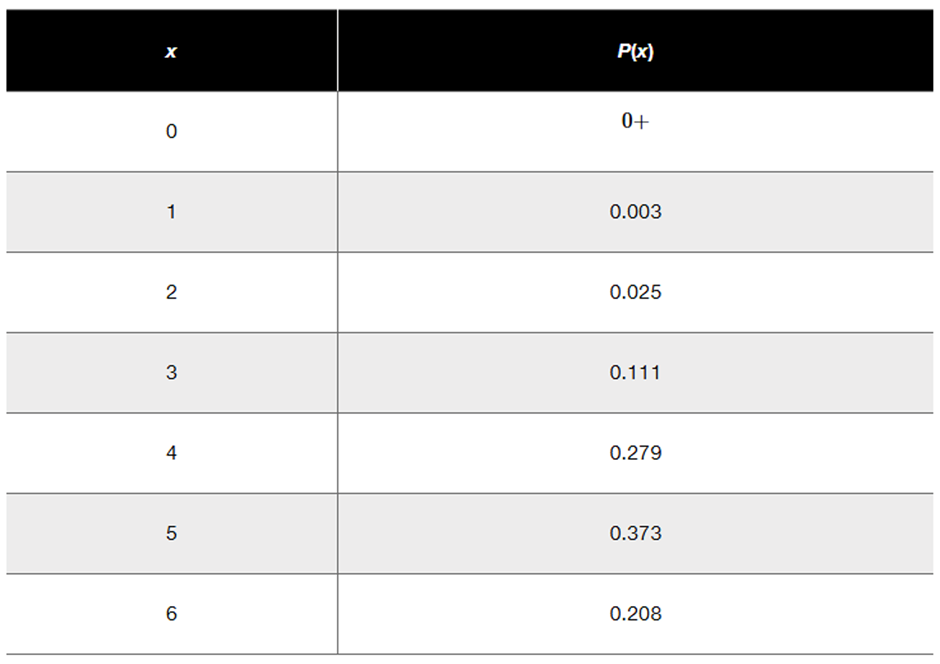
Family/Partner Groups of people aged 15–65 are randomly selected and arranged in groups of six. The random variable x is the number in the group who say that their family and/or partner contribute most to their happiness (based on a Coca-Cola survey). The accompanying table lists the values of x along with their corresponding probabilities. Does the table describe a probability distribution? If so, find the mean and standard deviation.

Table showing x values 0-6 with probabilities: 0+, 0.003, 0.025, 0.111, 0.279, 0.373, 0.208.

Accepted Answer

Hello, everyone, let's take a look at this question together. During a health survey, people are arranged in groups of 5 and asked if they exercise regularly. The random variable X denotes the number of people in each group who say yes. The given probabilities for X equals 012, 3, 45 are 0.05, 0.15, 0.30, 0.30, 0.15, and 0.05 respectively. Confirm if this is a probability distribution and find the mean and standard deviation. Is it answer choice A? Yes, it is a probability distribution. The mean is 2.5, and the standard deviation is 1.2. Answer choice B, no, it is not a probability distribution. The mean is 2.5, and the standard deviation is 1.4. Answer choice C yes. It is a probability distribution. The mean is 3, and the standard deviation is 1.4, or answer choice D no, it is not a probability distribution. The mean is 2, and the standard deviation is 1.2. So in order to solve this question, we must first check for probability distribution. Which can be done by calculating the sum of the probabilities which from the information provided in the question, we add together all of our probabilities, which equals one, which the value of one confirms it's a valid probability distribution. Then the next step is to calculate the mean. Which the mean can be calculated using the formula for the mean, where mu is equal to the sum of X multiplied by P of X, and plugging in our values into the formula for the mean, we get the value of 2.5 for the mean. And then we can find the standard deviation, which we must first find sigma squared using the formula for sigma squared, which is equal to the sum of the squared difference between X and the mean multiplied by P of X, and calculating the values in our table to find sigma squared. Plugging in the values into the sigma squared formula gives us 1.45 as the value for sigma squared. And since we are trying to find the standard deviation, which is equal to sigma, we need to take the square root of sigma squared, which is 1.45, and the square root of sigma or 1.45 is equal to 1.20. Therefore, 1.20 is the value of the standard deviation. So we know that it is a probability distribution, the mean is equal. To 2.5, and the standard deviation is equal to 1.2, which looking at our answer choices, we can identify that answer choice A is the correct answer, as it contains all of the correct values for the calculations that we have made for this question, making answer choice A the only correct answer choice. I hope you found this video to be helpful. Thank you and goodbye.

Key Concepts

Probability Distribution

Mean of a Probability Distribution

Standard Deviation of a Probability Distribution

Watch next