Is Friday the 13th Unlucky? Listed below are numbers of hospital admissions in one region due to traffic accidents on different Fridays falling on the 6th day of a month and the following 13th day of the month (based on data from “Is Friday the 13th Bad for Your Health,” by Scanlon et al., British Medical Journal, Vol. 307). Assume that we want to use a 0.05 significance level to test the claim that the data support the claim that fewer hospital admissions due to traffic accidents occur on Friday the 6th than on the following Friday the 13th. Identify the null hypothesis and alternative hypothesis.
Table of contents
- 1. Intro to Stats and Collecting Data1h 14m
- 2. Describing Data with Tables and Graphs1h 55m
- 3. Describing Data Numerically2h 5m
- 4. Probability2h 16m
- 5. Binomial Distribution & Discrete Random Variables3h 6m
- 6. Normal Distribution and Continuous Random Variables2h 11m
- 7. Sampling Distributions & Confidence Intervals: Mean3h 23m
- Sampling Distribution of the Sample Mean and Central Limit Theorem19m
- Distribution of Sample Mean - Excel23m
- Introduction to Confidence Intervals15m
- Confidence Intervals for Population Mean1h 18m
- Determining the Minimum Sample Size Required12m
- Finding Probabilities and T Critical Values - Excel28m
- Confidence Intervals for Population Means - Excel25m
- 8. Sampling Distributions & Confidence Intervals: Proportion1h 12m
- 9. Hypothesis Testing for One Sample3h 29m
- 10. Hypothesis Testing for Two Samples4h 50m
- Two Proportions1h 13m
- Two Proportions Hypothesis Test - Excel28m
- Two Means - Unknown, Unequal Variance1h 3m
- Two Means - Unknown Variances Hypothesis Test - Excel12m
- Two Means - Unknown, Equal Variance15m
- Two Means - Unknown, Equal Variances Hypothesis Test - Excel9m
- Two Means - Known Variance12m
- Two Means - Sigma Known Hypothesis Test - Excel21m
- Two Means - Matched Pairs (Dependent Samples)42m
- Matched Pairs Hypothesis Test - Excel12m
- 11. Correlation1h 6m
- 12. Regression1h 50m
- 13. Chi-Square Tests & Goodness of Fit1h 57m
- 14. ANOVA1h 57m
9. Hypothesis Testing for One Sample
Steps in Hypothesis Testing
Problem 9.3.3a
Textbook Question
Confidence Interval Assume that we want to use the sample data in Exercise 1 for constructing a confidence interval to be used for testing the given claim.
a. What is the confidence level that should be used for the confidence interval?
 Verified step by step guidance
Verified step by step guidance1
Identify the confidence level based on the context of the problem. Typically, the confidence level is determined by the significance level (α) used in hypothesis testing. For example, if α = 0.05, the confidence level is 1 - α = 0.95 or 95%.
Review the problem or any accompanying information to determine if a specific significance level (α) is provided. If not explicitly stated, assume a common value such as α = 0.05 (95% confidence) or α = 0.01 (99% confidence).
Understand that the confidence level represents the proportion of confidence intervals that would contain the true population parameter if the procedure were repeated many times.
If the problem involves a two-tailed test, ensure that the confidence level corresponds to the total area outside the tails (e.g., for α = 0.05, the confidence level is 95%).
Conclude by stating the confidence level to be used for constructing the confidence interval, based on the information provided or the standard assumptions in hypothesis testing.
 Verified video answer for a similar problem:
Verified video answer for a similar problem:This video solution was recommended by our tutors as helpful for the problem above
Video duration:
1mPlay a video:
Was this helpful?
Key Concepts
Here are the essential concepts you must grasp in order to answer the question correctly.
Confidence Level
The confidence level represents the degree of certainty that the true population parameter lies within the confidence interval. Common confidence levels are 90%, 95%, and 99%, indicating the proportion of times the interval would capture the true parameter if the same sampling method were repeated multiple times.
Recommended video:
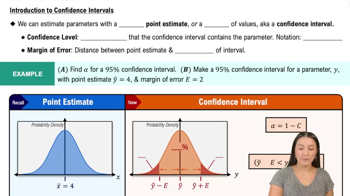
Introduction to Confidence Intervals
Confidence Interval
A confidence interval is a range of values derived from sample data that is likely to contain the true population parameter. It is calculated using the sample mean, standard deviation, and the critical value corresponding to the chosen confidence level, providing a measure of uncertainty around the estimate.
Recommended video:

Introduction to Confidence Intervals
Sample Data
Sample data refers to the subset of observations drawn from a larger population, used to make inferences about that population. The quality and size of the sample affect the reliability of the confidence interval, as larger and more representative samples tend to yield more accurate estimates of the population parameters.
Recommended video:
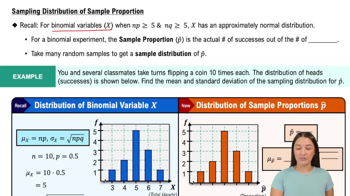
Sampling Distribution of Sample Proportion

 6:21m
6:21mWatch next
Master Step 1: Write Hypotheses with a bite sized video explanation from Patrick
Start learningRelated Videos
Related Practice
Textbook Question
