Here are the essential concepts you must grasp in order to answer the question correctly.
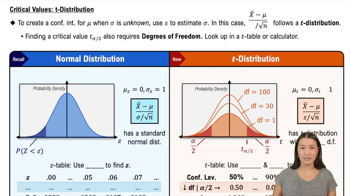
Critical Value (t-distribution)
The critical value, denoted as tα/2, is a point on the t-distribution that corresponds to a specified confidence level. It is used to determine the margin of error in confidence intervals, especially when the sample size is small or the population standard deviation is unknown. For a 99% confidence level, this value is found using statistical tables or software, reflecting the area in the tails of the distribution.
Recommended video:
Critical Values: t-Distribution
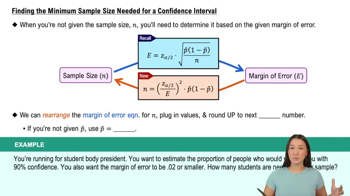
Margin of Error
The margin of error quantifies the uncertainty associated with a sample estimate. It is calculated by multiplying the critical value by the standard error of the sample mean. This value indicates the range within which the true population parameter is expected to lie, providing a buffer around the sample mean to account for sampling variability.
Recommended video:
Finding the Minimum Sample Size Needed for a Confidence Interval
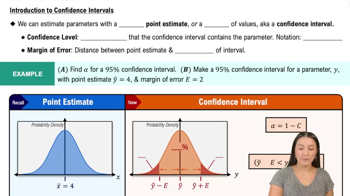
Confidence Interval
A confidence interval is a range of values derived from sample statistics that is likely to contain the true population parameter. It is constructed using the sample mean and the margin of error, providing an interval estimate rather than a point estimate. The width of the interval reflects the level of confidence; a higher confidence level results in a wider interval, indicating greater uncertainty about the exact value of the parameter.
Recommended video:
Introduction to Confidence Intervals