Heights of Presidents Refer to Data Set 22 “Presidents” in Appendix B. Treat the data as a sample and find the proportion of presidents who were taller than their opponents. Use that result to construct a 95% confidence interval estimate of the population percentage. Based on the result, does it appear that greater height is an advantage for presidential candidates? Why or why not?
Table of contents
- 1. Intro to Stats and Collecting Data1h 14m
- 2. Describing Data with Tables and Graphs1h 55m
- 3. Describing Data Numerically2h 5m
- 4. Probability2h 16m
- 5. Binomial Distribution & Discrete Random Variables3h 6m
- 6. Normal Distribution and Continuous Random Variables2h 11m
- 7. Sampling Distributions & Confidence Intervals: Mean3h 23m
- Sampling Distribution of the Sample Mean and Central Limit Theorem19m
- Distribution of Sample Mean - Excel23m
- Introduction to Confidence Intervals15m
- Confidence Intervals for Population Mean1h 18m
- Determining the Minimum Sample Size Required12m
- Finding Probabilities and T Critical Values - Excel28m
- Confidence Intervals for Population Means - Excel25m
- 8. Sampling Distributions & Confidence Intervals: Proportion1h 12m
- 9. Hypothesis Testing for One Sample3h 29m
- 10. Hypothesis Testing for Two Samples4h 50m
- Two Proportions1h 13m
- Two Proportions Hypothesis Test - Excel28m
- Two Means - Unknown, Unequal Variance1h 3m
- Two Means - Unknown Variances Hypothesis Test - Excel12m
- Two Means - Unknown, Equal Variance15m
- Two Means - Unknown, Equal Variances Hypothesis Test - Excel9m
- Two Means - Known Variance12m
- Two Means - Sigma Known Hypothesis Test - Excel21m
- Two Means - Matched Pairs (Dependent Samples)42m
- Matched Pairs Hypothesis Test - Excel12m
- 11. Correlation1h 6m
- 12. Regression1h 50m
- 13. Chi-Square Tests & Goodness of Fit1h 57m
- 14. ANOVA1h 57m
8. Sampling Distributions & Confidence Intervals: Proportion
Confidence Intervals for Population Proportion
Problem 7.1.33c
Textbook Question
E-Cigarettes A New York Times article reported that a survey conducted in 2014 included 36,000 adults, with 3.7% of them being regular users of e-cigarettes. Because e-cigarette use is relatively new, there is a need to obtain today’s usage rate. How many adults must be surveyed now if we want a confidence level of 95% and a margin of error of 1.5 percentage points?
c. Does the use of the result from the 2014 survey have much of an effect on the sample size?
 Verified step by step guidance
Verified step by step guidance1
Step 1: Understand the problem. We are tasked with determining the sample size required to estimate the proportion of adults who are regular users of e-cigarettes with a 95% confidence level and a margin of error of 1.5 percentage points. Additionally, we need to consider whether the 2014 survey result (3.7%) affects the sample size calculation.
Step 2: Recall the formula for sample size calculation for proportions: \( n = \frac{{Z^2 \cdot p \cdot (1-p)}}{{E^2}} \), where \( Z \) is the z-score corresponding to the confidence level, \( p \) is the estimated proportion, and \( E \) is the margin of error.
Step 3: Identify the values needed for the formula. For a 95% confidence level, the z-score \( Z \) is approximately 1.96. The margin of error \( E \) is given as 1.5 percentage points, which should be converted to a decimal (0.015). The proportion \( p \) can be taken from the 2014 survey result (3.7%, or 0.037), but we should also consider the worst-case scenario where \( p \) is 0.5 (maximum variability).
Step 4: Calculate the sample size using both \( p = 0.037 \) and \( p = 0.5 \). Substitute the values into the formula \( n = \frac{{Z^2 \cdot p \cdot (1-p)}}{{E^2}} \). Perform the calculation for each case to see how the choice of \( p \) affects the sample size.
Step 5: Compare the results. Discuss whether using the 2014 survey proportion (3.7%) significantly reduces the sample size compared to using \( p = 0.5 \). This will help determine if the prior survey data has a substantial effect on the sample size calculation.
 Verified video answer for a similar problem:
Verified video answer for a similar problem:This video solution was recommended by our tutors as helpful for the problem above
Video duration:
3mPlay a video:
Was this helpful?
Key Concepts
Here are the essential concepts you must grasp in order to answer the question correctly.
Sample Size Calculation
Sample size calculation is a statistical method used to determine the number of observations or replicates needed in a study to achieve a desired level of precision. It takes into account the population size, the expected proportion of the attribute of interest, the desired confidence level, and the margin of error. In this case, the calculation will help determine how many adults need to be surveyed to estimate the current e-cigarette usage rate accurately.
Recommended video:
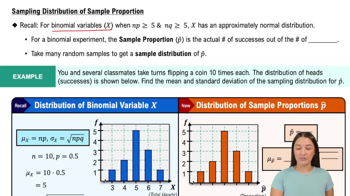
Sampling Distribution of Sample Proportion
Confidence Level
The confidence level represents the degree of certainty that the true population parameter lies within the confidence interval calculated from the sample data. A 95% confidence level means that if the same survey were conducted multiple times, approximately 95% of the calculated intervals would contain the true population proportion. This concept is crucial for understanding the reliability of the survey results.
Recommended video:
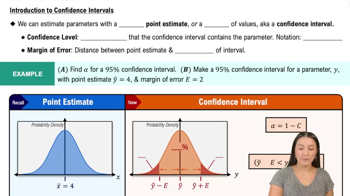
Introduction to Confidence Intervals
Margin of Error
The margin of error quantifies the amount of random sampling error in a survey's results. It indicates the range within which the true population parameter is expected to fall, based on the sample data. A smaller margin of error requires a larger sample size, which is important for ensuring that the survey results are precise and reflect the current usage rate of e-cigarettes accurately.
Recommended video:
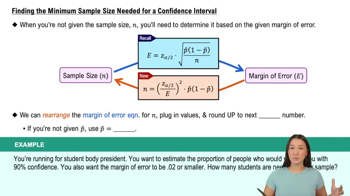
Finding the Minimum Sample Size Needed for a Confidence Interval

 5:45m
5:45mWatch next
Master Constructing Confidence Intervals for Proportions with a bite sized video explanation from Patrick
Start learningRelated Videos
Related Practice
Textbook Question
