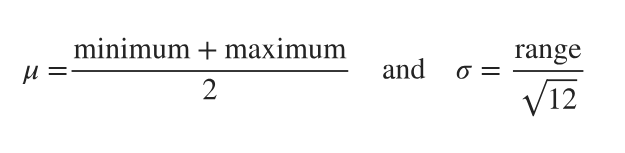Mensa Membership in Mensa requires a score in the top 2% on a standard intelligence test. The Wechsler IQ test is designed for a mean of 100 and a standard deviation of 15, and scores are normally distributed.

c. If 4 subjects take the Wechsler IQ test and they have a mean of 131 but the individual scores are lost, can we conclude that all 4 of them have scores of at least 131?

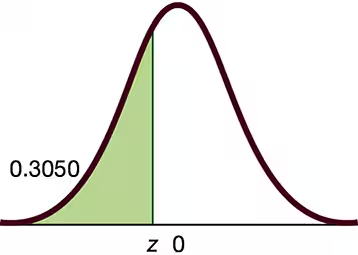
Standard Normal Distribution. In Exercises 13–16, find the indicated z score. The graph depicts the standard normal distribution of bone density scores with mean 0 and standard deviation 1.

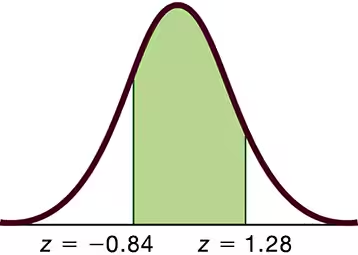
Basis for the Range Rule of Thumb and the Empirical Rule. In Exercises 45–48, find the indicated area under the curve of the standard normal distribution; then convert it to a percentage and fill in the blank. The results form the basis for the range rule of thumb and the empirical rule introduced in Section 3-2.

About __ % of the area is between z = -1 and z = 1 (or within 1 standard deviation of the mean).

Standard Normal Distribution. In Exercises 17–36, assume that a randomly selected subject is given a bone density test. Those test scores are normally distributed with a mean of 0 and a standard deviation of 1. In each case, draw a graph, then find the probability of the given bone density test scores. If using technology instead of Table A-2, round answers to four decimal places.

Between 1.50 and 2.00

Standard Normal Distribution. In Exercises 9–12, find the area of the shaded region. The graph depicts the standard normal distribution of bone density scores with mean 0 and standard deviation 1.

Standard Normal Distribution. In Exercises 17–36, assume that a randomly selected subject is given a bone density test. Those test scores are normally distributed with a mean of 0 and a standard deviation of 1. In each case, draw a graph, then find the probability of the given bone density test scores. If using technology instead of Table A-2, round answers to four decimal places.

Less than -2.00

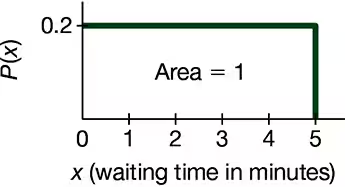
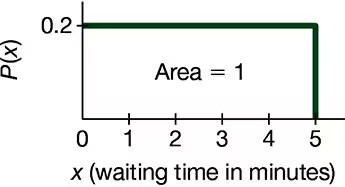
Continuous Uniform Distribution. In Exercises 5–8, refer to the continuous uniform distribution depicted in Figure 6-2 and described in Example 1. Assume that a passenger is randomly selected, and find the probability that the waiting time is within the given range.

Greater than 3.00 minutes

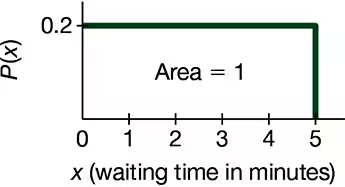
Continuous Uniform Distribution. In Exercises 5–8, refer to the continuous uniform distribution depicted in Figure 6-2 and described in Example 1. Assume that a passenger is randomly selected, and find the probability that the waiting time is within the given range.

Less than 4.00 minutes

Continuous Uniform Distribution. In Exercises 5–8, refer to the continuous uniform distribution depicted in Figure 6-2 and described in Example 1. Assume that a passenger is randomly selected, and find the probability that the waiting time is within the given range.

Between 2 minutes and 3 minutes

Distributions In a continuous uniform distribution,

a. Find the mean and standard deviation for the distribution of the waiting times represented in Figure 6-2, which accompanies Exercises 5–8.

Finding Bone Density Scores. In Exercises 37–40 assume that a randomly selected subject is given a bone density test. Bone density test scores are normally distributed with a mean of 0 and a standard deviation of 1. In each case, draw a graph, then find the bone density test score corresponding to the given information. Round results to two decimal places.

Find P99, the 99th percentile. This is the bone density score separating the bottom 99% from the top 1%.

Finding Bone Density Scores. In Exercises 37–40 assume that a randomly selected subject is given a bone density test. Bone density test scores are normally distributed with a mean of 0 and a standard deviation of 1. In each case, draw a graph, then find the bone density test score corresponding to the given information. Round results to two decimal places.

Find the bone density scores that are the quartiles Q1, Q2, and Q3.

Critical Values. In Exercises 41–44, find the indicated critical value. Round results to two decimal places.

z0.90

Basis for the Range Rule of Thumb and the Empirical Rule. In Exercises 45–48, find the indicated area under the curve of the standard normal distribution; then convert it to a percentage and fill in the blank. The results form the basis for the range rule of thumb and the empirical rule introduced in Section 3-2.

About __ % of the area is between z = -3.5 and z = 3.5 (or within 3.5 standard deviation of the mean).

Significance For bone density scores that are normally distributed with a mean of 0 and a standard deviation of 1, find the percentage of scores that are

c. not significant (or less than 2 standard deviations away from the mean).

In Exercises 25–28, use these parameters (based on Data Set 1 “Body Data” in Appendix B):

Men’s heights are normally distributed with mean 68.6 in. and standard deviation 2.8 in.

Women’s heights are normally distributed with mean 63.7 in. and standard deviation 2.9 in.

If the Navy changes the height requirements so that all women are eligible except the shortest 3% and the tallest 3%, what are the new height requirements for women?

IQ Scores. In Exercises 5–8, find the area of the shaded region. The graphs depict IQ scores of adults, and those scores are normally distributed with a mean of 100 and a standard deviation of 15 (as on the Wechsler IQ test).

IQ Scores. In Exercises 5–8, find the area of the shaded region. The graphs depict IQ scores of adults, and those scores are normally distributed with a mean of 100 and a standard deviation of 15 (as on the Wechsler IQ test).

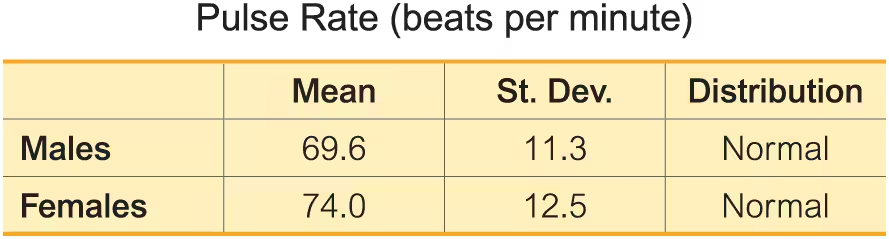
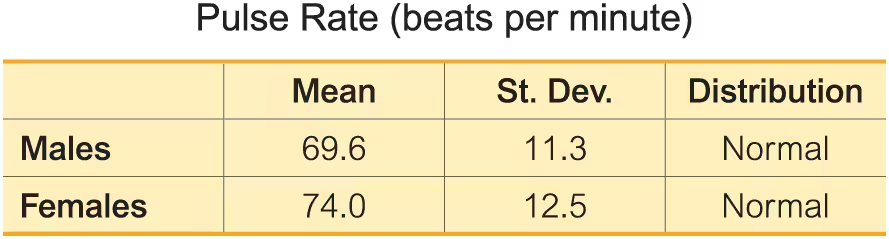
Pulse Rates. In Exercises 13–24, use the data in the table below for pulse rates of adult males and females (based on Data Set 1 “Body Data” in Appendix B). Hint: Draw a graph in each case.

Find the probability that a male has a pulse rate between 70 beats per minute and 90 beats per minute.

Pulse Rates. In Exercises 13–24, use the data in the table below for pulse rates of adult males and females (based on Data Set 1 “Body Data” in Appendix B). Hint: Draw a graph in each case.

For males, find P90 which is the pulse rate separating the bottom 90% from the top 10%.

Curving Test Scores A professor gives a test and the scores are normally distributed with a mean of 60 and a standard deviation of 12. She plans to curve the scores.

a. If she curves by adding 15 to each grade, what is the new mean and standard deviation?

Curving Test Scores A professor gives a test and the scores are normally distributed with a mean of 60 and a standard deviation of 12. She plans to curve the scores.

c. If the grades are curved so that grades of B are given to scores above the bottom 70% and below the top 10%, find the numerical limits for a grade of B.

Outliers For the purposes of constructing modified boxplots as described in Section 3-3, outliers are defined as data values that are above Q3 by an amount greater than 1.5 x IQR or below Q1 by an amount greater than 1.5 x IQR, where IQR is the interquartile range. Using this definition of outliers, find the probability that when a value is randomly selected from a normal distribution, it is an outlier.

Hershey Kisses Based on Data Set 38 “Candies” in Appendix B, weights of the chocolate in Hershey Kisses are normally distributed with a mean of 4.5338 g and a standard deviation of 0.1039 g.

a. What are the values of the mean and standard deviation after converting all weights of Hershey Kisses to z scores using z = (x - μ)/σ ?

b. The original weights are in grams. What are the units of the corresponding z scores?

Hershey Kisses Based on Data Set 38 “Candies” in Appendix B, weights of the chocolate in Hershey Kisses are normally distributed with a mean of 4.5338 g and a standard deviation of 0.1039 g

b. What is the value of the median?

Hershey Kisses Based on Data Set 38 “Candies” in Appendix B, weights of the chocolate in Hershey Kisses are normally distributed with a mean of 4.5338 g and a standard deviation of 0.1039 g

d. What is the value of the variance?

In Exercises 7–10, use the same population of {4, 5, 9} that was used in Examples 2 and 5. As in Examples 2 and 5, assume that samples of size n = 2 are randomly selected with replacement.

Sampling Distribution of the Sample Standard Deviation For the following, round results to three decimal places.

a. Find the value of the population standard deviation σ.

Good Sample? An economist is investigating the incomes of college students. Because she lives in Maine, she obtains sample data from that state. Is the resulting mean income of college students a good estimator of the mean income of college students in the United States? Why or why not?

Fatal Car Crashes There are about 15,000 car crashes each day in the United States, and the proportion of car crashes that are fatal is 0.00559 (based on data from the National Highway Traffic Safety Administration). Assume that each day, 1000 car crashes are randomly selected and the proportion of fatal car crashes is recorded.

a. What do you know about the mean of the sample proportions?

College Presidents There are about 4200 college presidents in the United States, and they have annual incomes with a distribution that is skewed instead of being normal. Many different samples of 40 college presidents are randomly selected, and the mean annual income is computed for each sample.

a. What is the approximate shape of the distribution of the sample means (uniform, normal, skewed, other)?