Here are the essential concepts you must grasp in order to answer the question correctly.
Normal Distribution
Normal distribution is a probability distribution that is symmetric about the mean, showing that data near the mean are more frequent in occurrence than data far from the mean. It is characterized by its bell-shaped curve, defined by its mean and standard deviation. In this context, the bone density scores are normally distributed with a mean of 0 and a standard deviation of 1, which allows for the application of statistical methods to find specific percentiles.
Recommended video:
Finding Standard Normal Probabilities using z-Table
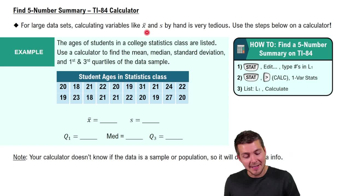
Quartiles
Quartiles are values that divide a dataset into four equal parts, each containing 25% of the data. The first quartile (Q1) is the median of the lower half of the data, the second quartile (Q2) is the median of the dataset, and the third quartile (Q3) is the median of the upper half. In the context of the bone density scores, finding Q1, Q2, and Q3 involves determining the corresponding z-scores that represent these quartiles in the normal distribution.
Recommended video:
Find 5-Number Summary - TI-84 Calculator
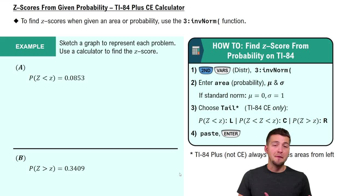
Z-scores
A z-score indicates how many standard deviations an element is from the mean. In a standard normal distribution, z-scores can be used to find probabilities and percentiles. For the bone density scores, calculating the z-scores for Q1, Q2, and Q3 allows us to determine the specific scores that correspond to these quartiles, facilitating the interpretation of the distribution of bone density test results.
Recommended video:
Z-Scores From Given Probability - TI-84 (CE) Calculator