Constructing Normal Quantile Plots. In Exercises 17–20, use the given data values to identify the corresponding z scores that are used for a normal quantile plot, then identify the coordinates of each point in the normal quantile plot. Construct the normal quantile plot, then determine whether the data appear to be from a population with a normal distribution.

Earthquake Depths A sample of depths (km) of earthquakes is obtained from Data Set 24 “Earthquakes” in Appendix B: 17.3, 7.0, 7.0, 7.0, 8.1, 6.8.

Transformations The heights (in inches) of women listed in Data Set 1 “Body Data” in Appendix B have a distribution that is approximately normal, so it appears that those heights are from a normally distributed population.

a. If 2 inches is added to each height, are the new heights also normally distributed?

Transformations The heights (in inches) of women listed in Data Set 1 “Body Data” in Appendix B have a distribution that is approximately normal, so it appears that those heights are from a normally distributed population.

b. If each height is converted from inches to centimeters, are the heights in centimeters also normally distributed?

Interpreting Normal Quantile Plots. In Exercises 5–8, examine the normal quantile plot and determine whether the sample data appear to be from a population with a normal distribution.

Ages of Presidents The normal quantile plot represents the ages of presidents of the United States at the times of their inaugurations. The data are from Data Set 22 “Presidents” in Appendix B.

Determining Normality. In Exercises 9–12, refer to the indicated sample data and determine whether they appear to be from a population with a normal distribution. Assume that this requirement is loose in the sense that the population distribution need not be exactly normal, but it must be a distribution that is roughly bell-shaped.

Taxi Trips The distances (miles) traveled by New York City taxis transporting customers, as listed in Data Set 32 “Taxis” in Appendix B

Determining Normality. In Exercises 9–12, refer to the indicated sample data and determine whether they appear to be from a population with a normal distribution. Assume that this requirement is loose in the sense that the population distribution need not be exactly normal, but it must be a distribution that is roughly bell-shaped.

Dunkin’ Donuts The drive-through service times (seconds) of Dunkin’ Donuts lunch customers, as listed in Data Set 36 “Fast Food” in Appendix B

Satisfying Requirements Data Set 1 “Body Data” in Appendix B includes a sample of 147 pulse rates of randomly selected women. Does that sample satisfy the following requirement: (1) The sample appears to be from a normally distributed population; or (2) the sample has a size of n>30?

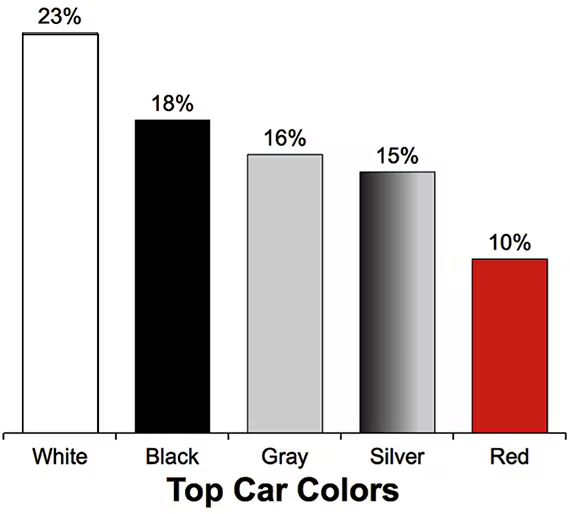
Car Colors

In Exercises 9–12, assume that 100 cars are randomly selected. Refer to the accompanying graph, which shows the top car colors and the percentages of cars with those colors (based on PPG Industries).

Black Cars Find the probability that at least 25 cars are black. Is 25 a significantly high number of black cars?

Notation Common tests such as the SAT, ACT, LSAT, and MCAT tests use multiple choice test questions, each with possible answers of a, b, c, d, e, and each question has only one correct answer. For people who make random guesses for answers to a block of 100 questions, identify the values of p, q, μ, and σ. What do μ and σ measure?

Tennis Replay In a recent year, there were 879 challenges made to referee calls in professional tennis singles play. Among those challenges, 231 challenges were upheld with the call overturned. Assume that in general, 25% of the challenges are successfully upheld with the call overturned.

a. If the 25% rate is correct, find the probability that among the 879 challenges, the number of overturned calls is exactly 231.

Continuity Correction In testing the assumption that the probability of a baby boy is 0.512, a geneticist obtains a random sample of 1000 births and finds that 502 of them are boys. Using the continuity correction, describe the area under the graph of a normal distribution corresponding to the following. (For example, the area corresponding to “the probability of at least 502 boys” is this: the area to the right of 501.5.)

a. The probability of 502 or fewer boys

Continuity Correction In testing the assumption that the probability of a baby boy is 0.512, a geneticist obtains a random sample of 1000 births and finds that 502 of them are boys. Using the continuity correction, describe the area under the graph of a normal distribution corresponding to the following. (For example, the area corresponding to “the probability of at least 502 boys” is this: the area to the right of 501.5.)

c. The probability of more than 502 boys

Smartphones Based on an LG smartphone survey, assume that 51% of adults with smartphones use them in theaters. In a separate survey of 250 adults with smartphones, it is found that 109 use them in theaters.

a. If the 51% rate is correct, find the probability of getting 109 or fewer smartphone owners who use them in theaters.

Eye Color Based on a study by Dr. P. Sorita at Indiana University, assume that 12% of us have green eyes. In a study of 650 people, it is found that 86 of them have green eyes.

b. Is 86 people with green eyes significantly high?

Mendelian Genetics When Mendel conducted his famous genetics experiments with peas, one sample of offspring consisted of 929 peas, with 705 of them having red flowers. If we assume, as Mendel did, that under these circumstances, there is a 3/4 probability that a pea will have a red flower, we would expect that 696.75 (or about 697) of the peas would have red flowers, so the result of 705 peas with red flowers is more than expected.

a. If Mendel’s assumed probability is correct, find the probability of getting 705 or more peas with red flowers.

Sleepwalking Assume that 29.2% of people have sleepwalked (based on “Prevalence and Comorbidity of Nocturnal Wandering in the U.S. Adult General Population, by Ohayon et al., Neurology, Vol. 78, No. 20). Assume that in a random sample of 1480 adults, 455 have sleepwalked.

a. Assuming that the rate of 29.2% is correct, find the probability that 455 or more of the 1480 adults have sleepwalked.

Sleepwalking Assume that 29.2% of people have sleepwalked (based on “Prevalence and Comorbidity of Nocturnal Wandering in the U.S. Adult General Population, by Ohayon et al., Neurology, Vol. 78, No. 20). Assume that in a random sample of 1480 adults, 455 have sleepwalked.

c. What does the result suggest about the rate of 29.2%?

Cell Phones and Brain Cancer In a study of 420,095 cell phone users in Denmark, it was found that 135 developed cancer of the brain or nervous system. For those not using cell phones, there is a 0.000340 probability of a person developing cancer of the brain or nervous system. We therefore expect about 143 cases of such cancers in a group of 420,095 randomly selected people.

a. Find the probability of 135 or fewer cases of such cancers in a group of 420,095 people.

b. What do these results suggest about media reports that suggest cell phones cause cancer of the brain or nervous system?

Overbooking a Boeing 767-300 A Boeing 767-300 aircraft has 213 seats. When someone buys a ticket for a flight, there is a 0.0995 probability that the person will not show up for the flight (based on data from an IBM research paper by Lawrence, Hong, and Cherrier). How many reservations could be accepted for a Boeing 767-300 for there to be at least a 0.95 probability that all reservation holders who show will be accommodated?

Normal Distribution Using a larger data set than the one given for the preceding exercises, assume that cell phone radiation amounts are normally distributed with a mean of 1.17 W/kg and a standard deviation of 0.29 W/kg.

b. Find the value of Q3, the cell phone radiation amount that is the third quartile.

In Exercises 7–10, use the same population of {4, 5, 9} that was used in Examples 2 and 5. As in Examples 2 and 5, assume that samples of size n = 2 are randomly selected with replacement.

Sampling Distribution of the Sample Median

c. Find the mean of the sampling distribution of the sample median.

In Exercises 11–14, use the population of {2, 3, 5, 9} of the lengths of hospital stay (days) of mothers who gave birth, found from Data Set 6 “Births” in Appendix B. Assume that random samples of size n = 2 are selected with replacement.

Sampling Distribution of the Sample Mean

a. After identifying the 16 different possible samples, find the mean of each sample, and then construct a table representing the sampling distribution of the sample mean. In the table, combine values of the sample mean that are the same. (Hint: See Table 6-3 in Example 2.)

Quarters Assume that weights of quarters minted after 1964 are normally distributed with a mean of 5.670 g and a standard deviation of 0.062 g (based on U.S. Mint specifications).

a. Find the probability that a randomly selected quarter weighs between 5.600 g and 5.700 g..

Quarters Assume that weights of quarters minted after 1964 are normally distributed with a mean of 5.670 g and a standard deviation of 0.062 g (based on U.S. Mint specifications).

d. If a vending machine is designed to accept quarters with weights above the 10th percentile P10 find the weight separating acceptable quarters from those that are not acceptable.

Correcting for a Finite Population In a study of babies born with very low birth weights, 275 children were given IQ tests at age 8, and their scores approximated a normal distribution with μ = 95.5 and σ = 16.0 (based on data from “Neurobehavioral Outcomes of School-age Children Born Extremely Low Birth Weight or Very Preterm,” by Anderson et al., Journal of the American Medical Association, Vol. 289, No. 24). Fifty of those children are to be randomly selected without replacement for a follow-up study.

b. Find the probability that the mean IQ score of the follow-up sample is between 95 and 105.

In Exercises 25–28, use these parameters (based on Data Set 1 “Body Data” in Appendix B):

Men’s heights are normally distributed with mean 68.6 in. and standard deviation 2.8 in.

Women’s heights are normally distributed with mean 63.7 in. and standard deviation 2.9 in.

Mickey Mouse Disney World requires that people employed as a Mickey Mouse character must have a height between 56 in. and 62 in.

a. Find the percentage of men meeting the height requirement. What does the result suggest about the genders of the people who are employed as Mickey Mouse characters?

In Exercises 25–28, use these parameters (based on Data Set 1 “Body Data” in Appendix B):

Men’s heights are normally distributed with mean 68.6 in. and standard deviation 2.8 in.

Women’s heights are normally distributed with mean 63.7 in. and standard deviation 2.9 in.

Snow White Disney World requires that women employed as a Snow White character must have a height between 64 in. and 67 in.

a. Find the percentage of women meeting the height requirement.

Designing Helmets Engineers must consider the circumferences of adult heads when designing motorcycle helmets. Adult head circumferences are normally distributed with a mean of 570.0 mm and a standard deviation of 18.3 mm (based on Data Set 3 “ANSUR II 2012”). Due to financial constraints, the helmets will be designed to fit all adults except those with head circumferences that are in the smallest 5% or largest 5%. Find the minimum and maximum head circumferences that the helmets will fit.

Aircraft Seat Width Engineers want to design seats in commercial aircraft so that they are wide enough to fit 99% of all adults. (Accommodating 100% of adults would require very wide seats that would be much too expensive.) Assume adults have hip widths that are normally distributed with a mean of 14.3 in. and a standard deviation of 0.9 in. (based on data from Applied Ergonomics). Find P99. That is, find the hip width for adults that separates the smallest 99% from the largest 1%.

Durations of Pregnancies The lengths of pregnancies are normally distributed with a mean of 268 days and a standard deviation of 15 days.

a. In a letter to “Dear Abby,” a wife claimed to have given birth 308 days after a brief visit from her husband, who was working in another country. Find the probability of a pregnancy lasting 308 days or longer. What does the result suggest?