Identifying the Sample Space of a Probability Experiment In Exercises 25-32, identify the sample space of the probability experiment and determine the number of outcomes in the sample space. Draw a tree diagram when appropriate.

28. Identifying a person's eye color (brown, blue, green, hazel, gray, other) and hair color (black, brown, blonde, red, other).

Identifying the Sample Space of a Probability Experiment In Exercises 25-32, identify the sample space of the probability experiment and determine the number of outcomes in the sample space. Draw a tree diagram when appropriate.

31. Rolling a pair of six-sided dice

Identifying Simple Events In Exercises 33-36, determine the number of outcomes in the event. Then decide whether the event is a simple event or not. Explain your reasoning.

34. A spreadsheet is used to randomly generate a number from 1 to 4000. Event B is generating a number less than 500.

Using the Fundamental Counting Principle In Exercises 37-40, use the Fundamental Counting Principle.

37. Menu A restaurant offers a $15 dinner special that lets you choose from 6 appetizers, 12 entrées, and 8 desserts. How many different meals are available when you select an appetizer, an entrée, and a dessert?

Using the Fundamental Counting Principle In Exercises 37-40, use the Fundamental Counting Principle.

40. True or False Quiz Assuming that no questions are left unanswered, in how many ways can a six-question true or false quiz be answered?

Finding Classical Probabilities In Exercises 41-46, a probability experiment consists of rolling a 12-sided die numbered 1 to 12. Find the probability of the event.

43. Event C: rolling a number greater than 4

Finding Classical Probabilities In Exercises 41-46, a probability experiment consists of rolling a 12-sided die numbered 1 to 12. Find the probability of the event.

46. Event F: rolling a number divisible by 5

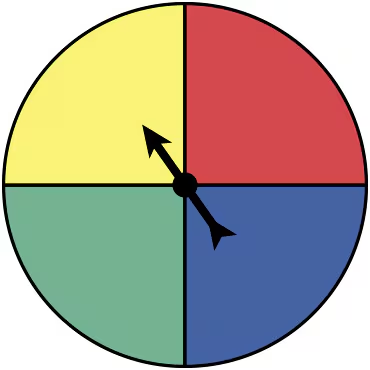
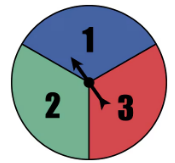
Using a Tree Diagram In Exercises 67-70, a probability experiment consists of rolling a six-sided die and spinning the spinner shown at the left. The spinner is equally likely to land on each color. Use a tree diagram to find the probability of the event. Then explain whether the event can be considered unusual.

68. Event B: rolling an odd number and the spinner landing on green

Boy or Girl? In Exercises 71-74, a couple plans to have three children. Each child is equally likely to be a boy or a girl.

71. What is the probability that all three children are girls?

Boy or Girl? In Exercises 71-74, a couple plans to have three children. Each child is equally likely to be a boy or a girl.

74. What is the probability that at least one child is a boy?

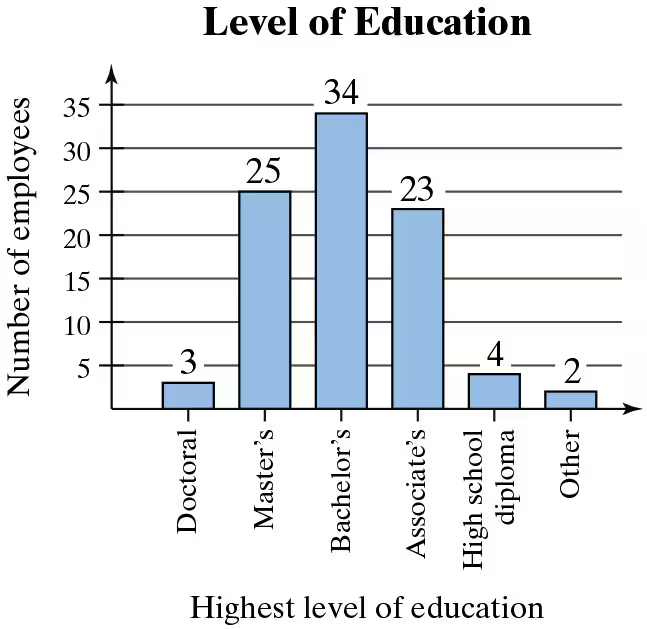
Using a Bar Graph to Find Probabilities In Exercises 75-78, use the bar graph at the left, which shows the highest level of education received by employees of a company. Find the probability that the highest level of education for an employee chosen at random is

77. a master's degree.

80. Unusual Events Can any of the events in Exercises 75-78 be considered unusual? Explain.

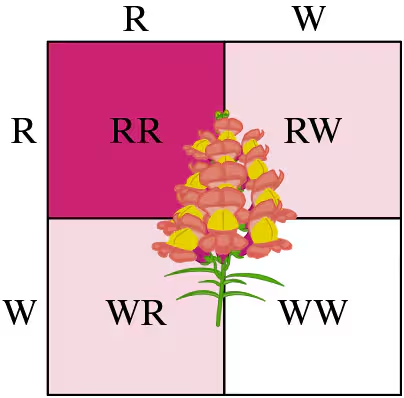
81. Genetics A Punnett square is a diagram that shows all possible gene combinations in a cross of parents whose genes are known. When two pink snapdragon flowers (RW) are crossed, there are four equally likely possible outcomes for the genetic makeup of the offspring: red (RR), pink (RW), pink (WR), and white (WW), as shown in the Punnett square at the left. When two pink snapdragons are crossed, what is the probability that the offspring will be (c) white?

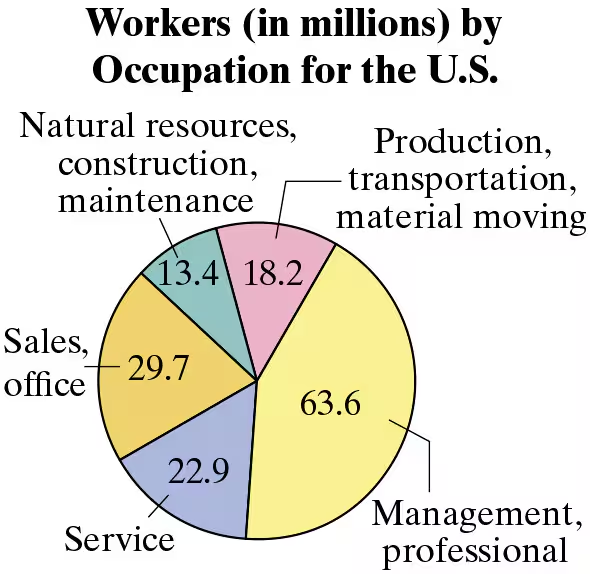
Using a Pie Chart to Find Probabilities In Exercises 83-86, use the pie chart at the left, which shows the number of workers (in millions) by occupation for the United States. (Source: U.S. Bureau of Labor Statistics)

84. Find the probability that a worker chosen at random is not employed in a service occupation.

87. College Football A stem-and-leaf plot for the numbers of touchdowns allowed by the 127 NCAA Division I Football Bowl Subdivision teams in the 2020-2021 season is shown. Find the probability that a team chosen at random allowed (a) at least 51 touchdowns. Are any of these events unusual? Explain. (Source: National Collegiate Athletic Association)

97. Rolling a Pair of Dice You roll a pair of six-sided dice and record the sum.

a. List all of the possible sums and determine the probability of rolling each sum.

b. Use technology to simulate rolling a pair of dice and record the sum 100 times. Make a tally of the 100 sums and use these results to list the probability of rolling

each sum.

c. Compare the probabilities in part (a) with the probabilities in part (b). Explain any similarities or differences.

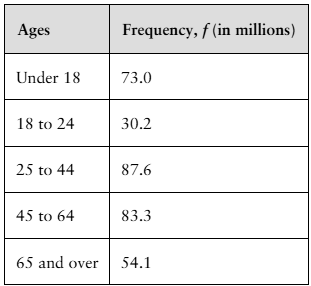
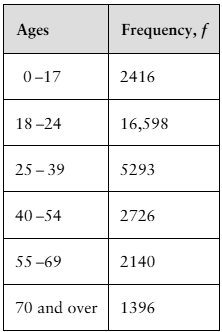
Using a Frequency Distribution to Find Probabilities In Exercises 49-52, use the frequency distribution at the left, which shows the population of the United States by age group, to find the probability that a U.S. resident chosen at random is in the age range. (Source: U.S. Census Bureau)

49. 18 to 24 years old

Using a Frequency Distribution to Find Probabilities In Exercises 49-52, use the frequency distribution at the left, which shows the population of the United States by age group, to find the probability that a U.S. resident chosen at random is in the age range. (Source: U.S. Census Bureau)

52. 65 years old and older

Classifying Types of Probability In Exercises 53-58, classify the statement as an example of classical probability, empirical probability, or subjective probability. Explain your reasoning.

55. An analyst feels that the probability of a team winning an upcoming game is 60%.

Classifying Types of Probability In Exercises 53-58, classify the statement as an example of classical probability, empirical probability, or subjective probability. Explain your reasoning.

58. You estimate that the probability of getting all the classes you want on your next schedule

is about 25%.

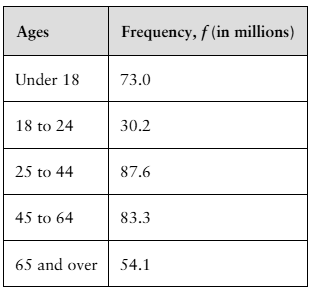
Finding the Probability of the Complement of an Event The age distribution of the residents of Ithaca, New York, is shown at the left. In Exercises 59-62, find the probability of the event. (Source: U.S. Census Bureau)

61. Event C: A randomly chosen resident of Ithaca is not less than 18 years old.

66. Access Code An access code consists of six characters. For each character, any letter or number can be used, with the exceptions that the first character cannot be 0 and the last two characters must be odd numbers.

a. What is the probability of randomly selecting the correct access code on the first try?

88. Individual Stock Price An individual stock is selected at random from the portfolio represented by the box-and-whisker plot shown. Find the probability that the stock price is between $21 and $50.

Writing In Exercises 89 and 90, write a statement that represents the complement of the probability.

90. The probability of randomly choosing a car with more than one cause for showing its "CHECK ENGINE" light from the population of vehicles showing "CHECK ENGINE" lights.

Odds The chances of winning are often written in terms of odds rather than probabilities. The odds of winning is the ratio of the number of successful outcomes to the number of unsuccessful outcomes. The odds of losing is the ratio of the number of unsuccessful outcomes to the number of successful outcomes. For example, when the number of successful outcomes is 2 and the number of unsuccessful outcomes is 3, the odds of winning are 2 : 3 (read "2 to 3"). In Exercises 91-96, use this information about odds.

92. The probability of winning an instant prize game is 1/10. The odds of winning a different instant prize game are 1 : 10. You want the best chance of winning. Which game should you play? Explain your reasoning.

Odds The chances of winning are often written in terms of odds rather than probabilities. The odds of winning is the ratio of the number of successful outcomes to the number of unsuccessful outcomes. The odds of losing is the ratio of the number of unsuccessful outcomes to the number of successful outcomes. For example, when the number of successful outcomes is 2 and the number of unsuccessful outcomes is 3, the odds of winning are 2 : 3 (read "2 to 3"). In Exercises 91-96, use this information about odds.

94. A card is picked at random from a standard deck of 52 playing cards. Find the odds that it is a spade.

"Identifying the Sample Space of a Probability Experiment In Exercises 25-32, identify the sample space of the probability experiment and determine the number of outcomes in the sample space. Draw a tree diagram when appropriate.

26. Guessing a student's letter grade (A, B, C, D, F) in a class

"

Identifying the Sample Space of a Probability Experiment In Exercises 25-32, identify the sample space of the probability experiment and determine the number of outcomes in the sample space. Draw a tree diagram when appropriate.

32. Rolling a six-sided die, tossing two coins, and spinning the fair spinner shown

"Identifying Simple Events In Exercises 33-36, determine the number of outcomes in the event. Then decide whether the event is a simple event or not. Explain your reasoning.

36. You randomly select one card from a standard deck of 52 playing cards. Event B is selecting the ace of spades."

According to Bayes’ Theorem, the probability of event A , given that event B has occurred, is

P(A|B) = P(A) * P(B|A)P(A) * P(B|A) + P(A') * P(B|A').

In Exercises 33–38, use Bayes’ Theorem to find P(A|B).

33. P(A) = 2/3, P(A') = 1/3, P(B|A) = 1/5 , and P(B|A') = 1/2