Back
BackProblem 3.RS.2a
You work in the security department of a bank’s website. To access their accounts, customers of the bank must create an 8-digit password. It is your job to determine the password requirements for these accounts. Security guidelines state that for the website to be secure, the probability that an 8-digit password is guessed on one try must be less than 1/60^8, assuming all passwords are equally likely.
Your job is to use the probability techniques you have learned in this chapter to decide what requirements a customer must meet when choosing a password, including what sets of characters are allowed, so that the website is secure according to the security guidelines.
2. Answering the Question
a. What password requirements would you set? What characters would be allowed?
Problem 3.RS.3b
You work in the security department of a bank’s website. To access their accounts, customers of the bank must create an 8-digit password. It is your job to determine the password requirements for these accounts. Security guidelines state that for the website to be secure, the probability that an 8-digit password is guessed on one try must be less than 1/60^8, assuming all passwords are equally likely.
Your job is to use the probability techniques you have learned in this chapter to decide what requirements a customer must meet when choosing a password, including what sets of characters are allowed, so that the website is secure according to the security guidelines.
3. For additional security, each customer creates a 5-digit PIN (personal identification number). The table on the right shows the 10 most commonly chosen 5-digit PINs. From the table, you can see that more than a third of all 5-digit PINs could be guessed by trying these 10 numbers. To discourage customers from using predictable PINs, you consider prohibiting PINs that use the same digit more than once.
b. Would you decide to prohibit PINs that use the same digit more than once? Explain.
Problem 3.T.2
2. How many possible variations are there in Mozart's Musical Dice Game minuet? Explain.
Problem 3.T.5
5. Use technology to randomly select two numbers from 1 to 6. Find the sum and subtract 1 to obtain a total.
a. What is the theoretical probability of each total from 1 to 11?
b. Use this procedure to select 100 totals from 1 to 11. Tally your results and compare them with the probabilities in part (a).
Problem 3.RE.42
In Exercises 41-44, perform the indicated calculation.
42. 8P6
Problem 3.RE.44
In Exercises 41-44, perform the indicated calculation.
44. (5C3)/(10C3)
Problem 3.T.4a
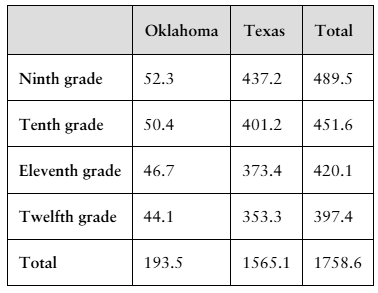
4. The table on the left shows the secondary school student enrollment levels (in thousands by grade) in Oklahoma and Texas schools in a recent year. (Source: U.S. Nation
for Education Statistics)
A student in one of the indicated grades and states is randomly selected. Find the probability of selecting a student who
a. is in ninth grade.
Problem 3.T.4d
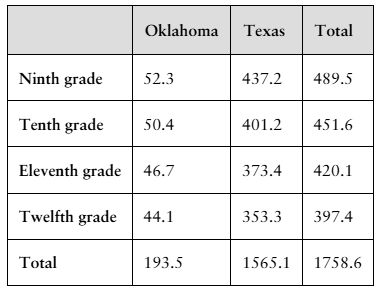
4. The table on the left shows the secondary school student enrollment levels (in thousands by grade) in Oklahoma and Texas schools in a recent year. (Source: U.S. Nation
for Education Statistics)
A student in one of the indicated grades and states is randomly selected. Find the probability of selecting a student who
d. is enrolled in Texas, given that the student is in twelfth grade.
Problem 3.Test.5
5. Which event(s) in Exercise 4 can be considered unusual? Explain your reasoning.
Problem 3.T.7b
7. There are 16 students giving final presentations in your history course.
b. Presentation subjects are based on the units of the course. Unit B is covered by three students, Unit C is covered by five students, and Units A and D are each covered by four students. How many presentation orders are possible when presentations on
the same unit are indistinguishable from each other?
Problem 3.R.1
"In Exercises 1-4, identify the sample space of the probability experiment and determine the number of outcomes in the event. Draw a tree diagram when appropriate.
1. Experiment: Tossing four coins
Event: Getting three heads"
Problem 3.R.4
"In Exercises 1-4, identify the sample space of the probability experiment and determine the number of outcomes in the event. Draw a tree diagram when appropriate.
4. Experiment: Guessing the gender(s) of the three children in a family
Event: Guessing that the family has two boys"
Problem 3.R.5
"In Exercises 5 and 6, use the Fundamental Counting Principle.
5. A student must choose from seven classes to take at 8:00 A.M., four classes to take at 9:00 A.M., and three classes to take at 10:00 A.M. How many ways can the student arrange the schedule?"
Problem 3.RE.20
"In Exercises 19-22, determine whether the events are independent or dependent. Explain your reasoning.
20. Selecting an ace from a standard deck of 52 playing cards, and then selecting a jack from the deck without replacing the ace"
Problem 3.RE.21
"In Exercises 19-22, determine whether the events are independent or dependent. Explain your reasoning.
21. Taking a driver's education course and passing the driver's license exam"
Problem 3.R.17
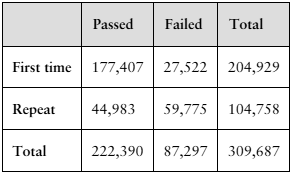
In Exercises 17 and 18, use the table, which shows the numbers of first-time and repeat U.S. nursing students taking the National Council Licensure Examination (NCLEX-RN® exam) to pass or fail in a recent year. (Adapted from National Council Licensure Examinations)
17. Find the probability that a student took the exam for the first time, given that the student failed.
Problem 3.R.18
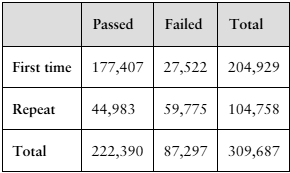
"In Exercises 17 and 18, use the table, which shows the numbers of first-time and repeat U.S. nursing students taking the National Council Licensure Examination (NCLEX-RN® exam) to pass or fail in a recent year. (Adapted from National Council Licensure Examinations)
18. Find the probability that a student passed, given that the student repeated the exam."
Problem 3.1.2a
2. Determine whether each number could represent the probability of an event. Explain your reasoning. a. 25/25
Problem 3.1.2b
2. Determine whether each number could represent the probability of an event. Explain your reasoning. b. 333.3%
Problem 3.1.2c
2. Determine whether each number could represent the probability of an event. Explain your reasoning. c. 2.3
Problem 3.1.2d
2. Determine whether each number could represent the probability of an event. Explain your reasoning. d. -0.0004
Problem 3.1.3
3. Explain why the statement is incorrect: The probability of rain is 150%.
Problem 3.1.9
True or False? In Exercises 7-10, determine whether the statement is true or false. If it is false, rewrite it as a true statement.
9. A probability of 1/10 indicates an unusual event.
Problem 3.1.11
Matching Probabilities In Exercises 11-16, match the event with its probability.
a. 0.95
b. 0.005
c. 0.25
d. 0
e. 0.375
f. 0.5
11. A random number generator is used to select a number from 1 to 100. What is the probability of selecting the number 153?
Problem 3.1.14
Matching Probabilities In Exercises 11-16, match the event with its probability.
a. 0.95
b. 0.005
c. 0.25
d. 0
e. 0.375
f. 0.5
14. A game show contestant must randomly select a door. One door doubles her money while the other three doors leave her with no winnings. What is the probability she selects the
door that doubles her money?
Problem 3.1.16
Matching Probabilities In Exercises 11-16, match the event with its probability.
a. 0.95
b. 0.005
c. 0.25
d. 0
e. 0.375
f. 0.5
16. You toss a coin four times. What is the probability of tossing tails exactly half of the time?
Problem 3.1.19
Finding the Probability of the Complement of an Event In Exercises 17-20, the probability that an event will happen is given. Find the probability that the event will not happen.
19. P(E)=0.03
Problem 3.1.21
Finding the Probability of an Event In Exercises 21-24, the probability that an event will not happen is given. Find the probability that the event will happen.
21. P(E') =0.95
Problem 3.1.23
Finding the Probability of an Event In Exercises 21-24, the probability that an event will not happen is given. Find the probability that the event will happen.
23. P(E')=3/4
Problem 3.1.25
Identifying the Sample Space of a Probability Experiment In Exercises 25-32, identify the sample space of the probability experiment and determine the number of outcomes in the sample space. Draw a tree diagram when appropriate.
25. Guessing the initial of a student's middle name