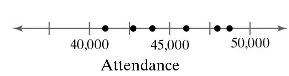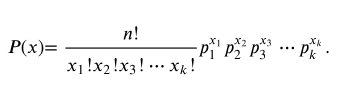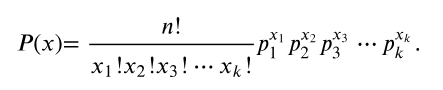Larson - Elementary Statistics: Picturing the World 8th Edition

Ch. 4 - Discrete Probability Distributions

Back

All textbooks

Larson 8th Edition

Ch. 4 - Discrete Probability Distributions

Problem 4.3.30

Geometric Distribution: Mean and Variance In Exercises 29 and 30, use the fact that the mean of a geometric distribution is μ = 1/p and the variance is

sigma^2 = q/p^2

Paycheck Errors A company assumes that 0.5% of the paychecks for a year were calculated incorrectly. The company has 200 employees and examines the payroll records from one month. (a) Find the mean, variance, and standard deviation. (b) How many employee payroll records would you expect to examine before finding one with an error?

Problem 4.1.40

Baseball There were 116 World Series from 1903 to 2020. Use the probability distribution in Exercise 30 to find the number of World Series that had 4, 5, 6, 7, and 8 games. Find the population mean, variance, and standard deviation of the data using the traditional definitions. Compare to your answers in Exercise 30.

Problem 4.1.25

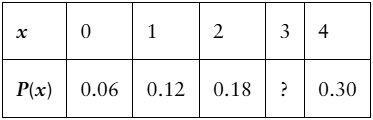
Determining a Missing Probability In Exercises 25 and 26, determine the missing probability for the probability distribution.

Problem 4.1.9

Graphical Analysis In Exercises 9–12, determine whether the graph on the number line represents a discrete random variable or a continuous random variable. Explain your reasoning.

The attendance at concerts for a rock group

Problem 4.2.33

Finding and Interpreting Mean, Variance, and Standard Deviation In Exercises 31–36, find the mean, variance, and standard deviation of the binomial distribution for the given random variable. Interpret the results and determine any unusual values.

Life on Other Planets Seventy-nine percent of U.S. adults believe that life on other planets is plausible. You randomly select eight U.S. adults and ask them whether they believe that life on other planets is plausible. The random variable represents the number who believe that life on other planets is plausible. (Source: Ipsos)

Problem 4.2.35

Late for Work Thirty-one percent of U.S. employees who are late for work blame oversleeping. You randomly select 12 U.S. employees who are late for work and ask them whether they blame oversleeping. The random variable represents the number who are late for work and blame oversleeping. (Source: CareerBuilder)

Problem 4.2.18

Identifying and Understanding Binomial Experiments In Exercises 15–18, determine whether the experiment is a binomial experiment. If it is, identify a success; specify the values of n, p, and q; and list the possible values of the random variable x. If it is not a binomial experiment, explain why.

Basketball A’ja Wilson, the 2020 WNBA Most Valuable Player, makes a free throw shot about 78% of the time. The random variable represents the number of free throws that she makes on eight attempts. (Source: Women’s National Basketball Association)

Problem 4.3.1

In Exercises 1– 4, find the indicated probability using the geometric distribution.

Find P(3) when p = 0.65

Problem 4.3.3

In Exercises 1– 4, find the indicated probability using the geometric distribution.

Find P(5) when p = 0.09

Problem 4.1.27

Identifying Probability Distributions In Exercises 27 and 28, determine whether the distribution is a probability distribution. If it is not a probability distribution, explain why.

Problem 4.2.22

Finding Binomial Probabilities In Exercises 19–26, find the indicated probabilities. If convenient, use technology or Table 2 in Appendix B.

Penalty Kicks Argentine soccer player Lionel Messi converts 78% of his penalty kicks. Suppose Messi takes six penalty kicks next season. Find the probability that the number he converts is (a) exactly six, (b) at most three, and (c) more than three. (Source: Transfermarkt)

Problem 4.3.10

In your own words, describe the difference between the value of x in a binomial distribution and in the Poisson distribution.

Problem 4.3.13

"Using a Distribution to Find Probabilities In Exercises 11–26, find the indicated probabilities using the geometric distribution, the Poisson distribution, or the binomial distribution. Then determine whether the events are unusual. If convenient, use a table or technology to find the probabilities.

Typographical Errors A newspaper finds that the mean number of typographical errors per page is four. Find the probability that the number of typographical errors found on any given page is (a) exactly three, (b) at most three, and (c) more than three."

Problem 4.2.39

Multinomial Experiments In Exercises 39 and 40, use the information below.

A multinomial experiment satisfies these conditions.

The experiment has a fixed number of trials n, where each trial is independent of the other trials.

Each trial has k possible mutually exclusive outcomes:

Each outcome has a fixed probability. So, . The sum of the probabilities for all outcomes is

The number of times occurs is , the number of times occurs is , the number of times occurs is , and so on.

The discrete random variable x counts the number of times that each outcome occurs in n independent trials where . The probability that x will occur is

Genetics According to a theory in genetics, when tall and colorful plants are crossed with short and colorless plants, four types of plants will result: tall and colorful, tall and colorless, short and colorful, and short and colorless, with corresponding probabilities of , and . Ten plants are selected. Find the probability that 5 will be tall and colorful, 2 will be tall and colorless, 2 will be short and colorful, and 1 will be short and colorless.

Problem 4.3.12

Using a Distribution to Find Probabilities In Exercises 11–26, find the indicated probabilities using the geometric distribution, the Poisson distribution, or the binomial distribution. Then determine whether the events are unusual. If convenient, use a table or technology to find the probabilities.

Immigration The mean number of people who immigrated to the United States per hour was about 5.5 in April 2021. Find the probability that the number of people who immigrate to the U.S. in a given hour in April 2021 was (a) zero, (b) exactly five, and (c) exactly eight. (Source: U.S. Census Bureau)

Problem 4.2.15

Video Games A survey found that 29% of gamers own a virtual reality (VR) device. Ten gamers are randomly selected. The random variable represents the number who own a VR device. (Source: Entertainment Software Association)

Problem 4.1.38

Finding an Expected Value In Exercises 37 and 38, find the expected value E(x) to the player for one play of the game. If x is the gain to a player in a game of chance, then E(x) is usually negative. This value gives the average amount per game the player can expect to lose.

A high school basketball team is selling $10 raffle tickets as part of a fund-raising program. The first prize is a trip to the Bahamas valued at $5460, and the second prize is a weekend ski package valued at $496. The remaining 18 prizes are $100 gas cards. The number of tickets sold is 3500.

Problem 4.2.27

Constructing and Graphing Binomial Distributions In Exercises 27–30, (a) construct a binomial distribution, (b) graph the binomial distribution using a histogram and describe its shape, and (c) identify any values of the random variable x that you would consider unusual. Explain your reasoning.

College Acceptance Pennsylvania State University accepts 49% of applicants. You randomly select seven Pennsylvania State University applicants. The random variable represents the number who are accepted. (Source: US News & World Report)

Problem 4.1.17

Discrete Variables and Continuous Variables In Exercises 13–18, determine whether the random variable x is discrete or continuous. Explain.

Let x represent the fitted hat sizes of members of a softball team.

Problem 4.1.6

True or False? In Exercises 5–8, determine whether the statement is true or false. If it is false, rewrite it as a true statement.

For a random variable x, the word random indicates that the value of x is determined by chance.

Problem 4.1.19

Constructing and Graphing Discrete Probability Distributions In Exercises 19 and 20, (a) construct a probability distribution, and (b) graph the probability distribution using a histogram and describe its shape.

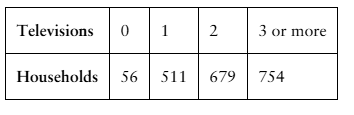
Televisions The number of high-definition (HD) televisions per household in a small town

Problem 4.2.14

Mean, Variance, and Standard Deviation In Exercises 11–14, find the mean, variance, and standard deviation of the binomial distribution with the given values of n and p.

n = 316, p = 0.82

Problem 4.1.41

Linear Transformation of a Random Variable In Exercises 41 and 42, use this information about linear transformations. For a random variable x, a new random variable y can be created by applying a linear transformation , where a and b are constants. If the random variable x has mean and standard deviation , then the mean, variance, and standard deviation of y are given by the formulas

The mean annual salary of employees at an office is originally $46,000. Each employee receives an annual bonus of $600 and a 3% raise (based on salary). What is the new mean annual salary (including the bonus and raise)?

Problem 4.2.40

"Multinomial Experiments In Exercises 39 and 40, use the information below.

A multinomial experiment satisfies these conditions.

The experiment has a fixed number of trials n, where each trial is independent of the other trials.

Each trial has k possible mutually exclusive outcomes:

Each outcome has a fixed probability. So, . The sum of the probabilities for all outcomes is

The number of times occurs is , the number of times occurs is , the number of times occurs is , and so on.

The discrete random variable x counts the number of times that each outcome occurs in n independent trials where . The probability that x will occur is

Genetics Another proposed theory in genetics gives the corresponding probabilities for the four types of plants described in Exercise 39 as , and . Ten plants are selected. Find the probability that 5 will be tall and colorful, 2 will be tall and colorless, 2 will be short and colorful, and 1 will be short and colorless."

Problem 4.3.6

In Exercises 5–8, find the indicated probability using the Poisson distribution.

P(3) when μ = 6

Problem 4.1.29

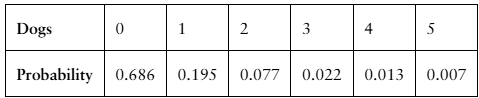
Finding the Mean, Variance, and Standard Deviation In Exercises 29–34, (a) find the mean, variance, and standard deviation of the probability distribution, and (b) interpret the results.

Dogs The number of dogs per household in a neighborhood

Problem 4.2.30

Workplace Cleanliness Fifty-seven percent of employees judge their peers by the cleanliness of their workspaces. You randomly select 10 employees and ask them whether they judge their peers by the cleanliness of their workspaces. The random variable represents the number who judge their peers by the cleanliness of their workspaces. (Source: Adecco)

Problem 4.3.15

Pass Completions NFL player Aaron Rodgers completes a pass 65.1% of the time. Find the probability that (a) the first pass he completes is the second pass, (b) the first pass he completes is the first or second pass, and (c) he does not complete his first two passes. (Source: National Football League)

Problem 4.1.43

Independent and Dependent Random Variables Two random variables x and y are independent when the value of x does not affect the value of y. When the variables are not independent, they are dependent. A new random variable can be formed by finding the sum or difference of random variables. If a random variable x has mean and a random variable y has mean , then the means of the sum and difference of the variables are given by . If random variables are independent, then the variance and standard deviation of the sum or difference of the random variables can be found. So, if a random variable x has variance and a random variable y has variance , then the variances of the sum and difference of the variables are given by In Exercises 43 and 44, the distribution of SAT mathematics scores for college-bound male seniors in 2020 has a mean of 531 and a standard deviation of 121. The distribution of SAT mathematics scores for college-bound female seniors in 2020 has a mean of 516 and a standard deviation of 112. One male and one female are randomly selected. Assume their scores are independent. (Adapted from College Board)

Find the mean and standard deviation of the sum of their scores.

Problem 4.1.23

Unusual Events In Exercise 19, would it be unusual for a household to have no HD televisions? Explain your reasoning.