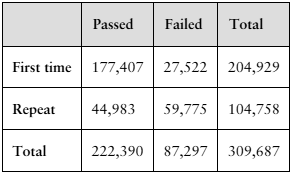
"In Exercises 17 and 18, use the table, which shows the numbers of first-time and repeat U.S. nursing students taking the National Council Licensure Examination (NCLEX-RN® exam) to pass or fail in a recent year. (Adapted from National Council Licensure Examinations)

18. Find the probability that a student passed, given that the student repeated the exam."

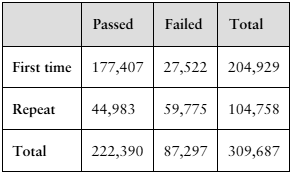
In Exercises 17 and 18, use the table, which shows the numbers of first-time and repeat U.S. nursing students taking the National Council Licensure Examination (NCLEX-RN® exam) to pass or fail in a recent year. (Adapted from National Council Licensure Examinations)

17. Find the probability that a student took the exam for the first time, given that the student failed.

"In Exercises 1-4, identify the sample space of the probability experiment and determine the number of outcomes in the event. Draw a tree diagram when appropriate.

1. Experiment: Tossing four coins

Event: Getting three heads"

In Exercises 49-53, use counting principles to find the probability.

53. A corporation has six male senior executives and four female senior executives. Four senior executives are chosen at random to attend a technology seminar. What is the

probability of choosing

b. four women?

In Exercises 49-53, use counting principles to find the probability.

53. A corporation has six male senior executives and four female senior executives. Four senior executives are chosen at random to attend a technology seminar. What is the

probability of choosing

c. two men and two women?

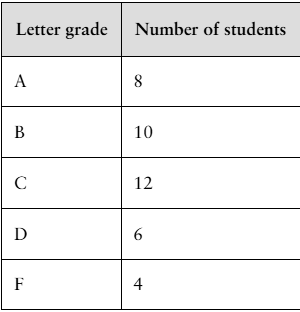
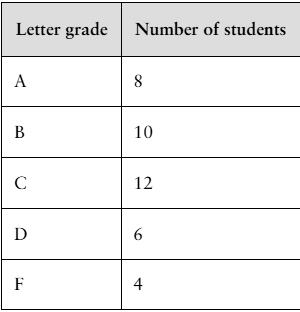
In Exercises 49-53, use counting principles to find the probability.

52. A class of 40 students takes a statistics exam. The results are shown in the table at the left. Three students are selected at random. What is the probability that

b. all three students received a C or better?

In Exercises 49-53, use counting principles to find the probability.

51. A shipment of 200 calculators contains 3 defective units. What is the probability that a sample of three calculators will have

c. at least one defective calculator?

In Exercises 49-53, use counting principles to find the probability.

50. A security code consists of three letters and one digit. The first letter cannot be A, B, or C. What is the probability of guessing the security code on the first try?

"In Exercises 5 and 6, use the Fundamental Counting Principle.

5. A student must choose from seven classes to take at 8:00 A.M., four classes to take at 9:00 A.M., and three classes to take at 10:00 A.M. How many ways can the student arrange the schedule?"

In Exercises 49-53, use counting principles to find the probability.

52. A class of 40 students takes a statistics exam. The results are shown in the table at the left. Three students are selected at random. What is the probability that

d. all three students received a B or a C?

"In Exercises 1-4, identify the sample space of the probability experiment and determine the number of outcomes in the event. Draw a tree diagram when appropriate.

4. Experiment: Guessing the gender(s) of the three children in a family

Event: Guessing that the family has two boys"

In Exercises 45-48, use combinations and permutations.

46. Five players on a basketball team must each choose one of the five players on the opposing team to defend. In how many ways can the players choose their defensive assignments?

Telephone Numbers The telephone numbers for a region of Pennsylvania have an area code of 570. The next seven digits represent the local telephone numbers for that region. These cannot begin with a 0 or 1. In Exercises 15 and 16, assume your cousin lives within the given area code.

16. What is the probability of not randomly generating your cousin's telephone number on the first try?

In Exercises 41-44, perform the indicated calculation.

44. (5C3)/(10C3)

In Exercises 1-4, identify the sample space of the probability experiment and determine the number of outcomes in the event. Draw a tree diagram when appropriate.

3. Experiment: Choosing a month of the year

Event: Choosing a month that begins with the letter J

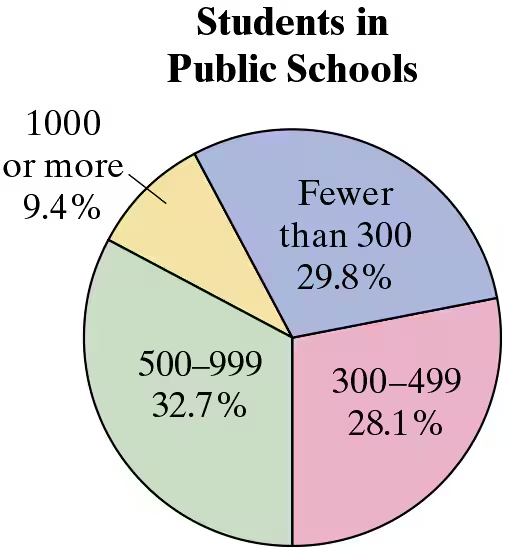
In Exercises 33 and 34, use the pie chart at the left, which shows the percent distribution of the number of students in U.S. public schools in a recent year. (Source: U.S. National Center for Education Statistics)

34. Find the probability of randomly selecting a school with 300 or more students.

In Exercises 19-22, determine whether the events are independent or dependent. Explain your reasoning.

22. Getting high grades and being awarded an academic scholarship

In Exercises 19-22, determine whether the events are independent or dependent. Explain your reasoning.

19. Tossing a coin four times and getting four heads, and then tossing it a fifth time and getting a head

"In Exercises 19-22, determine whether the events are independent or dependent. Explain your reasoning.

20. Selecting an ace from a standard deck of 52 playing cards, and then selecting a jack from the deck without replacing the ace"

28. A sample of 6500 automobiles found that 1560 of the automobiles were black, 3120 of the automobiles were sedans, and 1170 of the automobiles were black sedans. Find the probability that a randomly chosen automobile from this sample is black or a sedan.

In Exercises 41-44, perform the indicated calculation.

42. 8P6

In Exercises 5 and 6, use the Fundamental Counting Principle.

6. The state of Virginia's license plates have three letters and four digits. Assuming that any letter or digit can be used, how many different license plates are possible?

In Exercises 25 and 26, determine whether the events are mutually exclusive. Explain your reasoning.

25. Event A: Randomly select a red jelly bean from a jar.

Event B: Randomly select a yellow jelly bean from the jar.

In Exercises 7-12, classify the statement as an example of classical probability, empirical probability, or subjective probability. Explain your reasoning.

8. The probability of randomly selecting five cards of the same suit from a standard deck of 52 playing cards is about 0.002.

In Exercises 13 and 14, use the table, which shows the approximate distribution of the sizes of firms for a recent year. (Adapted from North American Industry Classification System)

13. Find the probability that a randomly selected firm will have more than four employees.

"In Exercises 19-22, determine whether the events are independent or dependent. Explain your reasoning.

21. Taking a driver's education course and passing the driver's license exam"

In Exercises 7-12, classify the statement as an example of classical probability, empirical probability, or subjective probability. Explain your reasoning.

11. The probability of rolling 2 six-sided dice and getting a sum of 9 is 1/9.

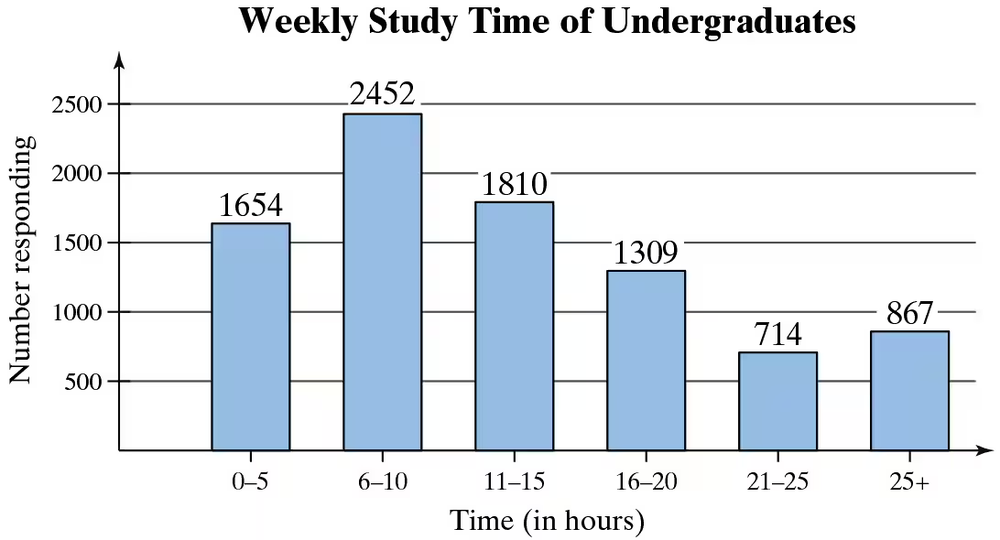
In Exercises 35–38, the bar graph shows the results of a survey in which 8806 undergraduate students were asked how many hours they spend on studying and other academic activities outside of class in a typical week. (Source: American College Health Association)

37. Find the probability of randomly selecting an undergraduate who does not study from 6 to 10 hours per week.

In Exercises 29-32, find the probability.

31. A 12-sided die, numbered 1 to 12, is rolled. Find the probability that the roll results in an odd number or a number less than 4.

39. You are given that P(A) = 0.15 and P(B) = 0.40. Do you have enough information to find P(A or B)? Explain.