Cards In Exercises 59-62, you are dealt a hand of five cards from a standard deck of 52 playing cards.

62. Find the probability of being dealt three of a kind (the other two cards are different from each other).

Classifying Events Based on Studies In Exercises 15-18, identify the two events described in the study. Do the results indicate that the events are independent or dependent? Explain your reasoning.

17. A study found that there is no relationship between playing violent video games and aggressive or bullying behavior in teenagers. (Source: The Royal Society Publishing)

True or False? In Exercises 3-6, determine whether the statement is true or false. If it is false, rewrite it as a true statement.

3. A combination is an ordered arrangement of objects.

Odds The chances of winning are often written in terms of odds rather than probabilities. The odds of winning is the ratio of the number of successful outcomes to the number of unsuccessful outcomes. The odds of losing is the ratio of the number of unsuccessful outcomes to the number of successful outcomes. For example, when the number of successful outcomes is 2 and the number of unsuccessful outcomes is 3, the odds of winning are 2 : 3 (read "2 to 3"). In Exercises 91-96, use this information about odds.

94. A card is picked at random from a standard deck of 52 playing cards. Find the odds that it is a spade.

"According to Bayes’ Theorem, the probability of event A , given that event B has occurred, is

P(A|B) = P(A) * P(B|A)P(A) * P(B|A) + P(A') * P(B|A').

In Exercises 33–38, use Bayes’ Theorem to find P(A|B).

35. P(A) = 0.25, P(A') = 0.75, P(B|A) = 0.3 , and P(B|A') = 0.5 "

Using the Fundamental Counting Principle In Exercises 37-40, use the Fundamental Counting Principle.

37. Menu A restaurant offers a $15 dinner special that lets you choose from 6 appetizers, 12 entrées, and 8 desserts. How many different meals are available when you select an appetizer, an entrée, and a dessert?

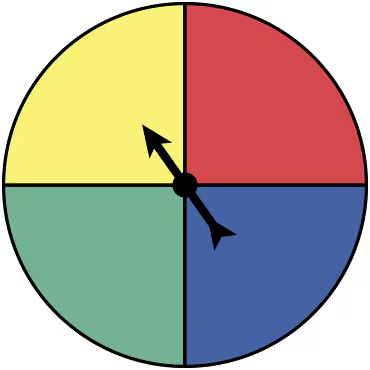
Using a Tree Diagram In Exercises 67-70, a probability experiment consists of rolling a six-sided die and spinning the spinner shown at the left. The spinner is equally likely to land on each color. Use a tree diagram to find the probability of the event. Then explain whether the event can be considered unusual.

68. Event B: rolling an odd number and the spinner landing on green

In Exercises 15-18, determine whether the situation involves permutations, combinations, or neither. Explain your reasoning.

15. The number of ways 16 floats can line up in a row for a parade

3. Explain why the statement is incorrect: The probability of rain is 150%.

1. When two events are mutually exclusive, why is P(A and B) = 0?

Using the Multiplication Rule In Exercises 19-32, use the Multiplication Rule.

20. Coin and Die A coin is tossed and a die is rolled. Find the probability of tossing a tail and then rolling a number greater than 2.

Finding the Probability of an Event In Exercises 21-24, the probability that an event will not happen is given. Find the probability that the event will happen. 

23. P(E')=3/4

Matching Probabilities In Exercises 11-16, match the event with its probability.

a. 0.95

b. 0.005

c. 0.25

d. 0

e. 0.375

f. 0.5

11. A random number generator is used to select a number from 1 to 100. What is the probability of selecting the number 153?

Identifying Simple Events In Exercises 33-36, determine the number of outcomes in the event. Then decide whether the event is a simple event or not. Explain your reasoning.

34. A spreadsheet is used to randomly generate a number from 1 to 4000. Event B is generating a number less than 500.

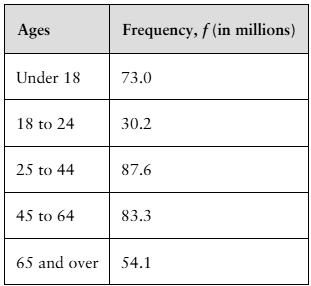
Using a Frequency Distribution to Find Probabilities In Exercises 49-52, use the frequency distribution at the left, which shows the population of the United States by age group, to find the probability that a U.S. resident chosen at random is in the age range. (Source: U.S. Census Bureau)

49. 18 to 24 years old

Identifying the Sample Space of a Probability Experiment In Exercises 25-32, identify the sample space of the probability experiment and determine the number of outcomes in the sample space. Draw a tree diagram when appropriate.

31. Rolling a pair of six-sided dice

31. Experiment A researcher is randomly selecting a treatment group of 10 human subjects from a group of 20 people taking part in an experiment. In how many different ways can the treatment group be selected?

"True or False? In Exercises 5 and 6, determine whether the statement is true or false. If it is false, rewrite it as a true statement.

5. If two events are independent, then P(A|B) = P(B)."

"Classifying Events as Independent or Dependent In Exercises 9-14, determine whether the events are independent or dependent. Explain your reasoning.

10. A father having hazel eyes and a daughter having hazel eyes"

Finding Classical Probabilities In Exercises 41-46, a probability experiment consists of rolling a 12-sided die numbered 1 to 12. Find the probability of the event.

43. Event C: rolling a number greater than 4

Identifying the Sample Space of a Probability Experiment In Exercises 25-32, identify the sample space of the probability experiment and determine the number of outcomes in the sample space. Draw a tree diagram when appropriate.

28. Identifying a person's eye color (brown, blue, green, hazel, gray, other) and hair color (black, brown, blonde, red, other).

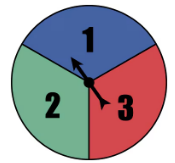
Identifying the Sample Space of a Probability Experiment In Exercises 25-32, identify the sample space of the probability experiment and determine the number of outcomes in the sample space. Draw a tree diagram when appropriate.

32. Rolling a six-sided die, tossing two coins, and spinning the fair spinner shown

In Exercises 15-18, determine whether the situation involves permutations, combinations, or neither. Explain your reasoning.

17. The number of ways 2 captains can be chosen from 28 players on a lacrosse team

According to Bayes’ Theorem, the probability of event A , given that event B has occurred, is

P(A|B) = P(A) * P(B|A)P(A) * P(B|A) + P(A') * P(B|A').

In Exercises 33–38, use Bayes’ Theorem to find P(A|B).

33. P(A) = 2/3, P(A') = 1/3, P(B|A) = 1/5 , and P(B|A') = 1/2

"According to Bayes’ Theorem, the probability of event A , given that event B has occurred, is

P(A|B) = P(A) * P(B|A)P(A) * P(B|A) + P(A') * P(B|A').

In Exercises 33–38, use Bayes’ Theorem to find P(A|B).

36. P(A) = 0.62, P(A') = 0.38, P(B|A) = 0.41 , and P(B|A') = 0.17 "

34. Lottery Number Selection A lottery has 52 numbers. In how many different ways can six of the numbers be selected? (Assume the order of selection is not important.)

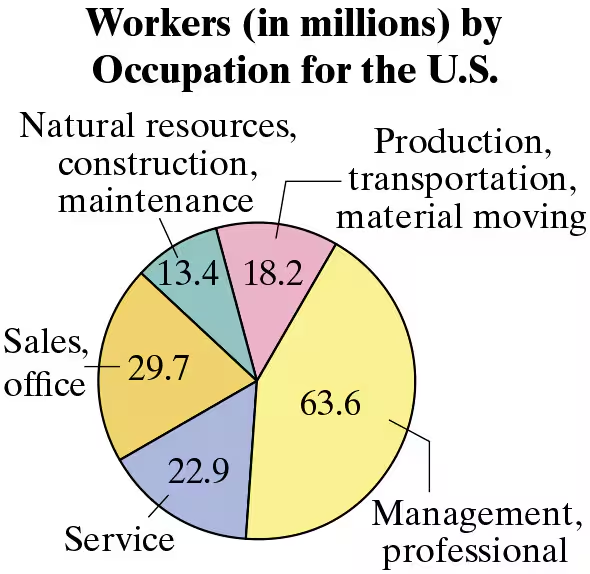
Using a Pie Chart to Find Probabilities In Exercises 83-86, use the pie chart at the left, which shows the number of workers (in millions) by occupation for the United States. (Source: U.S. Bureau of Labor Statistics)

84. Find the probability that a worker chosen at random is not employed in a service occupation.

In Exercises 7-14, perform the indicated calculation.

9.8C3

56. Defective Disks A pack of 100 recordable DVDs contains 5 defective disks. You select four disks. What is the probability of selecting at least three non defective disks?

Cards In Exercises 59-62, you are dealt a hand of five cards from a standard deck of 52 playing cards.

59. Find the probability of being dealt two clubs and one of each of the other three suits.