Back
BackProblem 1.CR.2
In Exercises 1 and 2, identify the sampling technique used, and discuss potential sources of bias (if any). Explain.
Using random digit dialing, researchers asked 1090 U.S. adults their level of education.
Problem 2.R.43
A student’s test grade of 75 represents the 65th percentile of the grades. What percent of students scored higher than 75?
Problem 2.R.17
In Exercises 17–19, use the data set, which represents the points recorded by each player on the Winnipeg Jets in the 2019–2020 NHL season. (Source: National Hockey League)
8 8 8 6 0 73 26 1
0 5 58 1 7 5 10 63
0 5 10 0 31 5 15 45
16 29 10 73 5 3 0 65
Construct a frequency distribution for the data set using eight classes. Include class limits, midpoints, boundaries, frequencies, relative frequencies, and cumulative frequencies.
Problem 2.Q.1a
The data set represents the number of minutes a sample of 27 people exercise each week.
108 139 120 123 120 132 123 131 131
157 150 124 111 101 135 119 116 117
127 128 139 119 118 114 127 142 130
a. Construct a frequency distribution for the data set using five classes. Include class limits, midpoints, boundaries, frequencies, relative frequencies, and cumulative frequencies.
Problem 2.RE.5
In Exercises 5 and 6, use the data set, which represents the number of rooms reserved during one night’s business at a sample of hotels.
153 104 118 166 89 104 100 79 93 96 116
94 140 84 81 96 108 111 87 126 101 111
122 108 126 93 108 87 103 95 129 93 124
Construct a frequency distribution for the data set with six classes and draw a frequency polygon.
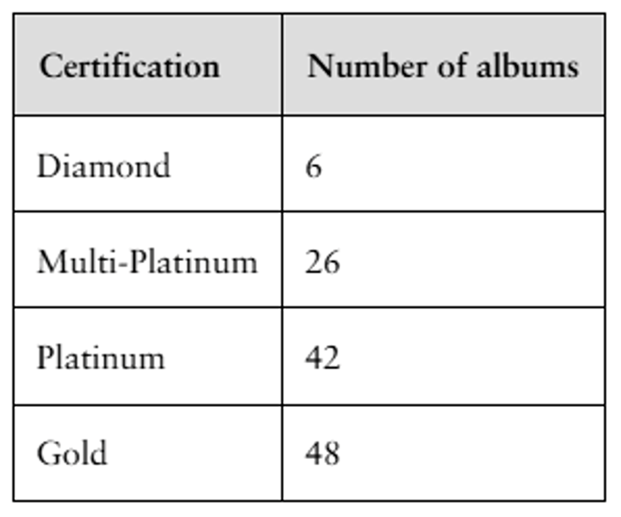
Problem 2.T.5b
The table lists the number of albums by The Beatles that received sales certifications. Display the data using (b) a Pareto chart. (Source: Recording Industry Association of America)
Problem 2.T.6
The number of minutes it took 12 students in a statistics class to complete the final exam are listed. Use a scatter plot to display this data set and the data set in Exercise 1. The data sets are in the same order. Describe any patterns.
61 85 67 48 54 61 59 80 67 55 88 84
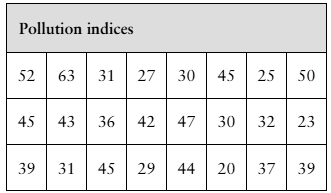
Problem 2.R.8
In Exercises 7 and 8, use the data set shown in the table at the left, which represents the pollution indices (a unitless measure of pollution ranging from 0 to 100) for 24 U.S. cities. (Adapted from Numbeo)
Use a dot plot to display the data set. Describe any patterns.
Problem 2.R.11
The heights (in feet) and the number of stories of the ten tallest buildings in New York City are listed. Use a scatter plot to display the data. Describe any patterns. (Source: Emporis)
Problem 2.Q.1g
The data set represents the number of minutes a sample of 27 people exercise each week.
108 139 120 123 120 132 123 131 131
157 150 124 111 101 135 119 116 117
127 128 139 119 118 114 127 142 130
g. Display the data using a box-and-whisker plot.
Problem 2.T.1d
The overall averages of 12 students in a statistics class prior to taking the final exam are listed.
67 72 88 73 99 85 81 87 63 94 68 87
d. Display the data in a stem-and-leaf plot. Use one line per stem.
Problem 2.T.2c
The data set represents the number of movies that a sample of 20 people watched in a year.
121 148 94 142 170 88 221 106 18 67
149 28 60 101 134 168 92 154 53 66
c. Display the data using a relative frequency histogram.
Problem 2.RE.16
For the four test scores 96, 85, 91, and 86, the first 3 test scores are 20% of the final grade, and the last test score is 40% of the final grade. Find the weighted mean of the test scores.
Problem 2.RE.2
In Exercises 1 and 2, use the data set, which represents the overall average class sizes for 20 national universities. (Adapted from Public University Honors)
37 34 42 44 39 40 41 51 49 31
52 26 31 40 30 27 36 43 48 35
Construct a relative frequency histogram using the frequency distribution in Exercise 1. Then determine which class has the greatest relative frequency and which has the least relative frequency.
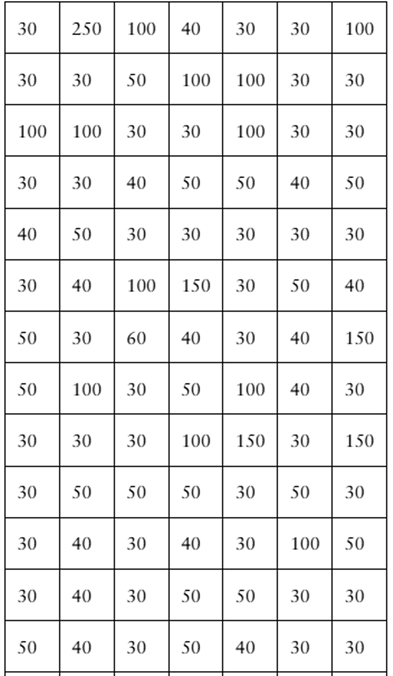
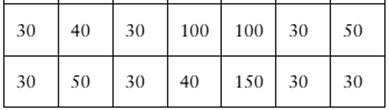
Problem 2.T.1
According to data from the city of Toronto, Ontario, Canada, there were nearly 112,000 parking infractions in the city for December 2020, with fines totaling over 5,500,000 Canadian dollars. The fines (in Canadian dollars) for a random sample of 105 parking infractions in Toronto, Ontario, Canada, for December 2020 are listed below. (Source: City of Toronto)
In Exercises 1–5, use technology. If possible, print your results.
Find the sample mean of the data.
Problem 2.CR.15a
Tail lengths (in feet) for a sample of American alligators are listed.
6.5 3.4 4.2 7.1 5.4 6.8 7.5 3.9 4.6
a. Find the mean, median, and mode of the tail lengths. Which best describes a typical American alligator tail length? Explain your reasoning.
Problem 2.T.1a
The overall averages of 12 students in a statistics class prior to taking the final exam are listed.
67 72 88 73 99 85 81 87 63 94 68 87
a. Find the mean, median, and mode of the data set. Which best represents the center of the data?
Problem 2.Q.4a
Weekly salaries (in dollars) for a sample of construction workers are listed.
1100 720 1384 1124 1255 976 718 1316
749 1062 1248 891 969 790 860 1100
a. Find the mean, median, and mode of the salaries. Which best describes a typical salary?