Car Crash Test Measurements If we use the data given in Exercise 1 with two-way analysis of variance and a 0.05 significance level, we get the accompanying display. What do you conclude?
Table of contents
- 1. Intro to Stats and Collecting Data1h 14m
- 2. Describing Data with Tables and Graphs1h 55m
- 3. Describing Data Numerically2h 5m
- 4. Probability2h 16m
- 5. Binomial Distribution & Discrete Random Variables3h 6m
- 6. Normal Distribution and Continuous Random Variables2h 11m
- 7. Sampling Distributions & Confidence Intervals: Mean3h 23m
- Sampling Distribution of the Sample Mean and Central Limit Theorem19m
- Distribution of Sample Mean - Excel23m
- Introduction to Confidence Intervals15m
- Confidence Intervals for Population Mean1h 18m
- Determining the Minimum Sample Size Required12m
- Finding Probabilities and T Critical Values - Excel28m
- Confidence Intervals for Population Means - Excel25m
- 8. Sampling Distributions & Confidence Intervals: Proportion1h 12m
- 9. Hypothesis Testing for One Sample3h 29m
- 10. Hypothesis Testing for Two Samples4h 50m
- Two Proportions1h 13m
- Two Proportions Hypothesis Test - Excel28m
- Two Means - Unknown, Unequal Variance1h 3m
- Two Means - Unknown Variances Hypothesis Test - Excel12m
- Two Means - Unknown, Equal Variance15m
- Two Means - Unknown, Equal Variances Hypothesis Test - Excel9m
- Two Means - Known Variance12m
- Two Means - Sigma Known Hypothesis Test - Excel21m
- Two Means - Matched Pairs (Dependent Samples)42m
- Matched Pairs Hypothesis Test - Excel12m
- 11. Correlation1h 6m
- 12. Regression1h 50m
- 13. Chi-Square Tests & Goodness of Fit1h 57m
- 14. ANOVA1h 57m
9. Hypothesis Testing for One Sample
Steps in Hypothesis Testing
Problem 10.1.14
Textbook Question
Testing for a Linear Correlation
In Exercises 13–28, construct a scatterplot, and find the value of the linear correlation coefficient r. Also find the P-value or the critical values of r from Table A-6. Use a significance level of α = 0.05. Determine whether there is sufficient evidence to support a claim of a linear correlation between the two variables. (Save your work because the same data sets will be used in Section 10-2 exercises.)
Powerball Jackpots and Tickets Sold Listed below are the same data from Table 10-1 in the Chapter Problem, but an additional pair of values has been added from actual Powerball results. Is there sufficient evidence to conclude that there is a linear correlation between lottery jackpots and numbers of tickets sold? Comment on the effect of the added pair of values in the last column. Compare the results to those obtained in Example 4.

 Verified step by step guidance
Verified step by step guidance1
Step 1: Construct a scatterplot. Plot the given data points on a graph where the x-axis represents the jackpot values and the y-axis represents the number of tickets sold. Each pair of values (e.g., (334, 54)) corresponds to a point on the scatterplot.
Step 2: Calculate the linear correlation coefficient (r). Use the formula for r: r = (nΣ(xy) - ΣxΣy) / sqrt([(nΣ(x^2) - (Σx)^2)][(nΣ(y^2) - (Σy)^2)]), where n is the number of data points, Σ(xy) is the sum of the products of paired values, Σx and Σy are the sums of x and y values, and Σ(x^2) and Σ(y^2) are the sums of the squares of x and y values.
Step 3: Determine the critical value of r or the P-value. Use Table A-6 to find the critical value of r for a significance level of α = 0.05 and the appropriate degrees of freedom (df = n - 2). Alternatively, calculate the P-value using statistical software or a calculator.
Step 4: Compare the calculated r value to the critical value or interpret the P-value. If |r| is greater than the critical value or if the P-value is less than α = 0.05, there is sufficient evidence to support the claim of a linear correlation.
Step 5: Analyze the effect of the added pair of values (625, 90). Recalculate the correlation coefficient and compare it to the previous results (e.g., Example 4). Discuss whether the added pair strengthens or weakens the evidence for a linear correlation.
 Verified video answer for a similar problem:
Verified video answer for a similar problem:This video solution was recommended by our tutors as helpful for the problem above
Video duration:
5mPlay a video:
Was this helpful?
Key Concepts
Here are the essential concepts you must grasp in order to answer the question correctly.
Linear Correlation Coefficient (r)
The linear correlation coefficient, denoted as r, quantifies the strength and direction of a linear relationship between two variables. Its value ranges from -1 to 1, where 1 indicates a perfect positive correlation, -1 indicates a perfect negative correlation, and 0 indicates no correlation. Understanding r is crucial for determining whether a linear relationship exists between the jackpot amounts and the number of tickets sold.
Recommended video:
Guided course
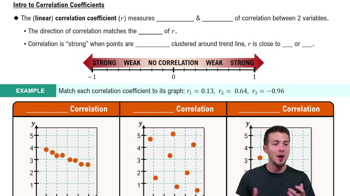
Correlation Coefficient
Scatterplot
A scatterplot is a graphical representation that displays the relationship between two quantitative variables. Each point on the plot corresponds to an observation in the dataset, with one variable plotted along the x-axis and the other along the y-axis. Creating a scatterplot helps visualize potential correlations and patterns, making it easier to interpret the data before calculating the correlation coefficient.
Recommended video:
Guided course
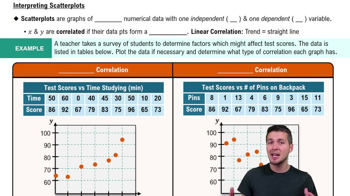
Scatterplots & Intro to Correlation
P-value and Significance Level
The P-value is a statistical measure that helps determine the significance of the results obtained from a hypothesis test. In this context, it assesses whether the observed correlation is statistically significant at a chosen significance level (α), typically set at 0.05. If the P-value is less than α, it suggests sufficient evidence to reject the null hypothesis, indicating a significant linear correlation between the two variables.
Recommended video:
Guided course
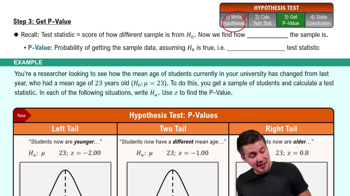
Step 3: Get P-Value

 6:21m
6:21mWatch next
Master Step 1: Write Hypotheses with a bite sized video explanation from Patrick
Start learningRelated Videos
Related Practice
Textbook Question
