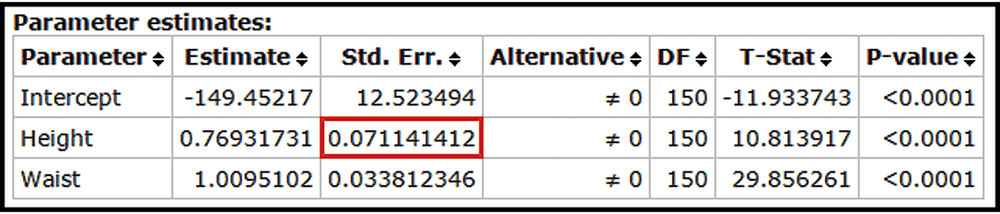
Testing Hypotheses About Regression Coefficients If the coefficient has a nonzero value, then it is helpful in predicting the value of the response variable. If it is not helpful in predicting the value of the response variable and can be eliminated from the regression equation. To test the claim that use the test statistic Critical values or P-values can be found using the t distribution with degrees of freedom, where k is the number of predictor variables and n is the number of observations in the sample. The standard error is often provided by software. For example, see the accompanying StatCrunch display for Example 1, which shows that (found in the column with the heading of “Std. Err.” and the row corresponding to the first predictor variable of height). Use the sample data in Data Set 1 “Body Data” and the StatCrunch display to test the claim that Also test the claim that What do the results imply about the regression equation?

Finding the Best Model

In Exercises 5–16, construct a scatterplot and identify the mathematical model that best fits the given data. Assume that the model is to be used only for the scope of the given data, and consider only linear, quadratic, logarithmic, exponential, and power models.

Sunspot Numbers Listed below in order by row are annual sunspot numbers beginning with 1980. Is the best model a good model? Carefully examine the scatterplot and identify the pattern of the points. Which of the models fits that pattern?

[IMAGE]

Sum of Squares Criterion In addition to the value of another measurement used to assess the quality of a model is the sum of squares of the residuals. Recall from Section 10-2 that a residual is (the difference between an observed y value and the value predicted from the model). Better models have smaller sums of squares. Refer to the U.S. population data in Table 10-7.

a. Find the sum of squares of the residuals resulting from the linear model.

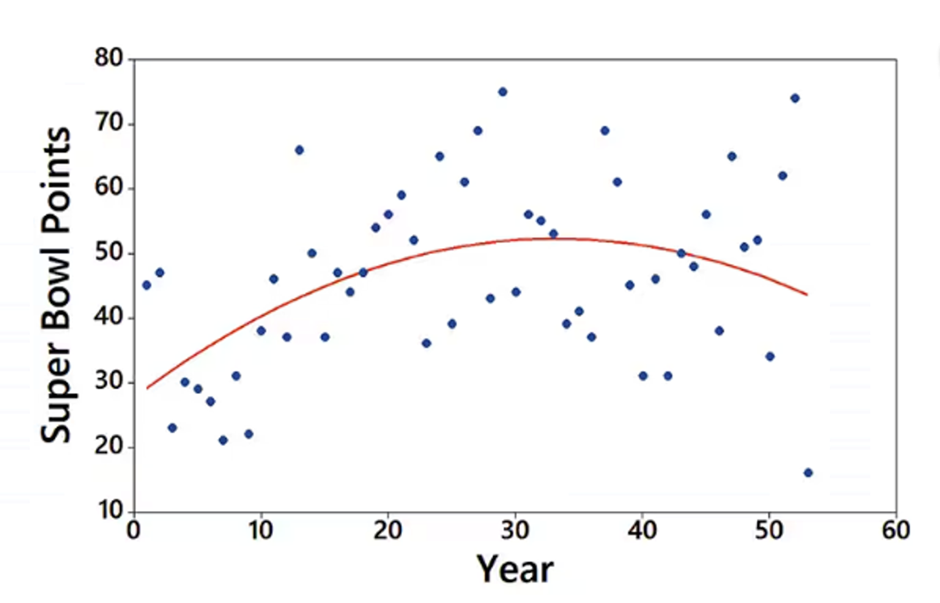
Interpreting a Graph The accompanying graph plots the numbers of points scored in each Super Bowl from the first Super Bowl in 1967 (coded as year 1) to the last Super Bowl at the time of this writing. The graph of the quadratic equation that best fits the data is also shown in red. What feature of the graph justifies the value of R^2 = 0.205 for the quadratic model?

Finding the Best Model

In Exercises 5–16, construct a scatterplot and identify the mathematical model that best fits the given data. Assume that the model is to be used only for the scope of the given data, and consider only linear, quadratic, logarithmic, exponential, and power models.

Dirt Cheap The Cherry Hill Construction company in Branford, CT sells screened topsoil by the “yard,” which is actually a cubic yard. Let the variable x be the length (yd) of each side of a cube of screened topsoil. The table below lists the values of x along with the corresponding cost (dollars).

Finding the Best Model

In Exercises 5–16, construct a scatterplot and identify the mathematical model that best fits the given data. Assume that the model is to be used only for the scope of the given data, and consider only linear, quadratic, logarithmic, exponential, and power models.

Sound Intensity The table lists intensities of sounds as multiples of a basic reference sound. A scale similar to the decibel scale is used to measure the sound intensity.

Finding the Best Model

In Exercises 5–16, construct a scatterplot and identify the mathematical model that best fits the given data. Assume that the model is to be used only for the scope of the given data, and consider only linear, quadratic, logarithmic, exponential, and power models.

Deaths from Motor Vehicle Crashes Listed below are the numbers of deaths in the United States resulting from motor vehicle crashes. Use the best model to find the projected number of such deaths for the year 2025.

Comparing Two Means Treating the data as samples from larger populations, test the claim that there is a significant difference between the mean of presidents and the mean of popes.

Testing for a Linear Correlation

In Exercises 13–28, construct a scatterplot, and find the value of the linear correlation coefficient r. Also find the P-value or the critical values of r from Table A-6. Use a significance level of α = 0.05. Determine whether there is sufficient evidence to support a claim of a linear correlation between the two variables. (Save your work because the same data sets will be used in Section 10-2 exercises.)

Powerball Jackpots and Tickets Sold Listed below are the same data from Table 10-1 in the Chapter Problem, but an additional pair of values has been added in the last column. Is there sufficient evidence to conclude that there is a linear correlation between lottery jackpot amounts and numbers of tickets sold? Comment on the effect of the added pair of values in the last column. Compare the results to those obtained in Example 4.

[IMAGE]