Least-Squares Property According to the least-squares property, the regression line minimizes the sum of the squares of the residuals. Refer to the jackpot/tickets data in Table 10-1 and use the regression equation y^ = -10.9 + 0.174x that was found in Examples 1 and 2 of this section.

a. Identify the nine residuals.

Least-Squares Property According to the least-squares property, the regression line minimizes the sum of the squares of the residuals. Refer to the jackpot/tickets data in Table 10-1 and use the regression equation y^ = -10.9 + 0.174x that was found in Examples 1 and 2 of this section.

b. Find the sum of the squares of the residuals.

Finding the Equation of the Regression Line

In Exercises 9 and 10, use the given data to find the equation of the regression line. Examine the scatterplot and identify a characteristic of the data that is ignored by the regression line.

[IMAGE]

Effects of an Outlier Refer to the Minitab-generated scatterplot given in Exercise 9 of Section 10-1

a. Using the pairs of values for all 10 points, find the equation of the regression line.

Effects of Clusters Refer to the Minitab-generated scatterplot given in Exercise 10 of Section 10-1.

a. Using the pairs of values for all 8 points, find the equation of the regression line.

Notation Using the weights (lb) and highway fuel consumption amounts (mi/gal) of the 48 cars listed in Data Set 35 “Car Data” of Appendix B, we get this regression equation:

y^ = 58.9 - 0.00749x, where x represents weight.

a. What does the symbol y^ represent?

Notation Using the weights (lb) and highway fuel consumption amounts (mi/gal) of the 48 cars listed in Data Set 35 “Car Data” of Appendix B, we get this regression equation:

y^ = 58.9 - 0.00749x, where x represents weight.

c. What is the predictor variable?

Notation What is the difference between the regression equation y^ = b0 + b1x and the regression equation y = β0 + β1x.

Best-Fit Line

What is a residual?

In what sense is the regression line the straight line that “best” fits the points in a scatterplot?

Regression and Predictions

Exercises 13–28 use the same data sets as Exercises 13–28 in Section 10-1.

Find the regression equation, letting the first variable be the predictor (x) variable.

Find the indicated predicted value by following the prediction procedure summarized in Figure 10-5.

Powerball Jackpots and Tickets Sold Listed below are the same data from Table 10-1 in the Chapter Problem, but an additional pair of values has been added from actual Powerball results. (Jackpot amounts are in millions of dollars, ticket sales are in millions.) Find the best predicted number of tickets sold when the jackpot was actually 345 million dollars. How does the result compare to the value of 55 million tickets that were actually sold?

Regression and Predictions

Exercises 13–28 use the same data sets as Exercises 13–28 in Section 10-1.

Find the regression equation, letting the first variable be the predictor (x) variable.

Find the indicated predicted value by following the prediction procedure summarized in Figure 10-5.

Taxis Use the distance/fare data from Exercise 15 and find the best predicted fare amount for a distance of 3.10 miles. How does the result compare to the actual fare of $15.30?

Making Predictions

In Exercises 5–8, let the predictor variable x be the first variable given. Use the given data to find the regression equation and the best predicted value of the response variable. Be sure to follow the prediction procedure summarized in Figure 10-5. Use a 0.05 significance level.

Bear Measurements Head widths (in.) and weights (lb) were measured for 20 randomly selected bears (from Data Set 18 “Bear Measurements” in Appendix B). The 20 pairs of measurements yield xbar = 6.9 in., ybar = 214.3 lb, r = 0.879 P-value = 0.000 and y^ = -212 + 61.9x. Find the best predicted weight of a bear given that the bear has a head width of 6.5 in.

Correlation and Slope What is the relationship between the linear correlation coefficient r and the slope b1 of a regression line?

se Notation Using Data Set 1 “Body Data” in Appendix B, if we let the predictor variable x represent heights of males and let the response variable y represent weights of males, the sample of 153 heights and weights results in se = 16.27555 cm. In your own words, describe what that value of se represents.

Coefficient of Determination Using the heights and weights described in Exercise 1, the linear correlation coefficient r is 0.394. Find the value of the coefficient of determination. What practical information does the coefficient of determination provide?

Interpreting a Computer Display

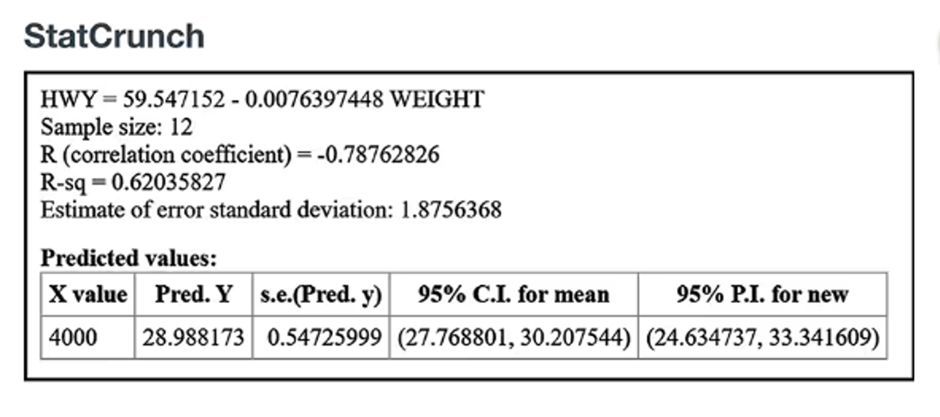
In Exercises 9–12, refer to the display obtained by using the paired data consisting of weights (pounds) and highway fuel consumption amounts (mi/gal) of the large cars included in Data Set 35 “Car Data” in Appendix B. Along with the paired weights and fuel consumption amounts, StatCrunch was also given the value of 4000 pounds to be used for predicting highway fuel consumption.

Testing for Correlation Use the information provided in the display to determine the value of the linear correlation coefficient. Is there sufficient evidence to support a claim of a linear correlation between weights of large cars and the highway fuel consumption amounts?

Interpreting the Coefficient of Determination

In Exercises 5–8, use the value of the linear correlation coefficient r to find the coefficient of determination and the percentage of the total variation that can be explained by the linear relationship between the two variables.

Times of Taxi Rides and Fares r = 0.953 (x = time in minutes, y = fare in dollars)

Interpreting the Coefficient of Determination

In Exercises 5–8, use the value of the linear correlation coefficient r to find the coefficient of determination and the percentage of the total variation that can be explained by the linear relationship between the two variables.

Times of Taxi Rides and Tips r = 0.298 (x = time in minutes, y = the amount of tip in dollars)

Standard Error of Estimate A random sample of 118 different female statistics students is obtained and their weights are measured in kilograms and in pounds. Using the 118 paired weights (weight in kg, weight in lb), what is the value of se? For a female statistics student who weighs 100 lb, the predicted weight in kilograms is 45.4 kg. What is the 95% prediction interval?

Interpreting a Computer Display

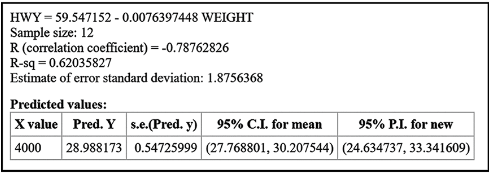
In Exercises 9–12, refer to the display obtained by using the paired data consisting of weights (pounds) and highway fuel consumption amounts (mi/gal) of the large cars included in Data Set 35 “Car Data” in Appendix B. Along with the paired weights and fuel consumption amounts, StatCrunch was also given the value of 4000 pounds to be used for predicting highway fuel consumption.

[IMAGE]

Predicting Highway Fuel Consumption Using a car weight of x = 4000 (pounds), what is the single value that is the best predicted amount of highway fuel consumption?

Interpreting a Computer Display

In Exercises 9–12, refer to the display obtained by using the paired data consisting of weights (pounds) and highway fuel consumption amounts (mi/gal) of the large cars included in Data Set 35 “Car Data” in Appendix B. Along with the paired weights and fuel consumption amounts, StatCrunch was also given the value of 4000 pounds to be used for predicting highway fuel consumption.

Finding a Prediction Interval For a car weighing 4000 pounds (x = 4000) identify the 95% prediction interval estimate of the highway fuel consumption. Write a statement interpreting that interval.

Finding a Prediction Interval

In Exercises 13–16, use the following paired data consisting of weights of large cars (pounds) and highway fuel consumption (mi/gal) from Data Set 35 “Car Data” in Appendix B. (These are the same data used in Exercises 9-12.) Let x represent the weight of the car and let y represent the corresponding highway fuel consumption. Use the given weight and the given confidence level to construct a prediction interval estimate of highway fuel consumption.

Cars Use x = 3800 pounds with a 99% confidence level.

Variation and Prediction Intervals

In Exercises 17–20, find the (a) explained variation, (b) unexplained variation, and (c) indicated prediction interval. In each case, there is sufficient evidence to support a claim of a linear correlation, so it is reasonable to use the regression equation when making predictions.

Altitude and Temperature Listed below are altitudes (thousands of feet) and outside air temperatures (°F) recorded by the author during Delta Flight 1053 from New Orleans to Atlanta. For the prediction interval, use a 95% confidence level with the altitude of 6327 ft (or 6.327 thousand feet).

Variation and Prediction Intervals

In Exercises 17–20, find the (a) explained variation, (b) unexplained variation, and (c) indicated prediction interval. In each case, there is sufficient evidence to support a claim of a linear correlation, so it is reasonable to use the regression equation when making predictions.

Weighing Seals with a Camera The table below lists overhead widths (cm) of seals measured from photographs and the weights (kg) of the seals (based on “Mass Estimation of Weddell Seals Using Techniques of Photogrammetry,” by R. Garrott of Montana State University). For the prediction interval, use a 99% confidence level with an overhead width of 9.0 cm.

Response and Predictor Variables Using all of the Tour de France bicycle race results up to a recent year, we get this multiple regression equation: Speed = 29.2-0.00260Distance + 0.540Stages + 0.0570Finishers, where Speed is the mean speed of the winner (km/h), Distance is the length of the race (km), Stages is the number of stages in the race, and Finishers is the number of bicyclists who finished the race. Identify the response and predictor variables.

Interpreting R^2 For the multiple regression equation given in Exercise 1, we get R^2 = 0.897. What does that value tell us?

Interpreting a Computer Display

In Exercises 5–8, we want to consider the correlation between heights of fathers and mothers and the heights of their sons. Refer to the StatCrunch display and answer the given questions or identify the indicated items. The display is based on Data Set 10 “Family Heights” in Appendix B. (The response y variable represents heights of sons.)

[IMAGE]

Height of Son Should the multiple regression equation be used for predicting the height of a son based on the height of his father and mother? Why or why not?

Garbage: Finding the Best Multiple Regression Equation

In Exercises 9–12, refer to the accompanying table, which was obtained by using the data from 62 households listed in Data Set 42 “Garbage Weight” in Appendix B. The response (y) variable is PLAS (weight of discarded plastic in pounds). The predictor (x) variables are METAL (weight of discarded metals in pounds), PAPER (weight of discarded paper in pounds), and GLASS (weight of discarded glass in pounds).

[IMAGE]

If only one predictor (x) variable is used to predict the weight of discarded plastic, which single variable is best? Why?

Garbage: Finding the Best Multiple Regression Equation

In Exercises 9–12, refer to the accompanying table, which was obtained by using the data from 62 households listed in Data Set 42 “Garbage Weight” in Appendix B. The response (y) variable is PLAS (weight of discarded plastic in pounds). The predictor (x) variables are METAL (weight of discarded metals in pounds), PAPER (weight of discarded paper in pounds), and GLASS (weight of discarded glass in pounds).

[IMAGE]

If exactly two predictor (x) variables are to be used to predict the weight of discarded plastic, which two variables should be chosen? Why?

Dummy Variable Refer to Data Set 18 “Bear Measurements” in Appendix B and use the sex, age, and weight of the bears. For sex, let 0 represent female and let 1 represent male. Letting the response variable represent weight, use the variable of age and the dummy variable of sex to find the multiple regression equation. Use the equation to find the predicted weight of a bear with the characteristics given below. Does sex appear to have much of an effect on the weight of a bear?

Female bear that is 20 years of age

Male bear that is 20 years of age