Textbook Question
Bootstrapping and Randomization When resampling data from two independent samples, what is the fundamental difference between bootstrapping and randomization?
9. Hypothesis Testing for One Sample
Steps in Hypothesis Testing
1:13 minutesProblem 10.2.3
Textbook Question
Best-Fit Line
What is a residual?
In what sense is the regression line the straight line that “best” fits the points in a scatterplot?
Verified step by step guidance1
A residual is the difference between the observed value of the dependent variable (y) and the predicted value (ŷ) from the regression line. Mathematically, it is expressed as: .
The regression line is considered the 'best fit' because it minimizes the sum of the squared residuals. This is known as the 'least squares criterion,' which ensures that the total squared differences between observed and predicted values are as small as possible.
To calculate the regression line, the slope () and intercept () are determined using formulas derived from the least squares method. The line is represented as: .
The slope () indicates the rate of change of the dependent variable with respect to the independent variable, while the intercept () represents the predicted value of the dependent variable when the independent variable is zero.
The regression line is optimal in the sense that it provides the best linear approximation of the relationship between the variables, reducing prediction errors and providing a clear summary of the trend in the data.
Verified video answer for a similar problem:This video solution was recommended by our tutors as helpful for the problem above
Video duration:
1mWas this helpful?
Key Concepts
Here are the essential concepts you must grasp in order to answer the question correctly.
Residuals
A residual is the difference between the observed value of a dependent variable and the value predicted by a regression model. It quantifies the error in the prediction for each data point, indicating how far off the model's predictions are from the actual data. Residuals are crucial for assessing the accuracy of a regression model and can be analyzed to identify patterns or potential issues in the model.
Best-Fit Line
The best-fit line, or regression line, is the straight line that minimizes the sum of the squared residuals in a scatterplot. This line represents the relationship between the independent and dependent variables, providing the most accurate predictions based on the available data. The method of least squares is commonly used to determine the slope and intercept of this line, ensuring it best captures the trend of the data points.
Recommended video:
Guided course
05:43
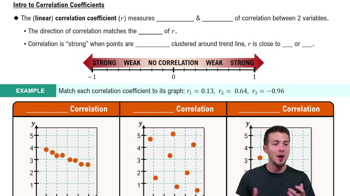
Correlation Coefficient
Scatterplot
A scatterplot is a graphical representation of two variables, where each point represents an observation in the dataset. It allows for visual assessment of the relationship between the variables, helping to identify trends, correlations, or outliers. The arrangement of points in a scatterplot can indicate whether a linear model is appropriate for the data, guiding the selection of the best-fit line.
Recommended video:
Guided course
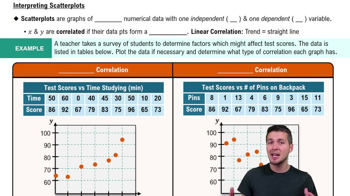
06:36Scatterplots & Intro to Correlation
6:21mWatch next
Master Step 1: Write Hypotheses with a bite sized video explanation from Patrick
Start learningRelated Videos
Related Practice