Back
BackProblem 7.1.56
Writing A null hypothesis is rejected with a level of significance of 0.10. Is it also rejected at a level of significance of 0.05? Explain.
Problem 7.1.58
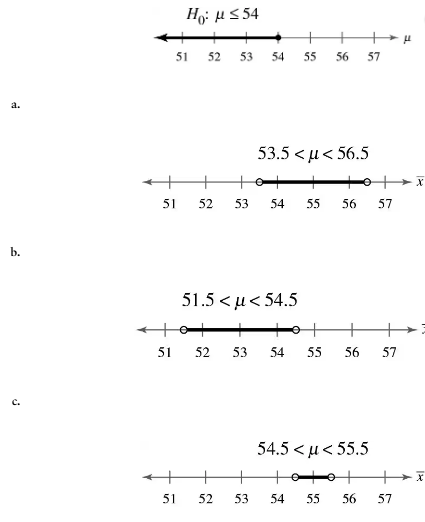
Graphical Analysis In Exercises 57–60, you are given a null hypothesis and three confidence intervals that represent three samplings. Determine whether each confidence interval indicates that you should reject H0. Explain your reasoning.
Problem 7.1.59
Graphical Analysis In Exercises 57–60, you are given a null hypothesis and three confidence intervals that represent three samplings. Determine whether each confidence interval indicates that you should reject H0. Explain your reasoning.
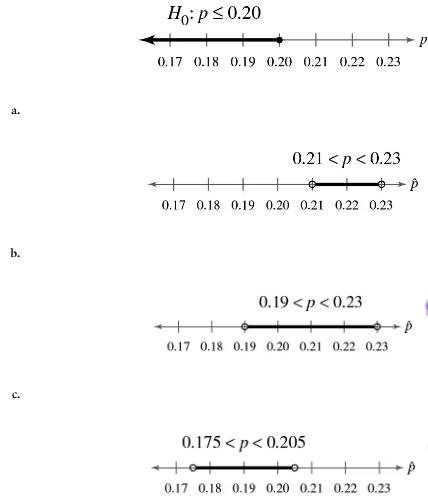
Problem 7.1.60
Graphical Analysis In Exercises 57–60, you are given a null hypothesis and three confidence intervals that represent three samplings. Determine whether each confidence interval indicates that you should reject H0. Explain your reasoning.
Problem 7.1.11
Stating Hypotheses In Exercises 11–16, the statement represents a claim. Write its complement and state which is H0 and which is Ha.
μ ≤ 645
Problem 7.1.22
Identifying a Test In Exercises 21–24, determine whether the hypothesis test is left-tailed, right-tailed, or two-tailed.
Ha: μ ≥ 5.2
H0: μ < 5.2
Problem 7.1.23
Identifying a Test In Exercises 21–24, determine whether the hypothesis test is left-tailed, right-tailed, or two-tailed.
Ha: σ^2 = 142
H0: σ ≠ 142
Problem 7.1.27
Stating the Null and Alternative Hypotheses In Exercises 25–30, write the claim as a mathematical statement. State the null and alternative hypotheses, and identify which represents the claim.
Base Price of an ATV The standard deviation of the base price of an all-terrain vehicle is no more than $320.
Problem 7.1.24
Identifying a Test In Exercises 21–24, determine whether the hypothesis test is left-tailed, right-tailed, or two-tailed.
Ha: p = 0.25
H0: p ≠ 0.25
Problem 7.1.31
Identifying Type I and Type II Errors In Exercises 31–36, describe type I and type II errors for a hypothesis test of the indicated claim.
Repeat Customers A used textbook selling website claims that at least 60% of its new customers will return to buy their next textbook.
Problem 7.1.33
Identifying Type I and Type II Errors In Exercises 31–36, describe type I and type II errors for a hypothesis test of the indicated claim.
Chess A local chess club claims that the length of time to play a game has a standard deviation of more than 12 minutes.
Problem 7.1.34
Identifying Type I and Type II Errors In Exercises 31–36, describe type I and type II errors for a hypothesis test of the indicated claim.
Video Game Systems A researcher claims that the percentage of U.S. gamers that are women is not 50%.
Problem 7.1.12
Stating Hypotheses In Exercises 11–16, the statement represents a claim. Write its complement and state which is H0 and which is Ha.
μ < 128
Problem 7.1.13
Stating Hypotheses In Exercises 11–16, the statement represents a claim. Write its complement and state which is H0 and which is Ha.
σ ≠ 5
Problem 7.2.26
Finding Critical Values and Rejection Regions In Exercises 23–28, find the critical value(s) and rejection region(s) for the type of z-test with level of significance α. Include a graph with your answer.
Right-tailed test, α = 0.08
Problem 7.2.46
Writing In a right-tailed test where P < alpha, does the standardized test statistic lie to the left or the right of the critical value? Explain your reasoning.
Problem 7.2.10
Graphical Analysis In Exercises 9–12, match the P-value or z-statistic with the graph that represents the corresponding area. Explain your reasoning.
P= 0.2802
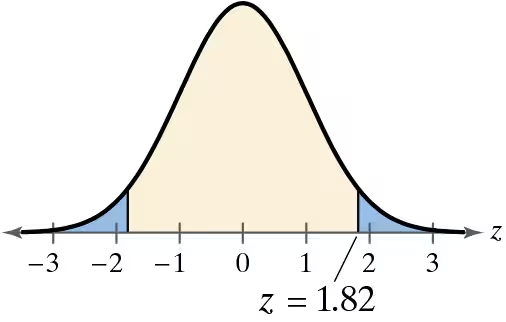
Problem 7.2.11
Graphical Analysis In Exercises 9–12, match the P-value or z-statistic with the graph that represents the corresponding area. Explain your reasoning.
z = -2.37
Problem 7.2.12
Graphical Analysis In Exercises 9–12, match the P-value or z-statistic with the graph that represents the corresponding area. Explain your reasoning.
z = -0.51
Problem 7.2.17
Finding a P-Value In Exercises 13–18, find the P-value for the hypothesis test with the standardized test statistic z. Decide whether to reject H0 for the level of significance alpha.
Left-tailed test
z=-1.68
alpha=0.05
Problem 7.2.18
Finding a P-Value In Exercises 13–18, find the P-value for the hypothesis test with the standardized test statistic z. Decide whether to reject H0 for the level of significance alpha.
Left-tailed test
z= 1.95
alpha=0.08
Problem 7.2.24
Finding Critical Values and Rejection Regions In Exercises 23–28, find the critical value(s) and rejection region(s) for the type of z-test with level of significance α. Include a graph with your answer.
Left-tailed test, α = 0.09
Problem 7.2.28
Finding Critical Values and Rejection Regions In Exercises 23–28, find the critical value(s) and rejection region(s) for the type of z-test with level of significance α. Include a graph with your answer.
Two-tailed test, α = 0.12
Problem 7.2.31
In Exercises 29–32, test the claim about the population mean at the level of significance α. Assume the population is normally distributed.
Claim: ; μ ≠ 5880; α = 0.03; α = 413
Sample statistics: x_bar = 5771, n = 67
Problem 7.2.32
In Exercises 29–32, test the claim about the population mean at the level of significance α. Assume the population is normally distributed.
Claim: ; μ ≤ 22,500; α = 0.01; α = 1200
Sample statistics: x_bar = 23,500, n = 45
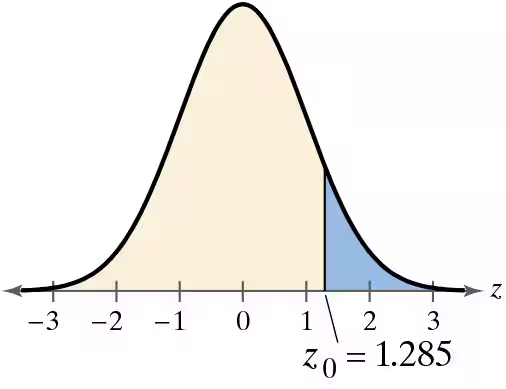
Problem 7.2.21
Graphical Analysis In Exercises 21 and 22, state whether each standardized test statistic z allows you to reject the null hypothesis. Explain your reasoning.
a. z = -1.301
b. z = 1.203
c. z = 1.280
d. z = 1.286
Problem 7.2.33
Hypothesis Testing Using a P-Value In Exercises 33–38,
a. identify the claim and state and .
b. find the standardized test statistic z.
c. find the corresponding P-value.
d. decide whether to reject or fail to reject the null hypothesis.
e. interpret the decision in the context of the original claim.
MCAT Scores A random sample of 100 medical school applicants at a university has a mean total score of 505 on the MCAT. According to a report, the mean total score for the school’s applicants is more than 503. Assume the population standard deviation is 10.6. At alpha=0.01, is there enough evidence to support the report’s claim?
Problem 7.2.34
Hypothesis Testing Using a P-Value In Exercises 33–38,
a. identify the claim and state and .
b. find the standardized test statistic z.
c. find the corresponding P-value.
d. decide whether to reject or fail to reject the null hypothesis.
e. interpret the decision in the context of the original claim.
Sprinkler Systems A manufacturer of sprinkler systems designed for fire protection claims that the average activating temperature is at least 135°F. To test this claim, you randomly select a sample of 32 systems and find the mean activation temperature to be 133°F. Assume the population standard deviation is 3.3°F. At alpha=0.10, do you have enough evidence to reject the manufacturer’s claim?
Problem 7.2.42
Hypothesis Testing Using Rejection Region(s) In Exercises 39–44, (a) identify the claim and state H0 and Ha, (b) find the critical value(s) and identify the rejection region(s), (c) find the standardized test statistic z, (d) decide whether to reject or fail to reject the null hypothesis, and (e) interpret the decision in the context of the original claim.
Light Bulbs A light bulb manufacturer guarantees that the mean life of a certain type of light bulb is at least 750 hours. A random sample of 25 light bulbs has a mean life of 745 hours. Assume the population is normally distributed and the population standard deviation is 60 hours. At alpha= 0.02, do you have enough evidence to reject the manufacturer’s claim?
Problem 7.2.43
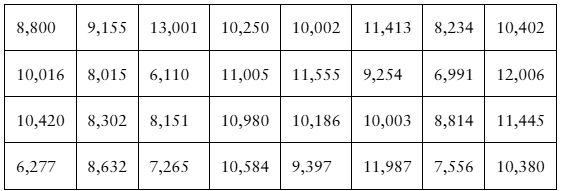
Hypothesis Testing Using Rejection Region(s) In Exercises 39–44, (a) identify the claim and state H0 and Ha, (b) find the critical value(s) and identify the rejection region(s), (c) find the standardized test statistic z, (d) decide whether to reject or fail to reject the null hypothesis, and (e) interpret the decision in the context of the original claim.
[APPLET] Fluorescent Lamps A compact fluorescent lamp (CFL) bulb manufacturer guarantees that the mean life of a CFL bulb is at least 10,000 hours. You want to test this guarantee. To do so, you record the lives of a random sample of 32 CFL bulbs. The results (in hours) are listed. Assume the population standard deviation is 1850 hours. At alpha=0.11, do you have enough evidence to reject the manufacturer’s claim?