Back
BackProblem 6.T.3b
The data set represents the scores of 12 randomly selected students on the SAT Physics Subject Test. Assume the population test scores are normally distributed and the population standard deviation is 108. (Adapted from The College Board)
b. Construct a 90% confidence interval for the population mean. Interpret the results.
Problem 6.T.4a
Use the standard normal distribution or the t-distribution to construct the indicated confidence interval for the population mean of each data set. Justify your decision. If neither distribution can be used, explain why. Interpret the results.
a. In a random sample of 40 patients, the mean waiting time at a dentist’s office was 20 minutes and the standard deviation was 7.5 minutes. Construct a 95% confidence interval for the population mean.
Problem 6.R.1
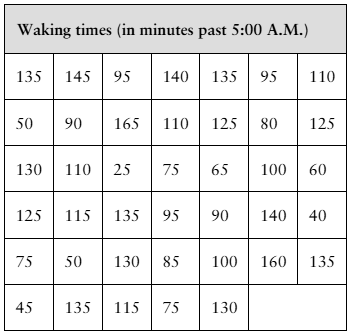
[APPLET] The waking times (in minutes past 5:00 A.M.) of 40 people who start work at 8:00 A.M. are shown in the table at the left. Assume the population standard deviation is 45 minutes. Find (a) the point estimate of the population mean μ and (b) the margin of error for a 90% confidence interval.
Problem 6.R.3
(a) Construct a 90% confidence interval for the population mean in Exercise 1. Interpret the results. (b) Does it seem likely that the population mean could be within 10% of the sample mean? Explain.
Problem 6.R.5
In Exercises 5 and 6, use the confidence interval to find the margin of error and the sample mean.
(20.75, 24.10)
Problem 6.R.6
In Exercises 5 and 6, use the confidence interval to find the margin of error and the sample mean.
(7.428, 7.562)
Problem 6.R.7
Determine the minimum sample size required to be 95% confident that the sample mean waking time is within 10 minutes of the population mean waking time. Use the population standard deviation from Exercise 1.
Problem 6.R.11
In Exercises 9–12, find the critical value tc for the level of confidence c and sample size n.
c = 0.98, n = 15
Problem 6.R.13
In Exercises 13–16, (a) find the margin of error for the values of c, s, and n, and (b) construct the confidence interval for using the t-distribution. Assume the population is normally distributed.
c = 0.90, s = 25.6, n = 16, xbar = 72.1
Problem 6.R.15
In Exercises 13–16, (a) find the margin of error for the values of c, s, and n, and (b) construct the confidence interval for using the t-distribution. Assume the population is normally distributed.
c = 0.98, s = 0.9, n = 12, xbar = 6.8
Problem 6.R.16
In Exercises 13–16, (a) find the margin of error for the values of c, s, and n, and (b) construct the confidence interval for using the t-distribution. Assume the population is normally distributed.
c = 0.99, s = 16.5, n = 20, xbar = 25.2
Problem 6.Q.1a
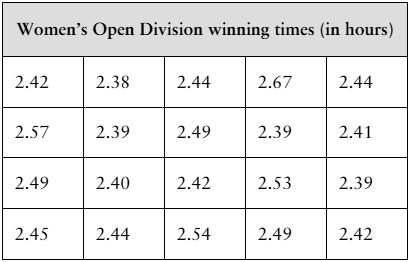
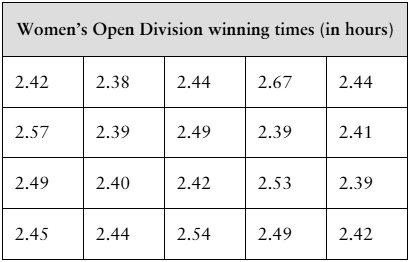
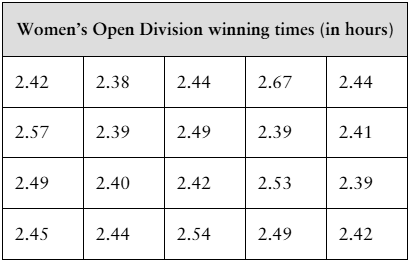
[APPLET] The winning times (in hours) for a sample of 20 randomly selected Boston Marathon Women’s Open Division champions from 1980 to 2019 are shown in the table at the left. Assume the population standard deviation is 0.068 hour. (Source: Boston Athletic Association)
a. Find the point estimate of the population mean.
Problem 6.Q.1b
[APPLET] The winning times (in hours) for a sample of 20 randomly selected Boston Marathon Women’s Open Division champions from 1980 to 2019 are shown in the table at the left. Assume the population standard deviation is 0.068 hour. (Source: Boston Athletic Association)
b. Find the margin of error for a 95% confidence level.
Problem 6.Q.1d
[APPLET] The winning times (in hours) for a sample of 20 randomly selected Boston Marathon Women’s Open Division champions from 1980 to 2019 are shown in the table at the left. Assume the population standard deviation is 0.068 hour. (Source: Boston Athletic Association)
d. Does it seem likely that the population mean could be greater than 2.52 hours? Explain.
Problem 6.Q.2
You wish to estimate the mean winning time for Boston Marathon Women’s Open Division champions. The estimate must be within 2 minutes of the population mean. Determine the minimum sample size required to construct a 99% confidence interval for the population mean. Use the population standard deviation from Exercise 1.
Problem 6.Q.3c
The data set represents the amounts of time (in minutes) spent checking email for a random sample of employees at a company.
c. Repeat part (b), assuming σ = 3.5 minutes. Compare the results.
Problem 6.Q.4
In a random sample of 12 senior-level civil engineers, the mean annual earnings were $133,326 and the standard deviation was $36,729. Assume the annual earnings are normally distributed and construct a 95% confidence interval for the population mean annual earnings for senior-level civil engineers. Interpret the results. (Adapted from Salary.com)
Problem 6.Q.5
You research the salaries of senior-level civil engineers and find that the population mean is $131,935. In Exercise 4, does the t-value fall between -t0.95 and t0.95?
Problem 6.T.2b
The data set represents the weights (in pounds) of 10 randomly selected black bears from northeast Pennsylvania. Assume the weights are normally distributed. (Source: Pennsylvania Game Commission)
b. Construct a 95% confidence interval for the population mean. Interpret the results.
Problem 6.R.8
Determine the minimum sample size required to be 99% confident that the sample mean driving distance to work is within 2 miles of the population mean driving distance to work. Use the population standard deviation from Exercise 2.
Problem 6.T.3c
The data set represents the scores of 12 randomly selected students on the SAT Physics Subject Test. Assume the population test scores are normally distributed and the population standard deviation is 108. (Adapted from The College Board)
c. Would it be unusual for the population mean to be under 575? Explain.
Problem 6.T.3d
The data set represents the scores of 12 randomly selected students on the SAT Physics Subject Test. Assume the population test scores are normally distributed and the population standard deviation is 108. (Adapted from The College Board)
d. Determine the minimum sample size required to be 95% confident that the sample mean test score is within 10 points of the population mean test score.
Problem 6.T.4b
Use the standard normal distribution or the t-distribution to construct the indicated confidence interval for the population mean of each data set. Justify your decision. If neither distribution can be used, explain why. Interpret the results.
b. In a random sample of 15 cereal boxes, the mean weight was 11.89 ounces. Assume the weights of the cereal boxes are normally distributed and the population standard deviation is 0.05 ounce. Construct a 90% confidence interval for the population mean.
Problem 6.R.17
In a random sample of 36 top-rated roller coasters, the average height is 165 feet and the standard deviation is 67 feet. Construct a 90% confidence interval for μ. Interpret the results. (Source: POP World Media, LLC)
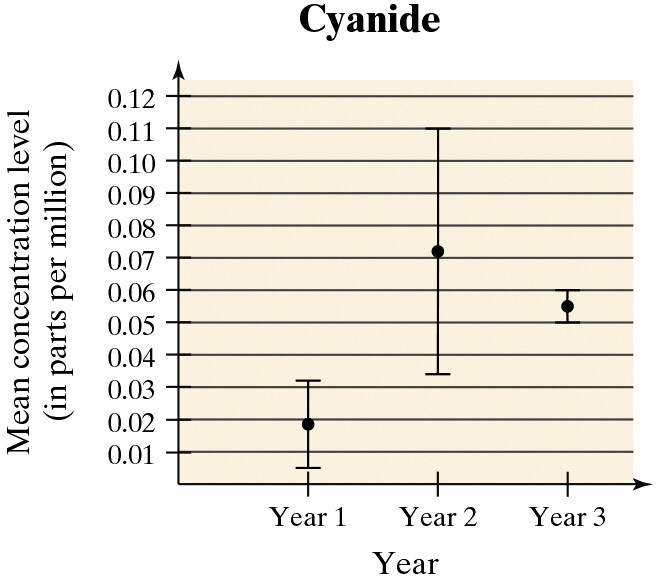
Problem 6.RSRD.3
The Safe Drinking Water Act, which was passed in 1974, allows the Environmental Protection Agency (EPA) to regulate the levels of contaminants in drinking water. The EPA requires that water utilities give their customers water quality reports annually. These reports include the results of daily water quality monitoring, which is performed to determine whether drinking water is safe for consumption. A water department tests for contaminants at water treatment plants and at customers’ taps. These contaminants include microorganisms, organic chemicals, and inorganic chemicals, such as cyanide. Cyanide’s presence in drinking water is the result of discharges from steel, plastics, and fertilizer factories. For drinking water, the maximum contaminant level of cyanide is 0.2 parts per million. As part of your job for your city’s water department, you are preparing a report that includes an analysis of the results shown in the figure at the right. The figure shows the point estimates for the population mean concentration and the 95% confidence intervals for cyanide over a three-year period. The data are based on random water samples taken by the city’s three water treatment plants.
The confidence interval for Year 2 is much larger than that for the other years. What do you think may have caused this larger confidence level?
Problem 6.RSRD.4
The Safe Drinking Water Act, which was passed in 1974, allows the Environmental Protection Agency (EPA) to regulate the levels of contaminants in drinking water. The EPA requires that water utilities give their customers water quality reports annually. These reports include the results of daily water quality monitoring, which is performed to determine whether drinking water is safe for consumption. A water department tests for contaminants at water treatment plants and at customers’ taps. These contaminants include microorganisms, organic chemicals, and inorganic chemicals, such as cyanide. Cyanide’s presence in drinking water is the result of discharges from steel, plastics, and fertilizer factories. For drinking water, the maximum contaminant level of cyanide is 0.2 parts per million. As part of your job for your city’s water department, you are preparing a report that includes an analysis of the results shown in the figure at the right. The figure shows the point estimates for the population mean concentration and the 95% confidence intervals for cyanide over a three-year period. The data are based on random water samples taken by the city’s three water treatment plants.
What can the water department do to decrease the size of the confidence intervals, regardless of the amount of variance in cyanide levels?
Problem 6.R.19
In Exercises 19–22, let p be the population proportion for the situation. (a) Find point estimates of p and q, (b) construct 90% and 95% confidence intervals for p, and (c) interpret the results of part (b) and compare the widths of the confidence intervals.
In a survey of 912 U.S. adults in Generation Z (born after 1996), 383 said they are at least somewhat likely to consider an electric vehicle for their next vehicle purchase. (Adapted from Pew Research Center)
Problem 6.R.21
In Exercises 19–22, let p be the population proportion for the situation. (a) Find point estimates of p and q, (b) construct 90% and 95% confidence intervals for p, and (c) interpret the results of part (b) and compare the widths of the confidence intervals.
In a survey of 73,901 college graduates, 23,991 obtained a postgraduate degree. (Adapted from Gallup)
Problem 6.R.25a
You wish to estimate, with 95% confidence, the population proportion of U.S. adults who have taken or planned to take a winter vacation in a recent year. Your estimate must be accurate within 5% of the population proportion.
a. No preliminary estimate is available. Find the minimum sample size needed.
Problem 6.T.1a
In a survey of 2096 U.S. adults, 1740 think football teams of all levels should require players who suffer a head injury to take a set amount of time off from playing to recover. (Adapted from The Harris Poll)
a. Find the point estimate for the population proportion.