In Exercises 1– 4, classify the two samples as independent or dependent and justify your answer.

Sample 1: The retail prices of 20 motorcycles

Sample 2: The retail prices of 20 minivans

In Exercises 3 – 6, construct the indicated confidence interval for the population mean . Which distribution did you use to create the confidence interval?

c=0.95, x̅=3.46, s=1.63, n=16

In Exercises 3 – 6, construct the indicated confidence interval for the population mean . Which distribution did you use to create the confidence interval?

c=0.90, x̅=8.21, σ=0.62, n=8

[APPLET] The annual earnings (in dollars) for 30 randomly selected locksmiths are shown below. Assume the population is normally distributed. (Adapted from Salary.com)

48,694 46,856 42,912 61,672 71,112 54,861 

69,454 71,841 59,751 69,612 54,284 52,166

66,360 48,164 65,272 35,250 61,127 65,397

58,925 58,916 59,017 53,070 45,199 69,941

69,492 57,085 53,829 52,692 68,298 53,792

Construct a 95% confidence interval for the population mean annual earnings for locksmiths.

In Exercises 1– 4, classify the two samples as independent or dependent and justify your answer.

Sample 1: The heights of 37 children

Sample 2: The heights of the same 37 children after 1 year

In Exercises 19 –22, test the claim about the mean of the differences for a population of paired data at the level of significance α. Assume the samples are random and dependent, and the populations are normally distributed.

Claim: μd<0; α=0.10.

Sample statistics: d̄=3.2, sd=5.68, n=25

In Exercises 19 –22, test the claim about the mean of the differences for a population of paired data at the level of significance α. Assume the samples are random and dependent, and the populations are normally distributed.

Claim: μd≠0; α=0.05.

Sample statistics: d̄=17.5, sd=4.05, n=37

The mean room rate for two adults for a random sample of 26 three-star hotels in Cincinnati has a sample standard deviation of $31. Assume the population is normally distributed. (Adapted from Expedia)

Construct a 99% confidence interval for the population variance.

[APPLET] The annual earnings (in dollars) for 30 randomly selected locksmiths are shown below. Assume the population is normally distributed. (Adapted from Salary.com)

48,694 46,856 42,912 61,672 71,112 54,861 

69,454 71,841 59,751 69,612 54,284 52,166

66,360 48,164 65,272 35,250 61,127 65,397

58,925 58,916 59,017 53,070 45,199 69,941

69,492 57,085 53,829 52,692 68,298 53,792

A researcher claims that the mean annual earnings for locksmiths is $55,000. At α=0.05, can you reject the researcher’s claim? Interpret the decision in the context of the original claim.

In Exercises 5– 8, test the claim about the difference between two population means μ1 and μ2 at the level of significance α. Assume the samples are random and independent, and the populations are normally distributed.

Claim: μ1>μ2; α=0.05

Population statistics: σ1= 0.30 and σ2= 0.23

Sample statistics: x̅1 = 1.28, n1 = 96, and x̅2= 1.34, n2= 85

In Exercises 9 and 10, (a) identify the claim and state Ho and Ha , (b) find the critical value(s) and identify the rejection region(s), (c) find the standardized test statistic z, (d) decide whether to reject or fail to reject the null hypothesis, and (e) interpret the decision in the context of the original claim. Assume the samples are random and independent, and the populations are normally distributed.

A researcher claims that the mean sodium content of sandwiches at Restaurant A is less than the mean sodium content of sandwiches at Restaurant B. The mean sodium content of 22 randomly selected sandwiches at Restaurant A is 670 milligrams. Assume the population standard deviation is 20 milligrams. The mean sodium content of 28 randomly selected sandwiches at Restaurant B is 690 milligrams. Assume the population standard deviation is 30 milligrams. At α=0.05, is there enough evidence to support the claim?

In a survey of 4860 U.S. adults, 77% said they would date or have already dated someone whose religion was different from theirs. (Source: Pew Research Center)

Construct a 95% confidence interval for the proportion of U.S. adults who say they would date or have already dated someone whose religion was different from theirs.

In Exercises 23 and 24, (a) identify the claim and state Ho and Ha , (b) find the critical value(s) and identify the rejection region(s), (c) calculate d̄ and sd, (d) find the standardized test statistic t, (e) decide whether to reject or fail to reject the null hypothesis, and (f) interpret the decision in the context of the original claim. Assume the samples are random and dependent, and the populations are normally distributed.

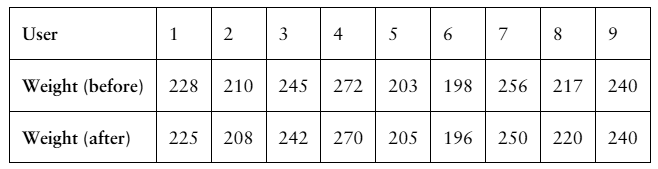
A physical fitness instructor claims that a weight loss supplement will help users lose weight after two weeks. The table shows the weights (in pounds) of 9 adults before using the supplement and two weeks after using the supplement. At α=0.10, is there enough evidence to support the physical fitness instructor’s claim?

Confounding Variables A pharmaceutical company has applied for approval to market a new arthritis medication. The research involved a test group that was given the medication and another test group that was given a placebo. Describe some possible confounding variables that could influence the results of the study.

In Exercises 25 –28, determine whether a normal sampling distribution can be used. If it can be used, test the claim about the difference between two population proportions p1 and p2 at the level of significance α. Assume the samples are random and independent.

Claim: p1<p2; α=0.05

Sample statistics: x1 = 86, n1=900 and x2 = 107, n2 = 1200

In Exercises 11–16, test the claim about the difference between two population means μ1 and μ2 at the level of significance α. Assume the samples are random and independent, and the populations are normally distributed.

Claim: μ1> μ2; α=0.10. Assume (σ1)^2 ≠ (σ2)^2

Sample statistics: x̅1= 520, s1= 25, n1= 7 and x̅2= 500, s2= 55, n2= 6

In Exercises 11–16, test the claim about the difference between two population means μ1 and μ2 at the level of significance α. Assume the samples are random and independent, and the populations are normally distributed.

Claim: μ1< μ2; α=0.10. Assume (σ1)^2 ≠ (σ2)^2

Sample statistics: x̅1=0.015, s1=0.011, n1= 8 and x̅2=0.019, s2=0.004, n2= 6

In Exercises 1– 4, classify the two samples as independent or dependent and justify your answer.

Sample 1: The fuel efficiencies of 12 cars

Sample 2: The fuel efficiencies of the same 12 cars using an alternative fuel

In Exercises 1– 4, classify the two samples as independent or dependent and justify your answer.

Sample 1: The weights of 45 oranges

Sample 2: The weights of 40 grapefruits

In Exercises 7–10, the statement represents a claim. Write its complement and state which is Ho and which is Ha.

σ=0.63

Take this quiz as you would take a quiz in class. After you are done, check your work against the answers given in the back of the book.For each exercise, perform the steps below.

a. Identify the claim and state Ho and Ha

b. Determine whether the hypothesis test is left-tailed, right-tailed, or two-tailed, and whether to use a z-test or a t-test. Explain your reasoning.

c. Find the critical value(s) and identify the rejection region(s).

d. Find the appropriate standardized test statistic.

e. Decide whether to reject or fail to reject the null hypothesis.

f. Interpret the decision in the context of the original claim.

A music teacher claims that the mean scores on a music assessment test for eighth grade students in public and private schools are equal. The mean score for 13 randomly selected public school students is 146 with a standard deviation of 49, and the mean score for 15 randomly selected private school students is 160 with a standard deviation of 42. At α=0.1, can you reject the teacher’s claim? Assume the populations are normally distributed and the population variances are equal. (Adapted from National Center for Education Statistics)

Take this test as you would take a test in class.For each exercise, perform the steps below.

a. Identify the claim and state and

b.Determine whether the hypothesis test is left-tailed, right-tailed, or two-tailed, and whether to use a z-test or a t-test. Explain your reasoning.

c.Find the critical value(s) and identify the rejection region(s).

d. Find the appropriate standardized test statistic.

e. Decide whether to reject or fail to reject the null hypothesis.

f. Interpret the decision in the context of the original claim.

A demographics researcher claims that the mean household income in a recent year is different for native-born households and foreign-born households. A sample of 18 native-born households has a mean household income of $69,474 and a standard deviation of $21,249. A sample of 21 foreign-born households has a mean household income of $64,900 and a standard deviation of $17,896. At α=0.01, can you support the demographics researcher’s claim? Assume the populations are normally distributed and the population variances are not equal. (Adapted from U.S. Census Bureau)

In Exercises 29 and 30, (a) identify the claim and state Ho and Ha, (b) find the critical value(s) and identify the rejection region(s), (c) find the standardized test statistic z, (d) decide whether to reject or fail to reject the null hypothesis, and (e) interpret the decision in the context of the original claim. Assume the samples are random and independent.

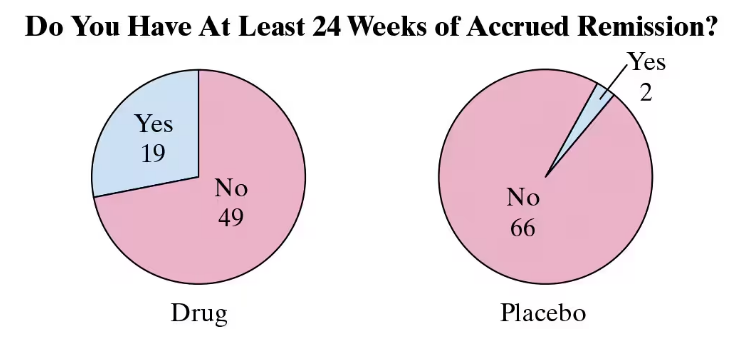
A medical research team conducted a study to test the effect of a drug used to treat a type of inflammation. In the study, 68 subjects took the drug and 68 subjects took a placebo. The results are shown below. At α=0.05, can you reject the claim that the proportion of subjects who had at least 24 weeks of accrued remission is the same for the two groups? (Source: The New England Journal of Medicine)

Take this quiz as you would take a quiz in class. After you are done, check your work against the answers given in the back of the book.For each exercise, perform the steps below.

a. Identify the claim and state Ho and Ha

b. Determine whether the hypothesis test is left-tailed, right-tailed, or two-tailed, and whether to use a z-test or a t-test. Explain your reasoning.

c. Find the critical value(s) and identify the rejection region(s).

d. Find the appropriate standardized test statistic.

e. Decide whether to reject or fail to reject the null hypothesis.

f. Interpret the decision in the context of the original claim.

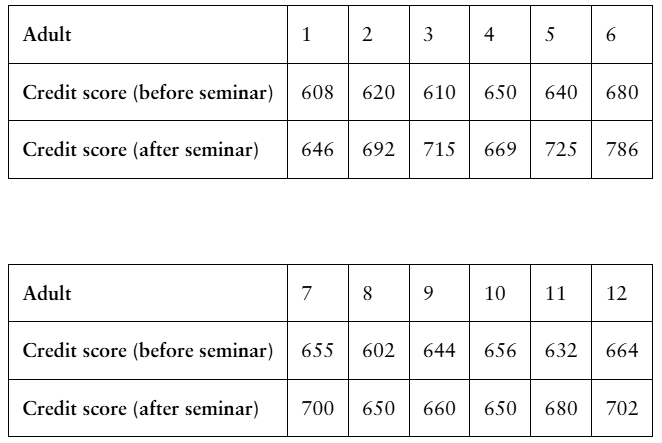
[APPLET] The table shows the credit scores for 12 randomly selected adults who are considered high-risk borrowers before and two years after they attend a personal finance seminar. At α=0.01, is there enough evidence to support the claim that the personal finance seminar helps adults increase their credit scores? Assume the populations are normally distributed.

Independent and Dependent Samples In Exercises 5– 8, classify the two samples as independent or dependent and justify your answer.

Sample 1: The maximum bench press weights for 53 football players

Sample 2: The maximum bench press weights for the same 53 football players after completing a weight lifting program

Explain how to perform a two-sample z-test for the difference between two population means using independent samples with and known.

Describe another way you can perform a hypothesis test for the difference between the means of two populations using independent samples with and known that does not use rejection regions.

Independent and Dependent Samples In Exercises 5– 8, classify the two samples as independent or dependent and justify your answer.

Sample 1: The commute times of 10 workers when they use their own vehicles

Sample 2: The commute times of the same 10 workers when they use public transportation

In Exercises 11 –14, test the claim about the difference between two population means and at the level of significance . Assume the samples are random and independent, and the populations are normally distributed.

Claim: μ1<μ2; α=0.05

Population statistics:σ1=75 and σ2=105

Sample Statistics: x̅1=2435, n1=35, x̅2=2432, n2=90

In Exercises 11 –14, test the claim about the difference between two population means and at the level of significance . Assume the samples are random and independent, and the populations are normally distributed.

Claim: μ1<μ2; α=0.03

Population statistics:σ1=136 and σ2=215

Sample Statistics: x̅1=5004, n1=144, x̅2=4895, n2=156