Back
BackProblem 7.5.29
Hypothesis Testing Using Rejection Regions In Exercises 23–30, (a) identify the claim and state H0 and Ha, (b) find the critical value(s) and identify the rejection region(s), (c) find the standardized test statistic X^2, (d) decide whether to reject or fail to reject the null hypothesis, and (e) interpret the decision in the context of the original claim. Assume the population is normally distributed.
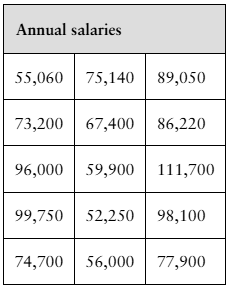
Salaries The annual salaries (in dollars) of 15 randomly chosen senior level graphic design specialists are shown in the table at the left. At α=0.05, is there enough evidence to support the claim that the standard deviation of the annual salaries is different from $13,056?
Problem 7.5.30
Hypothesis Testing Using Rejection Regions In Exercises 23–30, (a) identify the claim and state H0 and Ha, (b) find the critical value(s) and identify the rejection region(s), (c) find the standardized test statistic X^2, (d) decide whether to reject or fail to reject the null hypothesis, and (e) interpret the decision in the context of the original claim. Assume the population is normally distributed.
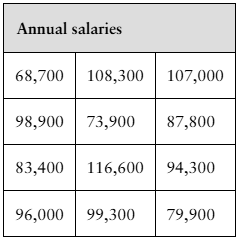
Salaries The annual salaries (in dollars) of 12 randomly chosen nursing supervisors are shown in the table at the left. At α=0.10, is there enough evidence to reject the claim that the standard deviation of the annual salaries is $18,630?
Problem 7.5.19
In Exercises 15–22, test the claim about the population variance or standard deviation at the level of significance Assume the population is normally distributed.
Claim: σ<40, α=0.01 . Sample statistics: s=40.8, n=12
Problem 7.5.20
In Exercises 15–22, test the claim about the population variance or standard deviation at the level of significance Assume the population is normally distributed.
Claim: σ^2>19, α=0.1. Sample statistics: s^2=28, n=17
Problem 7.5.16
In Exercises 15–22, test the claim about the population variance or standard deviation at the level of significance Assume the population is normally distributed.
Claim: σ^2=63, α=0.01 . Sample statistics: s^2=58, n=29
Problem 7.5.2
Can a critical value for the chi-square test be negative? Explain.
Problem 7.5.3
How do the critical values for a two-tailed test change as alpha decreases?
Problem 7.5.5
How do the requirements for a chi-square test for a variance or standard deviation differ from a z-test or a t-test for a mean?
Problem 7.5.6
Explain how to test a population variance or a population standard deviation.
Problem 7.5.8
In Exercises 7–12, find the critical value(s) and rejection region(s) for the type of chi-square test with sample size n and level of significance α.
Right-tailed test, n=10,α=0.10
Problem 7.5.9
In Exercises 7–12, find the critical value(s) and rejection region(s) for the type of chi-square test with sample size n and level of significance α.
Left-tailed test, n=7,α=0.01
Problem 7.5.12
In Exercises 7–12, find the critical value(s) and rejection region(s) for the type of chi-square test with sample size n and level of significance α.
Two-tailed test, n=61,α=0.01
Problem 7.5.7
In Exercises 7–12, find the critical value(s) and rejection region(s) for the type of chi-square test with sample size n and level of significance α.
Right-tailed test, n=27,α=0.05
Problem 7.5.10
In Exercises 7–12, find the critical value(s) and rejection region(s) for the type of chi-square test with sample size n and level of significance α.
Left-tailed test, n=24,α=0.05
Problem 7.5.11
In Exercises 7–12, find the critical value(s) and rejection region(s) for the type of chi-square test with sample size n and level of significance α.
Two-tailed test, n=81,α=0.10