Back
BackProblem 5.3.24
Finding a z-Score Given an Area In Exercises 23–30, find the indicated z-score.
Find the z-score that has 78.5% of the distribution’s area to its left.
Problem 5.3.27
Finding a z-Score Given an Area In Exercises 23–30, find the indicated z-score.
Find the z-score that has 2.275% of the distribution’s area to its left.
Problem 5.3.30
Finding a z-Score Given an Area In Exercises 23–30, find the indicated z-score.
Find the positive z-score for which 12% of the distribution’s area lies between and z.
Problem 5.3.31c
Finding Specified Data Values In Exercises 31–38, answer the questions about the specified normal distribution.
Weights of Teenagers In a survey of 18-year old males, the mean weight was 166.7 pounds with a standard deviation of 49.3 pounds. (Adapted from National Center for Health Statistics)
c. What weight represents the first quartile?
Problem 5.3.32b
Finding Specified Data Values In Exercises 31–38, answer the questions about the specified normal distribution.
COVID-19 Response Surveyors asked respondents to rate ten key aspects of their government’s response to the COVID-19 pandemic, including preparedness, communication, and material aid. A pandemic response score that ranged from 0 to 100 was calculated. The mean score for U.S. respondents was 50.6 with a standard deviation of 29.0. (Source: PLOS One)
b. What score represents the 61st percentile?
Problem 5.3.33b
Finding Specified Data Values In Exercises 31–38, answer the questions about the specified normal distribution.
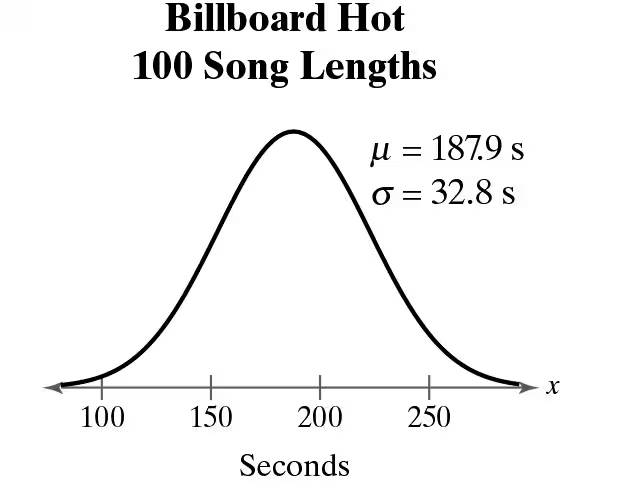
Billboard Hot 100 The length (in seconds) of the 100 most popular songs during the week of May 5, 2021, can be approximated by a normal distribution, as shown in the figure. (Source: Spotify)
b. What song length represents the 17th percentile?
Problem 5.3.35b
Finding Specified Data Values In Exercises 31–38, answer the questions about the specified normal distribution.
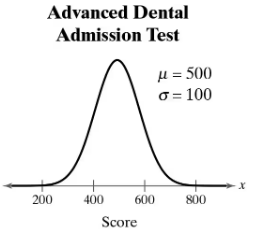
Advanced Dental Admission Test The Advanced Dental Admission Test (ADAT) is designed so that the scores fit a normal distribution, as shown in the figure. (Source: American Dental Association)
b. Between what two values does the middle 50% of the ADAT scores lie?
Problem 5.3.37a
Finding Specified Data Values In Exercises 31–38, answer the questions about the specified normal distribution.
Red Blood Cell Count The red blood cell counts (in millions of cells per microliter) for a population of adult males can be approximated by a normal distribution, with a mean of 5.4 million cells per microliter and a standard deviation of 0.4 million cells per microliter.
a. What is the minimum red blood cell count that can be in the top 25% of counts?
Problem 5.3.39
Bags of Baby Carrots The weights of bags of baby carrots are normally distributed, with a mean of 32 ounces and a standard deviation of 0.36 ounce. Bags in the upper 4.5% are too heavy and must be repackaged. What is the most a bag of baby carrots can weigh and not need to be repackaged?
Problem 5.3.42b
History Grades In a history class, the grades for various assessments are all positive numbers and have different distributions. Determine whether the grades for each assessment could be normally distributed. Explain your reasoning.
b. a final with a mean of 72, standard deviation of 9, and 90th percentile score of 93
Problem 5.3.42e
History Grades In a history class, the grades for various assessments are all positive numbers and have different distributions. Determine whether the grades for each assessment could be normally distributed. Explain your reasoning.
e. an extra credit assignment with a mean of 2.25 and a standard deviation of 2.49
Problem 5.4.40
In Exercises 39 and 40, determine whether the finite correction factor should be used. If so, use it in your calculations when you find the probability.
Old Faithful In a sample of 100 eruptions of the Old Faithful geyser at Yellowstone National Park, the mean interval between eruptions was 129.58 minutes and the standard deviation was 108.54 minutes. A random sample of size 30 is selected from this population. What is the probability that the mean interval between eruptions is between 120 minutes and 140 minutes?
Problem 5.4.38a
Ice Cream The weights of ice cream cartons are normally distributed with a mean weight of 10 ounces and a standard deviation of 0.5 ounce.
a. What is the probability that a randomly selected carton has a weight greater than 10.21 ounces?
Problem 5.4.26
Interpreting the Central Limit Theorem In Exercises 19–26, find the mean and standard deviation of the indicated sampling distribution of sample means. Then sketch a graph of the sampling distribution.
SAT Italian Subject Test The scores on the SAT Italian Subject Test for the 2018–2020 graduating classes are normally distributed, with a mean of 628 and a standard deviation of 110. Random samples of size 25 are drawn from this population, and the mean of each sample is determined.
Problem 5.4.39
In Exercises 39 and 40, determine whether the finite correction factor should be used. If so, use it in your calculations when you find the probability.
Parking Infractions In a sample of 1000 fines issued by the City of Toronto for parking infractions in September of 2020, the mean fine was $49.83 and the standard deviation was $52.15. A random sample of size 60 is selected from this population. What is the probability that the mean fine is less than $40?
Problem 5.4.8
True or False? In Exercises 5–8, determine whether the statement is true or false. If it is false, rewrite it as a true statement.
If the sample size is at least 30, then you can use z-scores to determine the probability that a sample mean falls in a given interval of the sampling distribution.
Problem 5.4.7
True or False? In Exercises 5–8, determine whether the statement is true or false. If it is false, rewrite it as a true statement.
A sampling distribution is normal only when the population is normal.
Problem 5.4.6
True or False? In Exercises 5–8, determine whether the statement is true or false. If it is false, rewrite it as a true statement.
As the sample size increases, the standard deviation of the distribution of sample means increases.
Problem 5.4.5
True or False? In Exercises 5–8, determine whether the statement is true or false. If it is false, rewrite it as a true statement.
As the sample size increases, the mean of the distribution of sample means increases.
Problem 5.4.4
In Exercises 1– 4, a population has a mean mu and a standard deviation sigma. Find the mean and standard deviation of the sampling distribution of sample means with sample size n.
Mu = 1275, sigma =6, n = 1000
Problem 5.4.3
In Exercises 1– 4, a population has a mean mu and a standard deviation sigma. Find the mean and standard deviation of the sampling distribution of sample means with sample size n.
Mu = 790, sigma =48, n = 250
Problem 5.4.2
In Exercises 1– 4, a population has a mean mu and a standard deviation sigma. Find the mean and standard deviation of the sampling distribution of sample means with sample size n.
Mu = 45, sigma =15, n = 100
Problem 5.4.1
In Exercises 1– 4, a population has a mean mu and a standard deviation sigma. Find the mean and standard deviation of the sampling distribution of sample means with sample size n.
Mu = 150, sigma =25, n = 49
Problem 5.4.34
Which Is More Likely? Assume that the fertility rates in Exercise 32 are normally distributed. Are you more likely to randomly select a state with a fertility rate of less than 65 or to randomly select a sample of 15 states in which the mean of the state fertility rates is less than 65? Explain.
Problem 5.4.31
Finding Probabilities for Sampling Distributions In Exercises 29–32, find the indicated probability and interpret the results.
Asthma Prevalence by State The mean percent of asthma prevalence of the 50 U.S. states is 9.51%. A random sample of 30 states is selected. What is the probability that the mean percent of asthma prevalence for the sample is greater than 10%? Assume sigma=1.17%
Problem 5.4.29
Finding Probabilities for Sampling Distributions In Exercises 29–32, find the indicated probability and interpret the results.
Dow Jones Industrial Average From 1975 through 2020, the mean annual gain of the Dow Jones Industrial Average was 652. A random sample of 32 years is selected from this population. What is the probability that the mean gain for the sample was between 400 and 700? Assume sigma=1540
Problem 5.4.18
Finding Probabilities In Exercises 15–18, the population mean and standard deviation are given. Find the indicated probability and determine whether the given sample mean would be considered unusual.
For a random sample of n=36, find the probability of a sample mean being less than 12,750 or greater than 12,753 when mu=12750 and 1.7.
Problem 5.4.17
Finding Probabilities In Exercises 15–18, the population mean and standard deviation are given. Find the indicated probability and determine whether the given sample mean would be considered unusual.
For a random sample of n=45, find the probability of a sample mean being greater than 551 when mu=550 and sigma=3.7.
Problem 5.4.15
Finding Probabilities In Exercises 15–18, the population mean and standard deviation are given. Find the indicated probability and determine whether the given sample mean would be considered unusual.
For a random sample of n=64, find the probability of a sample mean being less than 24.3 when Mu=24 and sigma=1.25.
Problem 5.4.19
Interpreting the Central Limit Theorem In Exercises 19–26, find the mean and standard deviation of the indicated sampling distribution of sample means. Then sketch a graph of the sampling distribution.
Renewable Energy During a recent period of two years, the day-ahead prices for renewable energy in Germany (in euros per mega-watt hour) have a mean of 31.58 and a standard deviation of 12.293. Random samples of size 75 are drawn from this population, and the mean of each sample is determined.