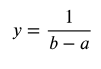Back
BackProblem 5.1.29
Finding Area
In Exercises 23–36, find the indicated area under the standard normal curve. If convenient, use technology to find the area.
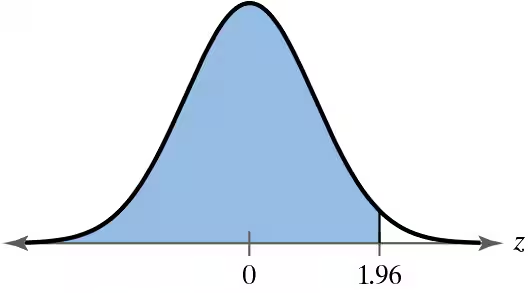
To the right of z= -0.355
Problem 5.1.31
Finding Area
In Exercises 23–36, find the indicated area under the standard normal curve. If convenient, use technology to find the area.
Between z=0 and z=2.86
Problem 5.1.33
Finding Area In Exercises 23–36, find the indicated area under the standard normal curve. If convenient, use technology to find the area.
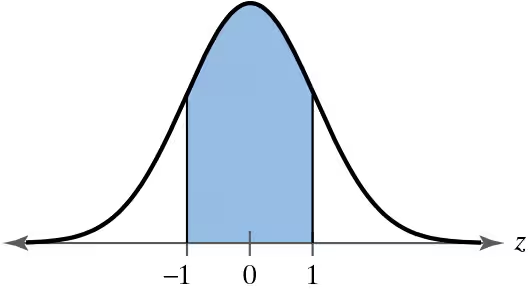
Between z= -1.55 and z= 1.55
Problem 5.1.42
Finding Probability In Exercises 41– 46, find the probability of z occurring in the shaded region of the standard normal distribution. If convenient, use technology to find the probability.
Problem 5.1.45
Finding Probability In Exercises 41– 46, find the probability of z occurring in the shaded region of the standard normal distribution. If convenient, use technology to find the probability.
Problem 5.1.58
Writing Draw a normal curve with a mean of 450 and a standard deviation of 50. Describe how you constructed the curve and discuss its features.
Problem 5.1.60a
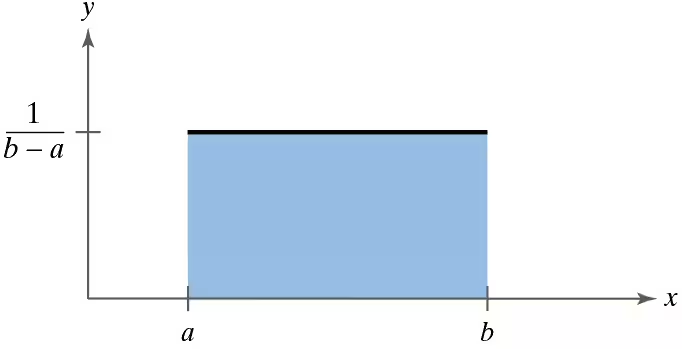
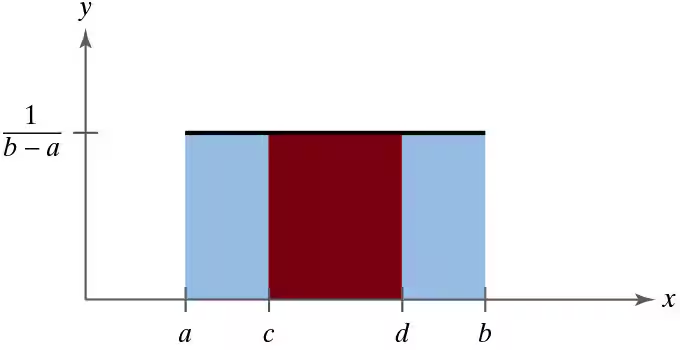
Uniform Distribution A uniform distribution is a continuous probability distribution for a random variable x between two values a and b (a<b), where (a ≤ x ≤ b) and all of the values of x are equally likely to occur. The graph of a uniform distribution is shown below.
The probability density function of a uniform distribution is
on the interval from (x=a) to (x=b). For any value of x less than a or greater than b, y=0 . In Exercises 59 and 60, use this information.
For two values c and d, where a ≤ c < d ≤ b, the probability that x lies between c and d is equal to the area under the curve between c and d, as shown below.
So, the area of the red region equals the probability that x lies between c and d. For a uniform distribution from (a=1) to (b=25) , find the probability that
a. x lies between 2 and 8.
Problem 5.1.60d
Uniform Distribution A uniform distribution is a continuous probability distribution for a random variable x between two values a and b (a<b), where (a ≤ x ≤ b) and all of the values of x are equally likely to occur. The graph of a uniform distribution is shown below.
The probability density function of a uniform distribution is
on the interval from (x=a) to (x=b). For any value of x less than a or greater than b, y=0 . In Exercises 59 and 60, use this information.
For two values c and d, where a ≤ c < d ≤ b, the probability that x lies between c and d is equal to the area under the curve between c and d, as shown below.
So, the area of the red region equals the probability that x lies between c and d. For a uniform distribution from (a=1) to (b=25) , find the probability that
d. x lies between 8 and 14.
Problem 5.2.9a
Finding Probabilities for Normal Distributions In Exercises 7–12, find the indicated probabilities. If convenient, use technology to find the probabilities.
MCAT Scores In a recent year, the MCAT total scores were normally distributed, with a mean of 500.9 and a standard deviation of 10.6. Find the probability that a randomly selected medical student who took the MCAT has a total score that is (a) less than 490. Identify any unusual events in parts (a)–(c). Explain your reasoning. (Source: Association of American Medical Colleges)
Problem 5.2.12a
Finding Probabilities for Normal Distributions In Exercises 7–12, find the indicated probabilities. If convenient, use technology to find the probabilities.
Health Club Schedule The amounts of time per workout an athlete uses a stairclimber are normally distributed, with a mean of 20 minutes and a standard deviation of 5 minutes. Find the probability that a randomly selected athlete uses a stairclimber for (a) less than 17 minutes.
Problem 5.2.15
Graphical Analysis In Exercises 13–16, a member is selected at random from the population represented by the graph. Find the probability that the member selected at random is from the shaded region of the graph. Assume the variable x is normally distributed.
Problem 5.2.9b
Finding Probabilities for Normal Distributions In Exercises 7–12, find the indicated probabilities. If convenient, use technology to find the probabilities.
MCAT Scores In a recent year, the MCAT total scores were normally distributed, with a mean of 500.9 and a standard deviation of 10.6. Find the probability that a randomly selected medical student who took the MCAT has a total score that is (b) between 490 and 510. Identify any unusual events in parts (a)–(c). Explain your reasoning. (Source: Association of American Medical Colleges)
Problem 5.2.9c
Finding Probabilities for Normal Distributions In Exercises 7–12, find the indicated probabilities. If convenient, use technology to find the probabilities.
MCAT Scores In a recent year, the MCAT total scores were normally distributed, with a mean of 500.9 and a standard deviation of 10.6. Find the probability that a randomly selected medical student who took the MCAT has a total score that is (c) more than 515. Identify any unusual events in parts (a)–(c). Explain your reasoning. (Source: Association of American Medical Colleges)
Problem 5.2.12b
Finding Probabilities for Normal Distributions In Exercises 7–12, find the indicated probabilities. If convenient, use technology to find the probabilities.
Health Club Schedule The amounts of time per workout an athlete uses a stairclimber are normally distributed, with a mean of 20 minutes and a standard deviation of 5 minutes. Find the probability that a randomly selected athlete uses a stairclimber for (b) between 20 and 28 minutes.
Problem 5.2.12c
Finding Probabilities for Normal Distributions In Exercises 7–12, find the indicated probabilities. If convenient, use technology to find the probabilities.
Health Club Schedule The amounts of time per workout an athlete uses a stairclimber are normally distributed, with a mean of 20 minutes and a standard deviation of 5 minutes. Find the probability that a randomly selected athlete uses a stairclimber for (c) more than 30 minutes.
Problem 5.2.3
Computing Probabilities for Normal Distributions In Exercises 1–6, the random variable x is normally distributed with mean mu=174 and standard deviation sigma=20. Find the indicated probability.
P(x > 182)
Problem 5.2.6
Computing Probabilities for Normal Distributions In Exercises 1–6, the random variable x is normally distributed with mean mu=174 and standard deviation sigma=20. Find the indicated probability.
P(172 < x <192)
Problem 5.2.17b
SAT Total Scores Use the normal distribution in Exercise 13.
b. Out of 1000 randomly selected SAT total scores, about how many would you expect to be greater than 1100?
Problem 5.2.19a
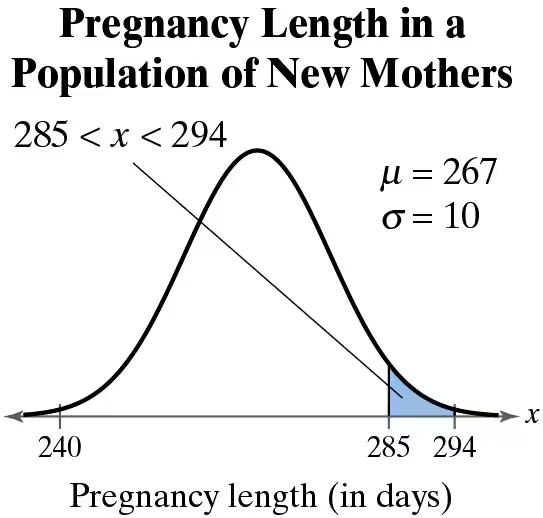
Pregnancy Length Use the normal distribution in Exercise 15.
a. What percent of the new mothers had a pregnancy length of less than 290 days?
Problem 5.2.20a
Red Blood Cell Count Use the normal distribution in Exercise 16.
a. What percent of the adult males have a red blood cell count less than 6 million cells per microliter?
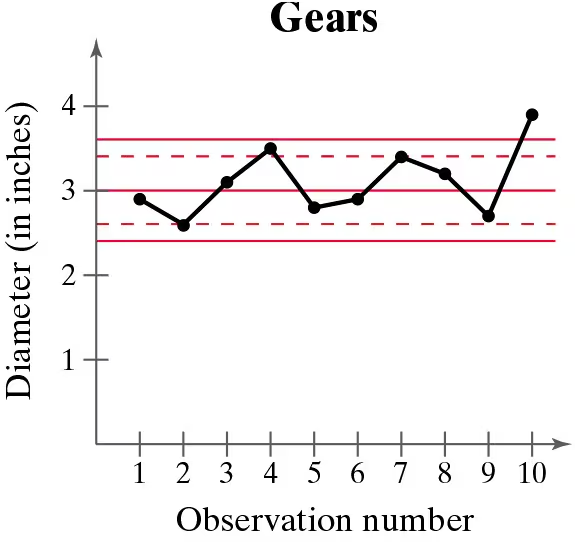
Problem 5.2.21
In Exercises 21–24, a control chart is shown. Each chart has horizontal lines drawn at the mean mu, at mu ±2sigma, and at mu±3sigma. Determine whether the process shown is in control or out of control. Explain.
A gear has been designed to have a diameter of 3 inches. The standard deviation of the process is 0.2 inch.
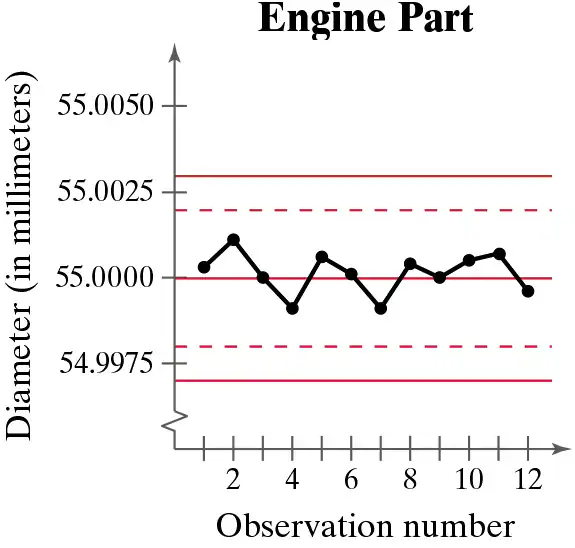
Problem 5.2.24
In Exercises 21–24, a control chart is shown. Each chart has horizontal lines drawn at the mean mu, at mu ±2sigma, and at mu±3sigma. Determine whether the process shown is in control or out of control. Explain.
An engine part has been designed to have a diameter of 55 millimeters. The standard deviation of the process is 0.001 millimeter.
Problem 5.3.34b
Finding Specified Data Values In Exercises 31–38, answer the questions about the specified normal distribution.
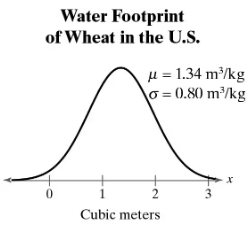
Water Footprint A water footprint is a measure of the appropriation of fresh water. The water footprint (in cubic meters) for a kilogram of wheat can be approximated by a normal distribution, as shown in the figure. (Source: Ecological Indicators)
b. What water footprint represents the 29th percentile?
Problem 5.3.3
Finding a z-Score In Exercises 1–16, use the Standard Normal Table or technology to find the z-score that corresponds to the cumulative area or percentile.
0.6736
Problem 5.3.6
Finding a z-Score In Exercises 1–16, use the Standard Normal Table or technology to find the z-score that corresponds to the cumulative area or percentile.
0.94
Problem 5.3.9
Finding a z-Score In Exercises 1–16, use the Standard Normal Table or technology to find the z-score that corresponds to the cumulative area or percentile.
P33
Problem 5.3.12
Finding a z-Score In Exercises 1–16, use the Standard Normal Table or technology to find the z-score that corresponds to the cumulative area or percentile.
P1.5
Problem 5.3.15
Finding a z-Score In Exercises 1–16, use the Standard Normal Table or technology to find the z-score that corresponds to the cumulative area or percentile.
P91
Problem 5.3.18
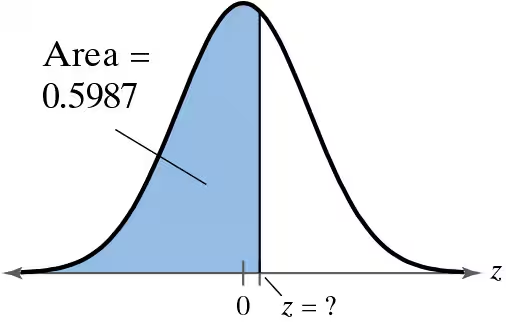
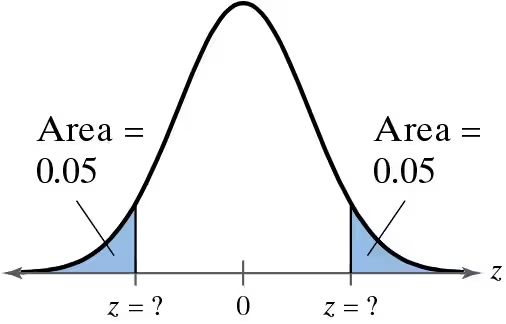
Graphical Analysis In Exercises 17–22, find the indicated z-score(s) shown in the graph.
Problem 5.3.21
Graphical Analysis In Exercises 17–22, find the indicated z-score(s) shown in the graph.